平行四边形的认识复习
图片预览

文档简介
《平行四边形的认识》小结与复习
学习目标:
通过本章内容的回顾与梳理,使学生对所学知识进行系统复习与归纳。
了解四边形、特殊四边形的关系及转化条件,在交流反思的过程中逐渐建立知识体系。
在观察、操作、推理、归纳探索中发展合情推理能力,培养说理习惯与能力。
学习过程:
创设情境、导入新课:
同学们在拍照留念的时候最喜欢做一个“V”字型的动作。我们将宽为的长方形如图进行翻折,便可得到一个漂亮的“V”.如果“V”所成的锐角为600,那么折痕PQ的长是
整合拓展、探究创新
(一)、平行四边形
1.定义:两组对边分别平行的四边形。
2.性质:对边______,对角______,对角线_____________,对称性_________。
3.能力体现:
①(2011湖南)如图,□ABCD中,对角线AC,BD相
交于点O,且AB≠AD,则下列式子不正确的是( )
A.AC⊥BD B.AB=CD
C. BO=OD D.∠BAD=∠BCD
②(2012广西)如图,□ABCD中,AC、BD为对角线,
BC=6,BC边上的高为4,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
③□ABCD的周长为60cm,对角线交于点O,△BOC的周长
比△AOB的周长少8cm,则AB、BC的长分别为( )
A.18cm 20cm B.20cm 12cm C.34cm 26cm D.19cm 11cm
(二)、矩形
1.定义:有一个角是________的平行四边形。
2.性质:对边___________,四个角____________,对角线____________________,对称性________________。
3.能力体现:
①(2012年长沙)如图,矩形的两条对角
线相交于点,,则矩形的对
角线的长是( )
A.2 B.4 C. D.
②(2011湖北)如图:矩形ABCD的对角线AC=10,BC=8,
则图中五个小矩形的周长之和为_______.
③矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边
与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
(三)、菱形
1.定义:有________________的平行四边形。
2.性质:四条边___________,对边________, 对角____________,对角线_____________________________,对称性_______________________。
3.能力体现:
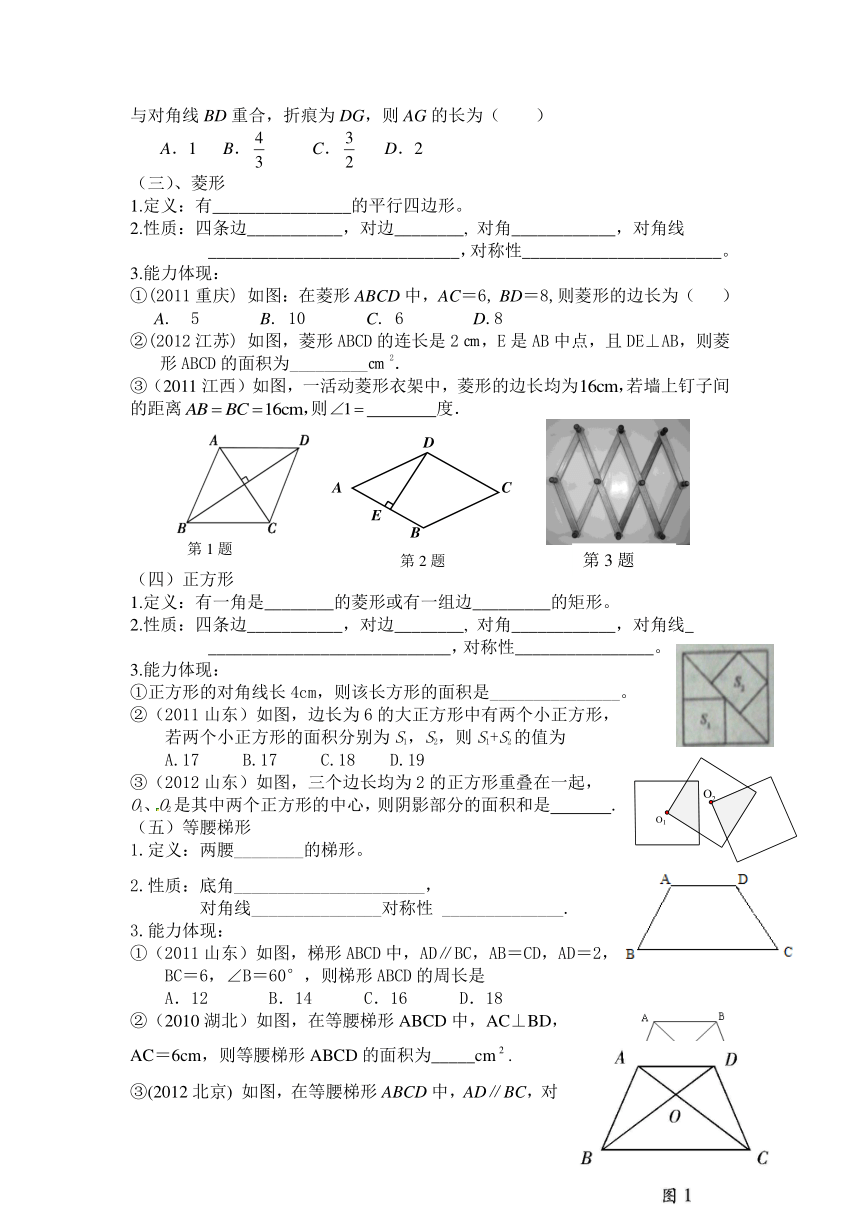
①(2011重庆) 如图:在菱形ABCD中,AC=6, BD=8,则菱形的边长为( )
A. 5 B. 10 C. 6 D.8
②(2012江苏) 如图,菱形ABCD的连长是2㎝,E是AB中点,且DE⊥AB,则菱形ABCD的面积为_________㎝2.
③(2011江西)如图,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距离则 度.
(四)正方形
1.定义:有一角是________的菱形或有一组边_________的矩形。
2.性质:四条边___________,对边________, 对角____________,对角线_ ____________________________,对称性________________。
3.能力体现:
①正方形的对角线长4cm,则该长方形的面积是_______________。
②(2011山东)如图,边长为6的大正方形中有两个小正方形,
若两个小正方形的面积分别为S1,S2,则S1+S2的值为
A.17 B.17 C.18 D.19
③(2012山东)如图,三个边长均为2的正方形重叠在一起,
O1、O2是其中两个正方形的中心,则阴影部分的面积和是 .
(五)等腰梯形
1.定义:两腰________的梯形。
2.性质:底角______________________,
对角线_______________对称性 ______________.
3.能力体现:
①(2011山东)如图,梯形ABCD中,AD∥BC,AB=CD,AD=2,BC=6,∠B=60°,则梯形ABCD的周长是
A.12 B.14 C.16 D.18
②(2010湖北)如图,在等腰梯形ABCD中,AC⊥BD,
AC=6cm,则等腰梯形ABCD的面积为_____cm.
③(2012北京) 如图,在等腰梯形ABCD中,AD∥BC,对 角线AC、BD相交于点O,以下四个结论:① ,②OA=OD ,③,④S=S,其中正确的是( )
A. ①② B.①④
C.②③④ D.①②④
应用实践、拓展提高
① (2012年义乌)如图,一块砖的外侧面积为,那么图中残留部分墙面的面积为( )
A. B. C. D.
②(2011浙江)新农村建设推动了农村住宅旧貌变新颜,如图为一农村民居侧面截图,屋坡分别架在墙体的点、点处,且,侧面四边形为矩形,若测得,则( )
A. 35° B. 40° C. 55° D. 70°
总结反思、归纳升华
收获与疑_____________________________________________。
达标检测、体验成功(每题4分,共20分)
①.(2011江苏)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于___________.
②.(2012山东)已知一个菱形的周长是20cm,两条对角线的比是4∶3,则这个菱形的面积是( )
A.12cm2 B. 24cm2 C. 48cm2 D. 96cm2
③.(2011湖南)下列四边形中,对角线相等且互相垂直平分的是( )
A.菱形 B.正方形 C.等腰梯形 D.矩形
⑤.下列图形中:①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形.其中既是中心对称图形又是轴对称图形的共有( )个.
A、1 B、2 C、3 D、4
⑥.如图,在等腰梯形ABCD中,AD∥BC,∠B=45°,AE⊥BC,且AE=AD=2cm,求这个梯形的面积.
阅读材料
四边形的变身术
我们知道,一个平行四边形总可以剪开拼成一个矩形.
一个梯形可以剪开拼成一个矩形,一个矩形可以剪开拼成一个三角形.
那么任意一个四边形呢?它也可以剪开拼成各种各样的图形.下面给出了一些剪拼的示意图,观察一下,你也试试看.
想想看,在这些剪拼过程中,都用到了图形的什么变换?
学习目标:
通过本章内容的回顾与梳理,使学生对所学知识进行系统复习与归纳。
了解四边形、特殊四边形的关系及转化条件,在交流反思的过程中逐渐建立知识体系。
在观察、操作、推理、归纳探索中发展合情推理能力,培养说理习惯与能力。
学习过程:
创设情境、导入新课:
同学们在拍照留念的时候最喜欢做一个“V”字型的动作。我们将宽为的长方形如图进行翻折,便可得到一个漂亮的“V”.如果“V”所成的锐角为600,那么折痕PQ的长是
整合拓展、探究创新
(一)、平行四边形
1.定义:两组对边分别平行的四边形。
2.性质:对边______,对角______,对角线_____________,对称性_________。
3.能力体现:
①(2011湖南)如图,□ABCD中,对角线AC,BD相
交于点O,且AB≠AD,则下列式子不正确的是( )
A.AC⊥BD B.AB=CD
C. BO=OD D.∠BAD=∠BCD
②(2012广西)如图,□ABCD中,AC、BD为对角线,
BC=6,BC边上的高为4,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
③□ABCD的周长为60cm,对角线交于点O,△BOC的周长
比△AOB的周长少8cm,则AB、BC的长分别为( )
A.18cm 20cm B.20cm 12cm C.34cm 26cm D.19cm 11cm
(二)、矩形
1.定义:有一个角是________的平行四边形。
2.性质:对边___________,四个角____________,对角线____________________,对称性________________。
3.能力体现:
①(2012年长沙)如图,矩形的两条对角
线相交于点,,则矩形的对
角线的长是( )
A.2 B.4 C. D.
②(2011湖北)如图:矩形ABCD的对角线AC=10,BC=8,
则图中五个小矩形的周长之和为_______.
③矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边
与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
(三)、菱形
1.定义:有________________的平行四边形。
2.性质:四条边___________,对边________, 对角____________,对角线_____________________________,对称性_______________________。
3.能力体现:
①(2011重庆) 如图:在菱形ABCD中,AC=6, BD=8,则菱形的边长为( )
A. 5 B. 10 C. 6 D.8
②(2012江苏) 如图,菱形ABCD的连长是2㎝,E是AB中点,且DE⊥AB,则菱形ABCD的面积为_________㎝2.
③(2011江西)如图,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距离则 度.
(四)正方形
1.定义:有一角是________的菱形或有一组边_________的矩形。
2.性质:四条边___________,对边________, 对角____________,对角线_ ____________________________,对称性________________。
3.能力体现:
①正方形的对角线长4cm,则该长方形的面积是_______________。
②(2011山东)如图,边长为6的大正方形中有两个小正方形,
若两个小正方形的面积分别为S1,S2,则S1+S2的值为
A.17 B.17 C.18 D.19
③(2012山东)如图,三个边长均为2的正方形重叠在一起,
O1、O2是其中两个正方形的中心,则阴影部分的面积和是 .
(五)等腰梯形
1.定义:两腰________的梯形。
2.性质:底角______________________,
对角线_______________对称性 ______________.
3.能力体现:
①(2011山东)如图,梯形ABCD中,AD∥BC,AB=CD,AD=2,BC=6,∠B=60°,则梯形ABCD的周长是
A.12 B.14 C.16 D.18
②(2010湖北)如图,在等腰梯形ABCD中,AC⊥BD,
AC=6cm,则等腰梯形ABCD的面积为_____cm.
③(2012北京) 如图,在等腰梯形ABCD中,AD∥BC,对 角线AC、BD相交于点O,以下四个结论:① ,②OA=OD ,③,④S=S,其中正确的是( )
A. ①② B.①④
C.②③④ D.①②④
应用实践、拓展提高
① (2012年义乌)如图,一块砖的外侧面积为,那么图中残留部分墙面的面积为( )
A. B. C. D.
②(2011浙江)新农村建设推动了农村住宅旧貌变新颜,如图为一农村民居侧面截图,屋坡分别架在墙体的点、点处,且,侧面四边形为矩形,若测得,则( )
A. 35° B. 40° C. 55° D. 70°
总结反思、归纳升华
收获与疑_____________________________________________。
达标检测、体验成功(每题4分,共20分)
①.(2011江苏)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于___________.
②.(2012山东)已知一个菱形的周长是20cm,两条对角线的比是4∶3,则这个菱形的面积是( )
A.12cm2 B. 24cm2 C. 48cm2 D. 96cm2
③.(2011湖南)下列四边形中,对角线相等且互相垂直平分的是( )
A.菱形 B.正方形 C.等腰梯形 D.矩形
⑤.下列图形中:①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形.其中既是中心对称图形又是轴对称图形的共有( )个.
A、1 B、2 C、3 D、4
⑥.如图,在等腰梯形ABCD中,AD∥BC,∠B=45°,AE⊥BC,且AE=AD=2cm,求这个梯形的面积.
阅读材料
四边形的变身术
我们知道,一个平行四边形总可以剪开拼成一个矩形.
一个梯形可以剪开拼成一个矩形,一个矩形可以剪开拼成一个三角形.
那么任意一个四边形呢?它也可以剪开拼成各种各样的图形.下面给出了一些剪拼的示意图,观察一下,你也试试看.
想想看,在这些剪拼过程中,都用到了图形的什么变换?
