华东师大版八年级下册数学 19.1.2 矩形的判定 课件 (共17张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.1.2 矩形的判定 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 218.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
矩形的判定
【复习提问】
1.什么叫做矩形?
2.矩形有哪些特征?
【思考与探究】
如何判定一个四边形是不是矩形呢?
你知道如何判定一个平行四边形是矩形吗?
一个角是直角
平行四边形
矩形
情境一
李芳同学用画“边—直角、边——直角、
边——直角、边“这样四步画出了一个四边
形;她说这就是矩形,她的判断正确吗?
为什么?
猜想:有三个角是直角的四边形是矩形
你能证明上述结论吗?
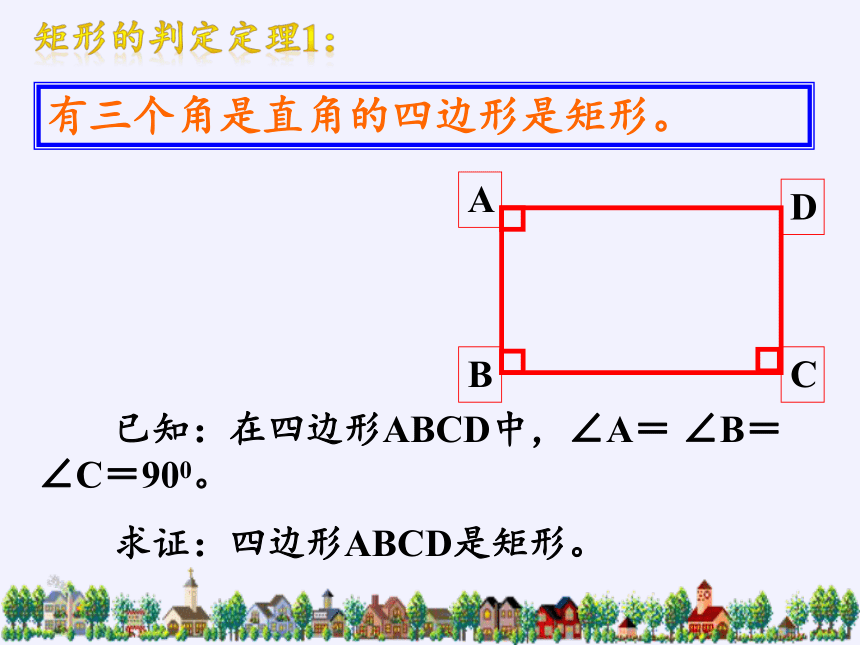
有三个角是直角的四边形是矩形。
A
B
D
C
已知:在四边形ABCD中,∠A= ∠B= ∠C=900。
求证:四边形ABCD是矩形。
矩形的判定定理1:
情境二:木工师傅检查所做的门窗是否是矩形常用什么方法?为什么?
答:木工师傅靠测量门窗的对角线是否相等来判断所做的门窗是否是矩形。因为对角线相等的平行四边形是矩形。
对角线相等的平行四边形是矩形。
A
B
D
C
已知:在 ABCD中,AC= BD。
求证:四边形ABCD是矩形。
矩形的判定定理2:
有一个角是直角的平行四边形是矩形。
矩形的判定:
定义
有三个角是直角的四边形是矩形。
矩形判定定理1
对角线相等的平行四边形是矩形。
矩形判定定理2
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
例1:已知M为 ABCD的AD边的中点,且MB=MC。求证: ABCD是矩形。
A
B
D
C
M
证明:
∵ABCD是平行四边形
∵M是AD的中点
∴AM=DM
∵ MB=MC
∴△BAM≌ △CDM
∴∠A= ∠D
∴ AB∥CD AB=CD
∴ ∠A+ ∠D=1800
∴∠A= 900
∴ ABCD是矩形
例2:延长Rt△ABC斜边上的中线CE到D,使DE=CE。求证:四边形ACBD是矩形。
A
C
B
E
D
分析:要证四边形ACBD是矩形,已经有一个直角的条件,若能证它是平行四边形就可以了。
巩固练习1.
1.已知:如图, ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
2.已知:如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,求证四边形EFGH是矩形.
拓展提升
如图,△ABC中,点O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F, (1)求证:OE=OF; (2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论。
课堂小结:
谈谈你本节课的收获
布置作业
教材P106页 2题
107页3,5题
谢 谢
矩形的判定
【复习提问】
1.什么叫做矩形?
2.矩形有哪些特征?
【思考与探究】
如何判定一个四边形是不是矩形呢?
你知道如何判定一个平行四边形是矩形吗?
一个角是直角
平行四边形
矩形
情境一
李芳同学用画“边—直角、边——直角、
边——直角、边“这样四步画出了一个四边
形;她说这就是矩形,她的判断正确吗?
为什么?
猜想:有三个角是直角的四边形是矩形
你能证明上述结论吗?
有三个角是直角的四边形是矩形。
A
B
D
C
已知:在四边形ABCD中,∠A= ∠B= ∠C=900。
求证:四边形ABCD是矩形。
矩形的判定定理1:
情境二:木工师傅检查所做的门窗是否是矩形常用什么方法?为什么?
答:木工师傅靠测量门窗的对角线是否相等来判断所做的门窗是否是矩形。因为对角线相等的平行四边形是矩形。
对角线相等的平行四边形是矩形。
A
B
D
C
已知:在 ABCD中,AC= BD。
求证:四边形ABCD是矩形。
矩形的判定定理2:
有一个角是直角的平行四边形是矩形。
矩形的判定:
定义
有三个角是直角的四边形是矩形。
矩形判定定理1
对角线相等的平行四边形是矩形。
矩形判定定理2
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
例1:已知M为 ABCD的AD边的中点,且MB=MC。求证: ABCD是矩形。
A
B
D
C
M
证明:
∵ABCD是平行四边形
∵M是AD的中点
∴AM=DM
∵ MB=MC
∴△BAM≌ △CDM
∴∠A= ∠D
∴ AB∥CD AB=CD
∴ ∠A+ ∠D=1800
∴∠A= 900
∴ ABCD是矩形
例2:延长Rt△ABC斜边上的中线CE到D,使DE=CE。求证:四边形ACBD是矩形。
A
C
B
E
D
分析:要证四边形ACBD是矩形,已经有一个直角的条件,若能证它是平行四边形就可以了。
巩固练习1.
1.已知:如图, ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
2.已知:如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,求证四边形EFGH是矩形.
拓展提升
如图,△ABC中,点O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F, (1)求证:OE=OF; (2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论。
课堂小结:
谈谈你本节课的收获
布置作业
教材P106页 2题
107页3,5题
谢 谢
