2021-2022学年人教版数学九年级下册28.1锐角三角函数课后提升(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册28.1锐角三角函数课后提升(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 652.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 19:21:56 | ||
图片预览




文档简介
锐角三角函数
一、单选题
1.如图,在中,,则等于( )
A. B. C. D.
2.在下列网格中,小正方形的边长为1,点A,B,求∠A的余弦值( )
A. B. C. D.
3.如果∠A为锐角,cosA=,那么∠A 取值范围是( )
A.0°<∠A≤30° B.30°<∠A≤45° C.45°<∠A<60° D.60°<∠A<90°
4.如图,已知中,,,若,于点E,则( )
A. B. C. D.
5.如图,矩形ABCD中,AD=4,AB=5,E是AB边上的一点,连接DE、EC.若EC平分∠BED,则sin∠BCE的值是( )
A. B. C. D.
6.如图,菱形OABC的边OC在轴上,点A、B在第一象限内,,反比例函数的图象经过点A,若菱形的面积为4,则的值为( )
A.1 B.2 C.3 D.4
7.如图,在矩形ABCD中,AD=2,AB=1,以A为圆心,AD的长为半径画弧交BC于点E,则图中空白部分的面积是( )
A.1﹣ B.2﹣ C. D.2+
8.如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A. B. C. D.
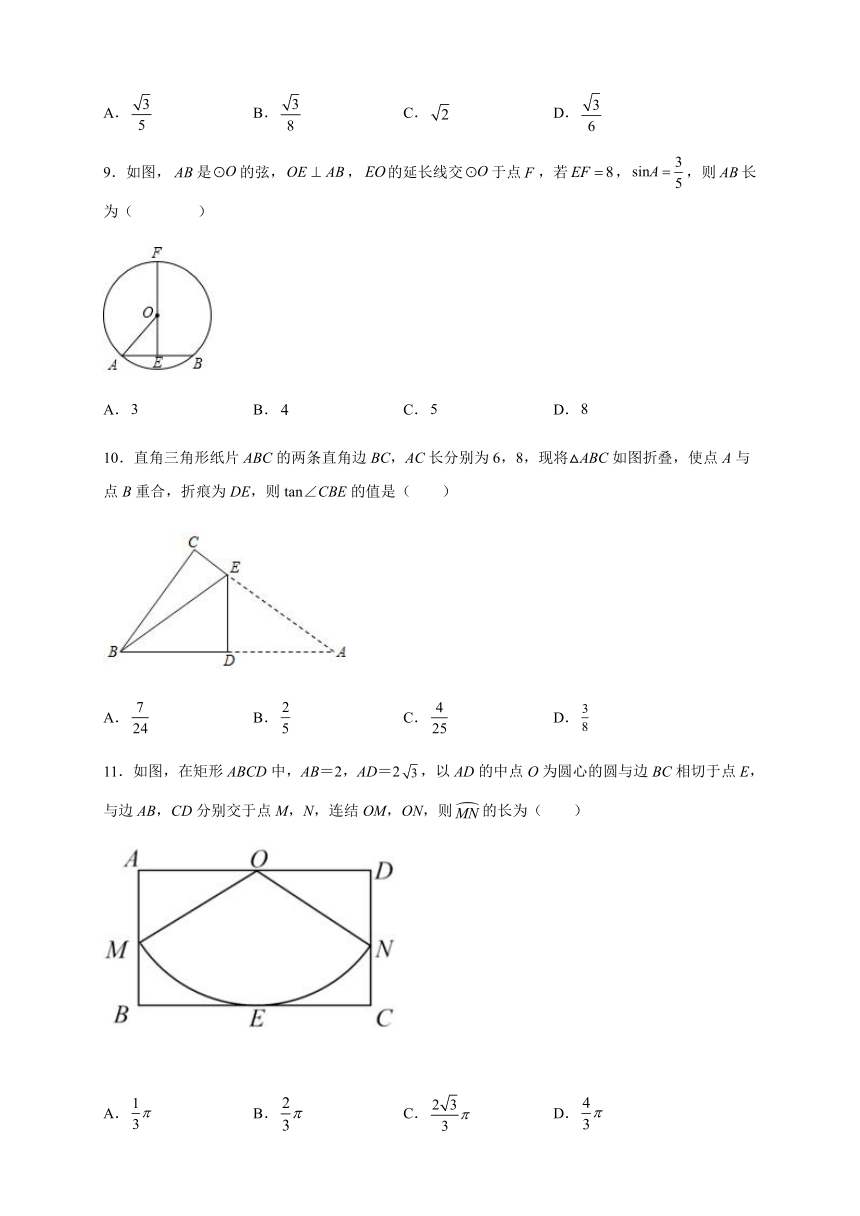
9.如图,是的弦,,的延长线交于点,若,,则长为( )
A. B. C. D.
10.直角三角形纸片ABC的两条直角边BC,AC长分别为6,8,现将△ABC如图折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
11.如图,在矩形ABCD中,AB=2,AD=2,以AD的中点O为圆心的圆与边BC相切于点E,与边AB,CD分别交于点M,N,连结OM,ON,则的长为( )
A. B. C. D.
12.如图,A、B分别为反比例函数(x<0),y=(x>0)图象上的点,且OA⊥OB,则tan∠ABO的值为( )
A. B. C. D.
13.如图,正方形ABCD中,E、F分别为BC、CD边上的点,∠EAF=45°,则下列结论中正确的有( )
①BE+DF=EF;
②tan∠AMD=;
③BM2+DN2=MN2;
④若EF=1.5,△AEF的面积是3,则正方形ABCD的面积是4.
A.1个 B.2个 C.3个 D.4个
14.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE、AF,DE与AF交于点O.连接OC,则OC的值为( )
A. B.1 C. D.
15.如图,AB是半圆的直径,AC是一条弦,D是的中点,于点E,DE交AC于点F,DB交AC于点G,,则的值为( )
A. B. C. D.
二、填空题
16.计算:的结果为______.
17.若为锐角,已知,那么______°.
18.在矩形ABCD中,BC=2AB,点P在直线BC上,且PC=AB,则∠APB的正切值为_____.
19.已知,中,是锐角,,则的度数是__________.
20.小明沿着坡度为1∶的山坡走了100m,则他升高了______米.
三、解答题
21.计算:
(1)sin60° cos30°﹣1 (2)2sin30°+3cos60°﹣4tan45°
(3) (4)2tan60°+tan45°﹣4cos30°
22.先化简,再求值:
(1)÷(﹣a+2),其中a=2sin60°﹣3tan45°.
(2),其中x=2+tan30°.
23.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,且∠A,∠B都是锐角,求∠C的度数.
24.如图,点C是直径AB上一点.过C作交于点D,连接DA,DB.
(1)求证:;
(2)连接DO,过点D做的切线,交BA的延长线于点P.若,,求BC的长.
25.如图1,反比例函数y=的图象经过A(1,m)、B(2,1)两点,点P的坐标为(6,1).
(1)求反比例函数的表达式;
(2)连接PA、PB,求tan∠P的值;
(3)如图2,点C、D的坐标是(a,0)、(0,a)(0<a≤6),当△PCD的面积为3时,求a的值.
试卷第1页,共3页
参考答案:
1.B
解:解:由图可知, =
故答案选:B
2.C
解:点C如图所示:
AO==2,
cos∠A===,
故选:C.
3.C
解:∵cos60°=,cos45°=,且
∴45°<∠A<60°.
故选C.
4.D
解:连接AD,如图所示:
∵,BD=DC,
∴AD⊥BC,
∵,
∴,
∴,即,
∵,,
∴,
∴在Rt△ADB中,,
∴;
故选D.
5.A
解:四边形是矩形,,
,
,
平分,
,
,
,
,
,
,
,
故选:A.
6.B
解:过点A作AD⊥x轴于D,设菱形OABC的边长为x,
∵,
∴AD=OAsin∠AOC=,OD=OAcos∠AOC=,
∵菱形的面积为4,
∴OC·AD=,
∴k=xy=OD·AD=,
故选择B.
7.B
解:∵四边形ABCD是矩形,
∴∠B=90°,AD∥CB,
∵AB=1,AE=AD=2,
∴AE=2AB,
∴∠AEB=30°,
∴∠DAE=∠AEB=30°,
∴S阴==,
则图中空白部分的面积是
故选:B.
8.A
解:作于,
四边形是平行四边形,
.
.
是角平分线,
.
.
.
同理.
.
四边形是平行四边形.
,
四边形是菱形.
,,
,,,
,
,,
.
故选:A.
9.D
解:在中,,
::,
::,
,
,,
由勾股定理得,,
,
,
故选:D.
10.A
解:设CE=x,则AE=8﹣x,
∵△ABC如图折叠,使点A与点B重合,
∴BE=AE=8﹣x,
Rt△BCE中,CE2+BC2=BE2,
∴x2+62=(8﹣x)2,
解得x= ,
Rt△BCE中,
tan∠CBE=,
故选:A.
11.D
解:如图,连接OE,
∵⊙O与边BC相切于点E,
∴BC⊥OE,
∴∠OEB=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴四边形AOEB是矩形,
∵OE=AB=2,
∴OM=ON=OE=2,
∵AD=2,O为AD的中点,
∴OA=AD=×2=,
∴cos∠AOM==,
∴∠AOM=30°,
∵∠A=∠D=90°,OM=ON,OA=OD,
∴Rt△AOM≌Rt△DON(HL),
∴∠AOM=∠DON=30°,
∴∠MON=180°﹣30°﹣30°=120°,
∴l==π,
∴的长为π.
故选:D
12.A
解:如图,过A作AC⊥x轴于C,过B作BD⊥x轴于D
则∠BDO=∠ACO=90°
∵A、B分别为反比例函数(x<0),(x>0)图象上的点
∴S△AOC=4,S△BDO=9
∵∠AOB=90°
∴∠BOD+∠DBO=∠BOD+∠AOC=90°
∴∠DBO=∠AOC
∴△BDO∽△OCA
∴
∴
∴
故选:A.
13.C
解: ∵四边形ABCD为正方形,
∴AD=AB,∠ADF=90°,∠ABC=90°,
将△ADF顺时针旋转90°得到△ABF′,
∴AF=AF′,DF=BF′,∠DAF=∠BAF′,∠ADF=∠ADF′=90°,
∴∠F′BE=∠ABF′+∠ABE=90°+90°=180°,
∵∠BAE+∠DAF=90°-∠EAF=90°-45°=45°,
∴∠F′AE=∠FAB+∠BAE=∠DAF+∠BAE=45°=∠FAE,
在△AF′E和△AFE中,
,
∴△AF′E≌△AFE(SAS),
∴F′E=FE,
∴BE+DF=BE+BF′=F′E=EF,
故①正确;
∵BD为正方形的对角线,
∴∠ABM=∠FDN=45°=∠MAN,
∵∠ANM=∠DNF,
∴∠AMN=180°-∠MAN-∠ANM=180°-∠NDF-∠DNF=∠DFN,
∴tan∠AMN=tan∠DFA=,
故②正确;
将△AND顺时针旋转90°得到△ABN′,连结N′M,
∴AN=AN′,∠AND=∠ABN′=45°,DN=BN′,
∵∠N′AM=∠NAB+∠BAE=∠DAF+∠BAE=45°=∠NAM,
在△AN′M和△ANM中,
,
∴△AN′M≌△ANM(SAS),
∴N′M=NM,
∵∠N′BM=∠ABN′+∠ABM=45°+45°=90°,
∴根据勾股定理,即,
故③正确;
∵S△AEF=S△AF′E=3,F′E=FE=1.5,
∴,即,
∴AB=4,
∴S正方形ABCD=AB2=16,
故④不正确.
故选C.
14.B
解:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠DAE=90°,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAD=∠BAF+∠DAO=90°,
∴∠ADE+∠DAO=90°,
∴∠AOD=90°,
∵E、F分别为AB,BC的中点,
∴AE=AB,BF=BC,
∵AB=BC,
∴AE=BF,
过C作CG⊥DE于G,
∵∠OAD+∠ADO=∠ADO+∠CDG=90°,
∴∠OAD=∠CDG,
在△ADO和△DCG中,
,
∴△ADO≌△DCG(AAS),
∴AO=DG,
∵,
∴DO=2AO=2DG,
∴DG=OG,
∴CG为DO的垂直平分线,
∴OC=DC=1,
故选:B.
15.C
解:连接AD,BC,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠ADE+∠EDB=90°,
又∵DE⊥AB,
∴∠EDB+∠ABD=90°,
∴∠ADE=∠ABD,
∵D是的中点,
∴∠DAC=∠ABD,
∴∠ADE=∠DAC,
∴FA=FD;
∵∠ADE=∠DBC,∠ADE+∠EDB=90°,∠DBC+∠CGB=90°,
∴∠EDB=∠CGB,
又∵∠DGF=∠CGB,
∴∠EDB=∠DGF,
∴FD=FG,
∴FA=FD=FG,
∵在Rt△AEF中,,
∴设EF=3k,AE=4k,则AF=DF=FG=5k,AG=10k,DE=8k,
在Rt△ADE中,,
∵AB是直径,
∴∠ADG=∠GCB=90°,
∵∠AGD=∠CGB,
∴cos∠CGB=cos∠AGD,
∴,
在Rt△ADG中,,
∴,
故选:C.
16.
解:原式
,
故答案为:.
17.60
解:由为锐角,且,那么等于,
故填:60.
18.1或##或1
解:(1)如图①所示,
BC=2AB,PC=AB,
∴P是BC的中点,即BP=PC,
又∵四边形ABCD是矩形,
∴tan∠APB==1;
(2)如图②所示,
∵BC=2AB.PC=AB,
∴BP=3AB,
∴tan∠APB==.
综上所述∠APB的正切值为1或.
故答案为1或.
19.
解:∵中,是锐角,,
∴∠A=30°.
故答案为30°.
20.50
解:设升高了xm,根据坡比为1:,则可得水平距离为xm,
∴由勾股定理得x2+(x)2=1002,
解得x=50,x=-50(舍去),
故答案为50.
21.(1) (2) (3) (4)1
(1)
解:原式=
=
=;
(2)
原式=
=
=
(3)
解:
=
=
=
(4)
解:2tan60°+tan45°﹣4cos30°
=
=
=1
22.(1) (2);
(1)解:原式=
∵a=2sin60°-3tan45°
∴a=,
∴ 原式
(2)解:
原式
23.∠C=90°.
解:∵|sinA﹣|+(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,cosB=,
∴∠A=45°,∠B=45°,
∴∠C=180°﹣45°﹣45°=90°.
24.(1)见详解;
(2)240.
(1)
证明:∵为的直径
∴,
∵
∴
∴
(2)
解:∵为的切线
∴
∴
∵
∴
∵
∴
设,,则
∴,,
∴
∵
∴
∴
∴
25.(1)y=
(2)
(3)1或6
(1)
∵反比例函数y=的图象经过B(2,1)点,
∴k=2×1=2,
∴反比例函数的关系式为y=;
(2)
∵反比例函数y=的图象经过A(1,m)、
∴m=2,
∴A(1,2),
过点A作BP的垂线,交PB的延长线于点M,
则AM=2﹣1=1,MP=6﹣1=5,
在Rt△PAM中,tan∠APB==;
(3)
过点P作PN⊥x轴,垂足为N,
∵S△PCD=S梯形PNOD﹣S△COD﹣S△PCN,
∴(1+a)×6﹣a2﹣(6﹣a)×1=3,
解得a1=1,a2=6,
答:a的值为1或6.
答案第1页,共2页
一、单选题
1.如图,在中,,则等于( )
A. B. C. D.
2.在下列网格中,小正方形的边长为1,点A,B,求∠A的余弦值( )
A. B. C. D.
3.如果∠A为锐角,cosA=,那么∠A 取值范围是( )
A.0°<∠A≤30° B.30°<∠A≤45° C.45°<∠A<60° D.60°<∠A<90°
4.如图,已知中,,,若,于点E,则( )
A. B. C. D.
5.如图,矩形ABCD中,AD=4,AB=5,E是AB边上的一点,连接DE、EC.若EC平分∠BED,则sin∠BCE的值是( )
A. B. C. D.
6.如图,菱形OABC的边OC在轴上,点A、B在第一象限内,,反比例函数的图象经过点A,若菱形的面积为4,则的值为( )
A.1 B.2 C.3 D.4
7.如图,在矩形ABCD中,AD=2,AB=1,以A为圆心,AD的长为半径画弧交BC于点E,则图中空白部分的面积是( )
A.1﹣ B.2﹣ C. D.2+
8.如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A. B. C. D.
9.如图,是的弦,,的延长线交于点,若,,则长为( )
A. B. C. D.
10.直角三角形纸片ABC的两条直角边BC,AC长分别为6,8,现将△ABC如图折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
11.如图,在矩形ABCD中,AB=2,AD=2,以AD的中点O为圆心的圆与边BC相切于点E,与边AB,CD分别交于点M,N,连结OM,ON,则的长为( )
A. B. C. D.
12.如图,A、B分别为反比例函数(x<0),y=(x>0)图象上的点,且OA⊥OB,则tan∠ABO的值为( )
A. B. C. D.
13.如图,正方形ABCD中,E、F分别为BC、CD边上的点,∠EAF=45°,则下列结论中正确的有( )
①BE+DF=EF;
②tan∠AMD=;
③BM2+DN2=MN2;
④若EF=1.5,△AEF的面积是3,则正方形ABCD的面积是4.
A.1个 B.2个 C.3个 D.4个
14.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE、AF,DE与AF交于点O.连接OC,则OC的值为( )
A. B.1 C. D.
15.如图,AB是半圆的直径,AC是一条弦,D是的中点,于点E,DE交AC于点F,DB交AC于点G,,则的值为( )
A. B. C. D.
二、填空题
16.计算:的结果为______.
17.若为锐角,已知,那么______°.
18.在矩形ABCD中,BC=2AB,点P在直线BC上,且PC=AB,则∠APB的正切值为_____.
19.已知,中,是锐角,,则的度数是__________.
20.小明沿着坡度为1∶的山坡走了100m,则他升高了______米.
三、解答题
21.计算:
(1)sin60° cos30°﹣1 (2)2sin30°+3cos60°﹣4tan45°
(3) (4)2tan60°+tan45°﹣4cos30°
22.先化简,再求值:
(1)÷(﹣a+2),其中a=2sin60°﹣3tan45°.
(2),其中x=2+tan30°.
23.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,且∠A,∠B都是锐角,求∠C的度数.
24.如图,点C是直径AB上一点.过C作交于点D,连接DA,DB.
(1)求证:;
(2)连接DO,过点D做的切线,交BA的延长线于点P.若,,求BC的长.
25.如图1,反比例函数y=的图象经过A(1,m)、B(2,1)两点,点P的坐标为(6,1).
(1)求反比例函数的表达式;
(2)连接PA、PB,求tan∠P的值;
(3)如图2,点C、D的坐标是(a,0)、(0,a)(0<a≤6),当△PCD的面积为3时,求a的值.
试卷第1页,共3页
参考答案:
1.B
解:解:由图可知, =
故答案选:B
2.C
解:点C如图所示:
AO==2,
cos∠A===,
故选:C.
3.C
解:∵cos60°=,cos45°=,且
∴45°<∠A<60°.
故选C.
4.D
解:连接AD,如图所示:
∵,BD=DC,
∴AD⊥BC,
∵,
∴,
∴,即,
∵,,
∴,
∴在Rt△ADB中,,
∴;
故选D.
5.A
解:四边形是矩形,,
,
,
平分,
,
,
,
,
,
,
,
故选:A.
6.B
解:过点A作AD⊥x轴于D,设菱形OABC的边长为x,
∵,
∴AD=OAsin∠AOC=,OD=OAcos∠AOC=,
∵菱形的面积为4,
∴OC·AD=,
∴k=xy=OD·AD=,
故选择B.
7.B
解:∵四边形ABCD是矩形,
∴∠B=90°,AD∥CB,
∵AB=1,AE=AD=2,
∴AE=2AB,
∴∠AEB=30°,
∴∠DAE=∠AEB=30°,
∴S阴==,
则图中空白部分的面积是
故选:B.
8.A
解:作于,
四边形是平行四边形,
.
.
是角平分线,
.
.
.
同理.
.
四边形是平行四边形.
,
四边形是菱形.
,,
,,,
,
,,
.
故选:A.
9.D
解:在中,,
::,
::,
,
,,
由勾股定理得,,
,
,
故选:D.
10.A
解:设CE=x,则AE=8﹣x,
∵△ABC如图折叠,使点A与点B重合,
∴BE=AE=8﹣x,
Rt△BCE中,CE2+BC2=BE2,
∴x2+62=(8﹣x)2,
解得x= ,
Rt△BCE中,
tan∠CBE=,
故选:A.
11.D
解:如图,连接OE,
∵⊙O与边BC相切于点E,
∴BC⊥OE,
∴∠OEB=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴四边形AOEB是矩形,
∵OE=AB=2,
∴OM=ON=OE=2,
∵AD=2,O为AD的中点,
∴OA=AD=×2=,
∴cos∠AOM==,
∴∠AOM=30°,
∵∠A=∠D=90°,OM=ON,OA=OD,
∴Rt△AOM≌Rt△DON(HL),
∴∠AOM=∠DON=30°,
∴∠MON=180°﹣30°﹣30°=120°,
∴l==π,
∴的长为π.
故选:D
12.A
解:如图,过A作AC⊥x轴于C,过B作BD⊥x轴于D
则∠BDO=∠ACO=90°
∵A、B分别为反比例函数(x<0),(x>0)图象上的点
∴S△AOC=4,S△BDO=9
∵∠AOB=90°
∴∠BOD+∠DBO=∠BOD+∠AOC=90°
∴∠DBO=∠AOC
∴△BDO∽△OCA
∴
∴
∴
故选:A.
13.C
解: ∵四边形ABCD为正方形,
∴AD=AB,∠ADF=90°,∠ABC=90°,
将△ADF顺时针旋转90°得到△ABF′,
∴AF=AF′,DF=BF′,∠DAF=∠BAF′,∠ADF=∠ADF′=90°,
∴∠F′BE=∠ABF′+∠ABE=90°+90°=180°,
∵∠BAE+∠DAF=90°-∠EAF=90°-45°=45°,
∴∠F′AE=∠FAB+∠BAE=∠DAF+∠BAE=45°=∠FAE,
在△AF′E和△AFE中,
,
∴△AF′E≌△AFE(SAS),
∴F′E=FE,
∴BE+DF=BE+BF′=F′E=EF,
故①正确;
∵BD为正方形的对角线,
∴∠ABM=∠FDN=45°=∠MAN,
∵∠ANM=∠DNF,
∴∠AMN=180°-∠MAN-∠ANM=180°-∠NDF-∠DNF=∠DFN,
∴tan∠AMN=tan∠DFA=,
故②正确;
将△AND顺时针旋转90°得到△ABN′,连结N′M,
∴AN=AN′,∠AND=∠ABN′=45°,DN=BN′,
∵∠N′AM=∠NAB+∠BAE=∠DAF+∠BAE=45°=∠NAM,
在△AN′M和△ANM中,
,
∴△AN′M≌△ANM(SAS),
∴N′M=NM,
∵∠N′BM=∠ABN′+∠ABM=45°+45°=90°,
∴根据勾股定理,即,
故③正确;
∵S△AEF=S△AF′E=3,F′E=FE=1.5,
∴,即,
∴AB=4,
∴S正方形ABCD=AB2=16,
故④不正确.
故选C.
14.B
解:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠DAE=90°,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAD=∠BAF+∠DAO=90°,
∴∠ADE+∠DAO=90°,
∴∠AOD=90°,
∵E、F分别为AB,BC的中点,
∴AE=AB,BF=BC,
∵AB=BC,
∴AE=BF,
过C作CG⊥DE于G,
∵∠OAD+∠ADO=∠ADO+∠CDG=90°,
∴∠OAD=∠CDG,
在△ADO和△DCG中,
,
∴△ADO≌△DCG(AAS),
∴AO=DG,
∵,
∴DO=2AO=2DG,
∴DG=OG,
∴CG为DO的垂直平分线,
∴OC=DC=1,
故选:B.
15.C
解:连接AD,BC,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠ADE+∠EDB=90°,
又∵DE⊥AB,
∴∠EDB+∠ABD=90°,
∴∠ADE=∠ABD,
∵D是的中点,
∴∠DAC=∠ABD,
∴∠ADE=∠DAC,
∴FA=FD;
∵∠ADE=∠DBC,∠ADE+∠EDB=90°,∠DBC+∠CGB=90°,
∴∠EDB=∠CGB,
又∵∠DGF=∠CGB,
∴∠EDB=∠DGF,
∴FD=FG,
∴FA=FD=FG,
∵在Rt△AEF中,,
∴设EF=3k,AE=4k,则AF=DF=FG=5k,AG=10k,DE=8k,
在Rt△ADE中,,
∵AB是直径,
∴∠ADG=∠GCB=90°,
∵∠AGD=∠CGB,
∴cos∠CGB=cos∠AGD,
∴,
在Rt△ADG中,,
∴,
故选:C.
16.
解:原式
,
故答案为:.
17.60
解:由为锐角,且,那么等于,
故填:60.
18.1或##或1
解:(1)如图①所示,
BC=2AB,PC=AB,
∴P是BC的中点,即BP=PC,
又∵四边形ABCD是矩形,
∴tan∠APB==1;
(2)如图②所示,
∵BC=2AB.PC=AB,
∴BP=3AB,
∴tan∠APB==.
综上所述∠APB的正切值为1或.
故答案为1或.
19.
解:∵中,是锐角,,
∴∠A=30°.
故答案为30°.
20.50
解:设升高了xm,根据坡比为1:,则可得水平距离为xm,
∴由勾股定理得x2+(x)2=1002,
解得x=50,x=-50(舍去),
故答案为50.
21.(1) (2) (3) (4)1
(1)
解:原式=
=
=;
(2)
原式=
=
=
(3)
解:
=
=
=
(4)
解:2tan60°+tan45°﹣4cos30°
=
=
=1
22.(1) (2);
(1)解:原式=
∵a=2sin60°-3tan45°
∴a=,
∴ 原式
(2)解:
原式
23.∠C=90°.
解:∵|sinA﹣|+(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,cosB=,
∴∠A=45°,∠B=45°,
∴∠C=180°﹣45°﹣45°=90°.
24.(1)见详解;
(2)240.
(1)
证明:∵为的直径
∴,
∵
∴
∴
(2)
解:∵为的切线
∴
∴
∵
∴
∵
∴
设,,则
∴,,
∴
∵
∴
∴
∴
25.(1)y=
(2)
(3)1或6
(1)
∵反比例函数y=的图象经过B(2,1)点,
∴k=2×1=2,
∴反比例函数的关系式为y=;
(2)
∵反比例函数y=的图象经过A(1,m)、
∴m=2,
∴A(1,2),
过点A作BP的垂线,交PB的延长线于点M,
则AM=2﹣1=1,MP=6﹣1=5,
在Rt△PAM中,tan∠APB==;
(3)
过点P作PN⊥x轴,垂足为N,
∵S△PCD=S梯形PNOD﹣S△COD﹣S△PCN,
∴(1+a)×6﹣a2﹣(6﹣a)×1=3,
解得a1=1,a2=6,
答:a的值为1或6.
答案第1页,共2页
