人教版八年级下册 18.2.1 矩形 课件(共22张)
文档属性
| 名称 | 人教版八年级下册 18.2.1 矩形 课件(共22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
18.2.1 矩形
第十八章 平行四边形
第1课时 矩形的性质
人教版八年级下册
18.2.特殊的平行四边形
温故知新
几何画板演示
新课学习
课堂小结
分层作业
温故知新
几何画板演示
新课学习
课堂小结
分层作业
平行四边形
边
角
对角线
对称性
平行四边形的对角相等、邻角互补
平行四边形的对边相等
平行四边形的对边平行
平行四边形的对角线互相平分
轴对称图形
1.理解矩形的概念,明确矩形与平行四边形的区别与联系;
2.探索并证明矩形的性质,会用矩形的性质解决简单的问题.
3.探索并掌握“直角三角形斜边上的中线等于斜边的一半”定理,会用它解决简单的问题。
18.2.1 矩形
第1课时 矩形的性质
学习目标
几何画板演示
课堂小结
分层作业
温故知新
新课学习
有一个角是直角的平行四边形是矩形。
矩形的定义:
平行四边形
矩形
有一个角
是直角
几何画板演示
课堂小结
分层作业
温故知新
新课学习
思考:
因为矩形是平行四边形,所以它具有平
行四边形的所有性质。
新课学习
课堂小结
分层作业
温故知新
几何画板
演示
A
D
B
C
O
由于它有一个角是直角,它是否具有一般平行四边形不具有的一些还有哪些特殊性质呢?
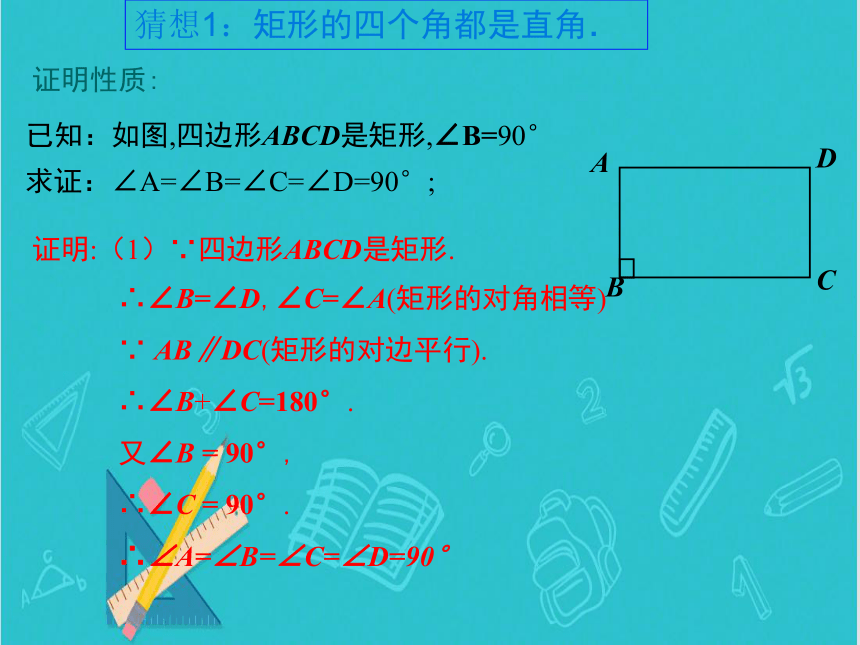
证明:(1)∵四边形ABCD是矩形.
∴∠B=∠D,∠C=∠A(矩形的对角相等)
∵ AB∥DC(矩形的对边平行).
∴∠B+∠C=180°.
又∠B = 90°,
∴∠C = 90°.
∴∠A=∠B=∠C=∠D=90°
证明性质:
已知:如图,四边形ABCD是矩形,∠B=90°
A
B
C
D
猜想1:矩形的四个角都是直角.
求证:∠A=∠B=∠C=∠D=90°;
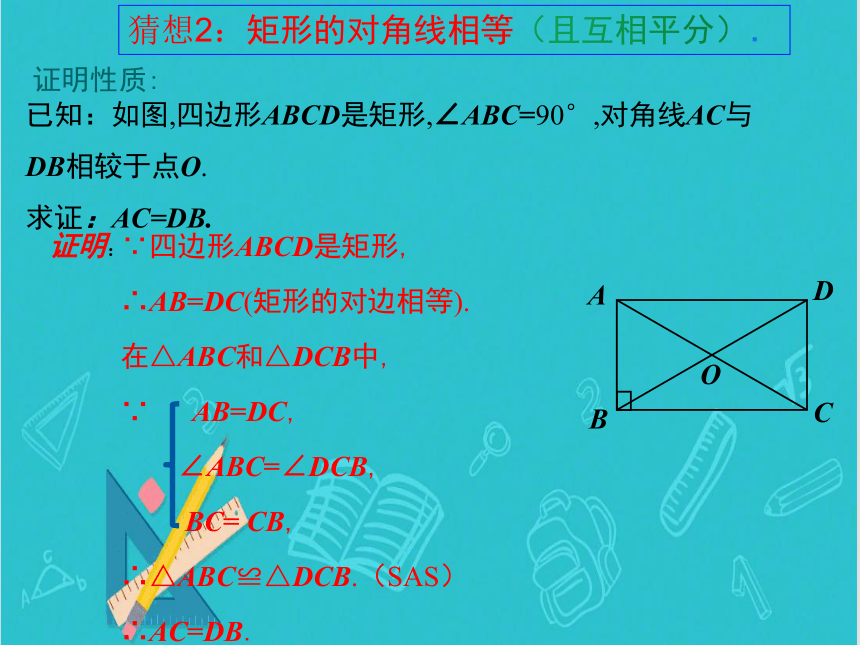
猜想2:矩形的对角线相等(且互相平分).
证明性质:
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.
求证:AC=DB.
∵四边形ABCD是矩形,
∴AB=DC(矩形的对边相等).
在△ABC和△DCB中,
∵ AB=DC,
∠ABC=∠DCB,
BC= CB,
∴△ABC≌△DCB.(SAS)
∴AC=DB.
A
B
C
D
O
证明:
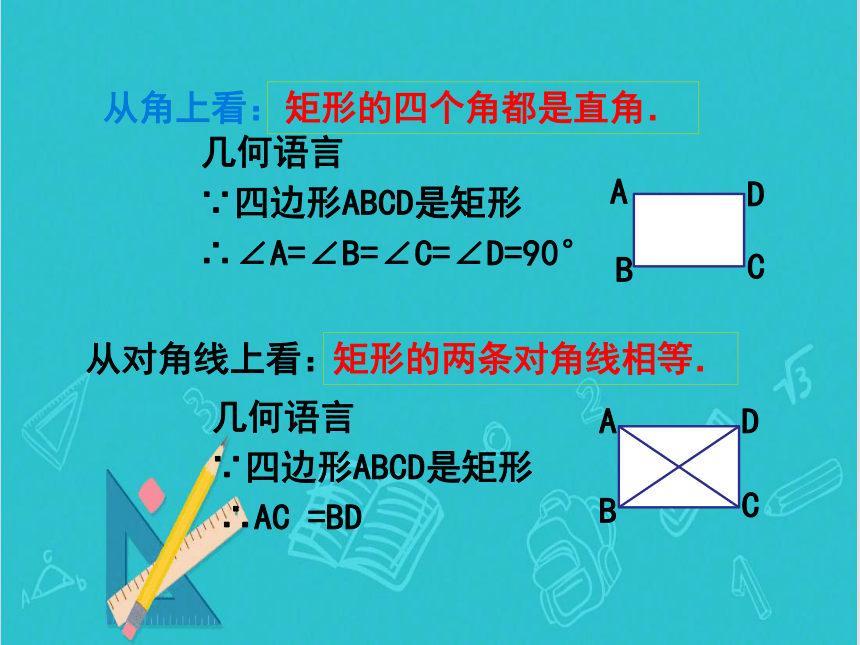
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
A
B
C
D
A
B
C
D
几何语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
几何语言
∵四边形ABCD是矩形
∴AC =BD
做一做:请同学们拿出准备好的矩形纸片,折一折,观察并思考.
矩形是不是轴对称图形 如果是,那么对称轴有几条
对称性: .
对称轴: .
轴对称图形
2条
学以致用(中考链接)
课堂小结
分层作业
温故知新
几何画板演示
新课学习
C
B
A
C
D
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
几何画板演示
课堂小结
分层作业
温故知新
新课学习
B
直角三角形斜边上中线
A
B
C
D
O
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?
它的长度与斜边AC有什么关系?
1
2
1
2
BO= BD= AC
猜想:直角三角形斜边上的中线等于斜边的一半.
几何画板演示
课堂小结
分层作业
温故知新
新课学习
O
C
B
A
D
证明: 延长BO至D, 使OD=BO,
连接AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴平行四边形ABCD是矩形
∴AC=BD
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO = AC
∴BO= BD= AC
1. 直角三角形斜边上的中线等于斜边的一半
性质
几何画板演示
课堂小结
分层作业
温故知新
新课学习
例1 如图,在矩形ABCD中,两条对角线相交于点O,
∠AOB=60°,AB=4 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形的对角线互相平分)
∴OA = OB.
∵∠AOB=60°,
∴ △ OAB是等边三角形
∴OA=AB=4
∴AC=BD = 2OA = 2 ×4 = 8.
A
B
C
D
O
当堂练习(模拟中考基础题)
课堂小结
分层作业
温故知新
几何画板演示
新课学习
1.(4分)(十堰中考)矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等
C.对角线相等 D.对角线互相平分
2.(4分)如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
C
D
3.(本溪中考)如图,BD是矩形ABCD的对角线,在BA和BD上分别截取BE,BF,使BE=BF;分别以E,F为圆心,以大于 EF的长为半径作弧,两弧在∠ABD内交于点G,作射线BG交AD于点P,若AP=3,则点P到BD的距离为 .
4.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
5.(上海中考)如图,已知直线l1∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上,如果边AB与l1的交点D是AB的中点,那么∠1= 度.
当堂练习(模拟中考基础题)
3
120
C
6.(8分)如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC的中点.求证:DM=MB.
当堂练习(模拟中考中档题)
7.(10分)如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.
求证:(1)△ABF≌△DEA;
(2)DF是∠EFC的平分线.
当堂练习(模拟中考拔高题)
边
角
对角线
平行
四边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
对边平行
且相等
四个角
都是直角
对角线互相
平分且相等
类比总结
矩形特有
的性质
说一说,这节课你有什么收获?
新课学习
分层作业
温故知新
几何画板演示
课堂小结
矩形是轴对称图形,连接对边中点的直线是它的两条对称轴.
直角三角形斜边上的中线等于斜边的一半.
分层作业
A:完成教材53页3个习题。
(每组5号、6号)
B:完成练习册本课时的习题。
(每组1、2、3、4号)
几何画板演示
新课学习
课堂小结
温故知新
课堂小结
谢 谢
18.2.1 矩形
第十八章 平行四边形
第1课时 矩形的性质
人教版八年级下册
18.2.特殊的平行四边形
温故知新
几何画板演示
新课学习
课堂小结
分层作业
温故知新
几何画板演示
新课学习
课堂小结
分层作业
平行四边形
边
角
对角线
对称性
平行四边形的对角相等、邻角互补
平行四边形的对边相等
平行四边形的对边平行
平行四边形的对角线互相平分
轴对称图形
1.理解矩形的概念,明确矩形与平行四边形的区别与联系;
2.探索并证明矩形的性质,会用矩形的性质解决简单的问题.
3.探索并掌握“直角三角形斜边上的中线等于斜边的一半”定理,会用它解决简单的问题。
18.2.1 矩形
第1课时 矩形的性质
学习目标
几何画板演示
课堂小结
分层作业
温故知新
新课学习
有一个角是直角的平行四边形是矩形。
矩形的定义:
平行四边形
矩形
有一个角
是直角
几何画板演示
课堂小结
分层作业
温故知新
新课学习
思考:
因为矩形是平行四边形,所以它具有平
行四边形的所有性质。
新课学习
课堂小结
分层作业
温故知新
几何画板
演示
A
D
B
C
O
由于它有一个角是直角,它是否具有一般平行四边形不具有的一些还有哪些特殊性质呢?
证明:(1)∵四边形ABCD是矩形.
∴∠B=∠D,∠C=∠A(矩形的对角相等)
∵ AB∥DC(矩形的对边平行).
∴∠B+∠C=180°.
又∠B = 90°,
∴∠C = 90°.
∴∠A=∠B=∠C=∠D=90°
证明性质:
已知:如图,四边形ABCD是矩形,∠B=90°
A
B
C
D
猜想1:矩形的四个角都是直角.
求证:∠A=∠B=∠C=∠D=90°;
猜想2:矩形的对角线相等(且互相平分).
证明性质:
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.
求证:AC=DB.
∵四边形ABCD是矩形,
∴AB=DC(矩形的对边相等).
在△ABC和△DCB中,
∵ AB=DC,
∠ABC=∠DCB,
BC= CB,
∴△ABC≌△DCB.(SAS)
∴AC=DB.
A
B
C
D
O
证明:
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
A
B
C
D
A
B
C
D
几何语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
几何语言
∵四边形ABCD是矩形
∴AC =BD
做一做:请同学们拿出准备好的矩形纸片,折一折,观察并思考.
矩形是不是轴对称图形 如果是,那么对称轴有几条
对称性: .
对称轴: .
轴对称图形
2条
学以致用(中考链接)
课堂小结
分层作业
温故知新
几何画板演示
新课学习
C
B
A
C
D
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
几何画板演示
课堂小结
分层作业
温故知新
新课学习
B
直角三角形斜边上中线
A
B
C
D
O
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?
它的长度与斜边AC有什么关系?
1
2
1
2
BO= BD= AC
猜想:直角三角形斜边上的中线等于斜边的一半.
几何画板演示
课堂小结
分层作业
温故知新
新课学习
O
C
B
A
D
证明: 延长BO至D, 使OD=BO,
连接AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴平行四边形ABCD是矩形
∴AC=BD
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO = AC
∴BO= BD= AC
1. 直角三角形斜边上的中线等于斜边的一半
性质
几何画板演示
课堂小结
分层作业
温故知新
新课学习
例1 如图,在矩形ABCD中,两条对角线相交于点O,
∠AOB=60°,AB=4 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形的对角线互相平分)
∴OA = OB.
∵∠AOB=60°,
∴ △ OAB是等边三角形
∴OA=AB=4
∴AC=BD = 2OA = 2 ×4 = 8.
A
B
C
D
O
当堂练习(模拟中考基础题)
课堂小结
分层作业
温故知新
几何画板演示
新课学习
1.(4分)(十堰中考)矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等
C.对角线相等 D.对角线互相平分
2.(4分)如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
C
D
3.(本溪中考)如图,BD是矩形ABCD的对角线,在BA和BD上分别截取BE,BF,使BE=BF;分别以E,F为圆心,以大于 EF的长为半径作弧,两弧在∠ABD内交于点G,作射线BG交AD于点P,若AP=3,则点P到BD的距离为 .
4.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
5.(上海中考)如图,已知直线l1∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上,如果边AB与l1的交点D是AB的中点,那么∠1= 度.
当堂练习(模拟中考基础题)
3
120
C
6.(8分)如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC的中点.求证:DM=MB.
当堂练习(模拟中考中档题)
7.(10分)如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.
求证:(1)△ABF≌△DEA;
(2)DF是∠EFC的平分线.
当堂练习(模拟中考拔高题)
边
角
对角线
平行
四边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
对边平行
且相等
四个角
都是直角
对角线互相
平分且相等
类比总结
矩形特有
的性质
说一说,这节课你有什么收获?
新课学习
分层作业
温故知新
几何画板演示
课堂小结
矩形是轴对称图形,连接对边中点的直线是它的两条对称轴.
直角三角形斜边上的中线等于斜边的一半.
分层作业
A:完成教材53页3个习题。
(每组5号、6号)
B:完成练习册本课时的习题。
(每组1、2、3、4号)
几何画板演示
新课学习
课堂小结
温故知新
课堂小结
谢 谢
