等腰三角形的性质2
图片预览




文档简介
课件17张PPT。等腰三角形的性质2等腰三角形的性质:
性质1 等腰三角形的两个底角相等(简写成“等边
对等角”).
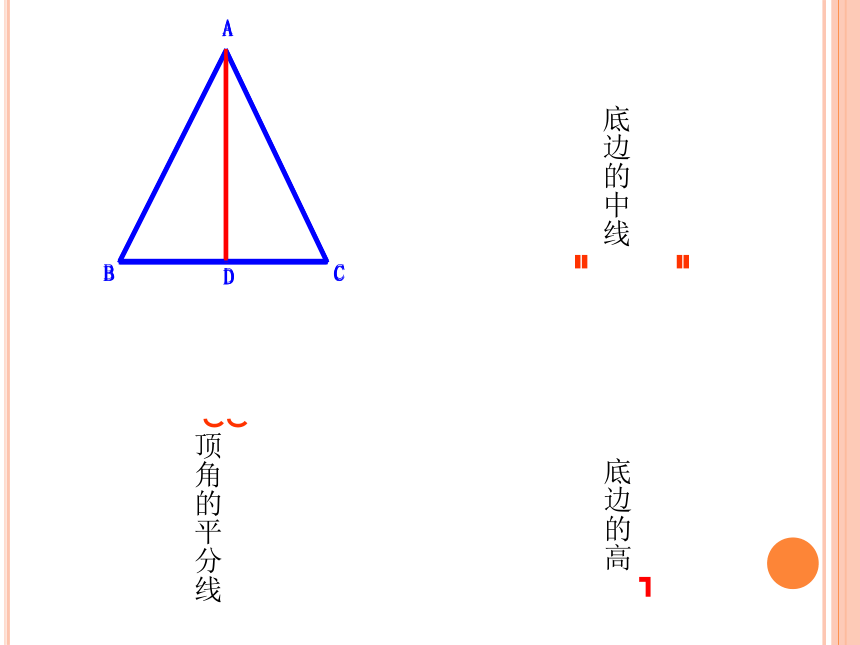
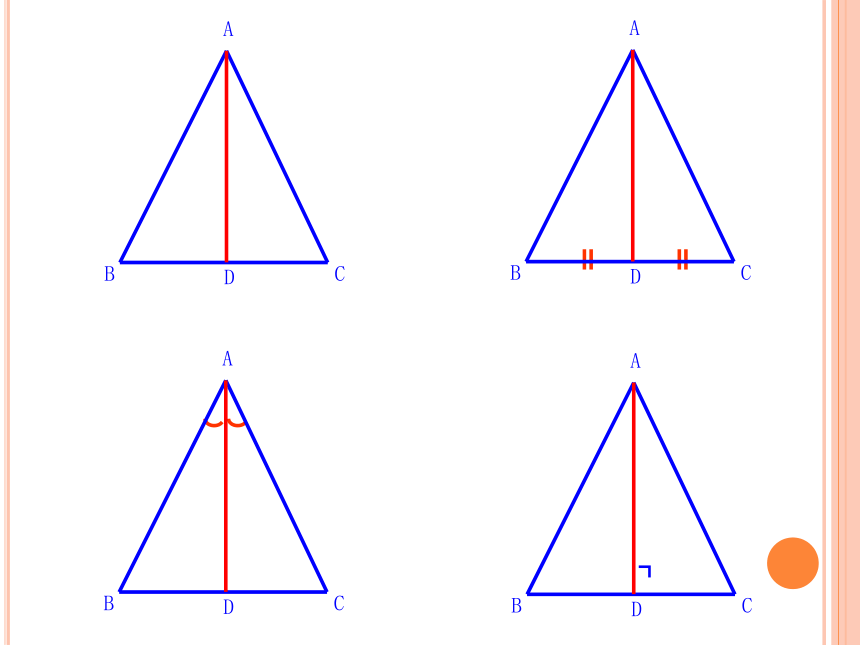
性质2 等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合( “三线合一”).
即:等腰三角形顶角的角平分线垂直平分底
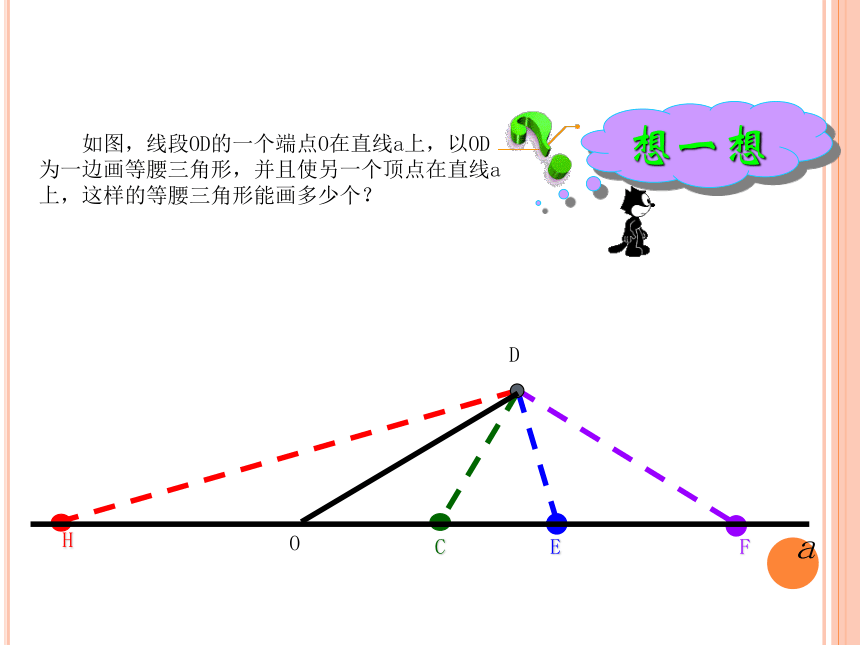
边.┓顶角的平分线底边的高底边的中线 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?CEFH① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°在等腰三角形中,⑤0°<底角<90° 例2 如图,在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,求△ABC各角的度数. 解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角).
设∠A=x,则∠BDC = ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x. 于是在△ABC中,有∠A+∠ABC+∠C =x+2x+2x=180°,
解得 x=36°,
在△ABC中,∠A==36°,∠ABC=∠C=72°.例3 求证:斜边和一条直角边对应相等的两个直角三角形全等。
已知:如图,在Rt△ABC和Rt △A’B’C’中, ∠C= ∠C’=90 ° AB=A’B’,AC=A’C’
求证:Rt△ABC ≌ Rt △A’B’C
ABCCA’B’C’AA’CC’BB’证明:移动Rt△ABC和Rt △A’B’C’,使点A与点A’,点C与点C’重合,点B与点B’在AC的两侧
∵ ∠BCB’=90 °+90 °=180 °(等式性质)
∴B,C,B’三点在一条直线上(平角的定义)
在ABB’中,
∵AB=AB’(已知)
∴ ∠ B=∠B’(等边对等角)
在Rt△ABC和Rt △A’B’C’中,
∠ACB= ∠ A’C’B’(已知)
∠ B=∠ B’(已证)
AB=A’B’(已知)
∴Rt△ABC≌Rt △A’B’C’(AAS) 等腰三角形的一个内角是另一个内角的2倍,则三个内角分别为_________________. 解:设小角为x,则大角为2x.
当x为底角时,x +x+ 2x=180°,
解得 x=45°,则2x=90°.
当x为顶角时, x +2x+ 2x=180°,
解得x =36° ,则2x=72°. ∴其内角的度数为45°,45°,90°,或36°,72°,72°.有两条边相等的三角形叫做等腰三角形.二、性质1.等边对等角. 2. “三线合一”:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.一、定义1.(1)如果等腰三角形的一个底角为50°,则其
余两个角为____和____.(2)如果等腰三角形的顶角为80°,则它的一个底角为____.50°80°50°(3)如果等腰三角形的一个角为80°,则其余两个角为________________________.80°和20°(4)如果等腰三角形的一个角为100°,则其余两个角为_________.40°和40°或50°和50 °2.如图,∠A=15°,AB=BC=CD=DE=EF,则
∠DEF等于( )
A.90° B.75°
C.70° D.60°D3.(黄冈中考题)在△ABC中, AB=AC,AB的
中垂线与AC所在的直线相交得的锐角为50°,
则底角的大小为___________.70°或 20°4.已知AD = DC=CB,∠A= 25°,则∠DCB
的度数为________.80°课堂作业:129页练习2,4题。
性质1 等腰三角形的两个底角相等(简写成“等边
对等角”).
性质2 等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合( “三线合一”).
即:等腰三角形顶角的角平分线垂直平分底
边.┓顶角的平分线底边的高底边的中线 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?CEFH① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°在等腰三角形中,⑤0°<底角<90° 例2 如图,在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,求△ABC各角的度数. 解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角).
设∠A=x,则∠BDC = ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x. 于是在△ABC中,有∠A+∠ABC+∠C =x+2x+2x=180°,
解得 x=36°,
在△ABC中,∠A==36°,∠ABC=∠C=72°.例3 求证:斜边和一条直角边对应相等的两个直角三角形全等。
已知:如图,在Rt△ABC和Rt △A’B’C’中, ∠C= ∠C’=90 ° AB=A’B’,AC=A’C’
求证:Rt△ABC ≌ Rt △A’B’C
ABCCA’B’C’AA’CC’BB’证明:移动Rt△ABC和Rt △A’B’C’,使点A与点A’,点C与点C’重合,点B与点B’在AC的两侧
∵ ∠BCB’=90 °+90 °=180 °(等式性质)
∴B,C,B’三点在一条直线上(平角的定义)
在ABB’中,
∵AB=AB’(已知)
∴ ∠ B=∠B’(等边对等角)
在Rt△ABC和Rt △A’B’C’中,
∠ACB= ∠ A’C’B’(已知)
∠ B=∠ B’(已证)
AB=A’B’(已知)
∴Rt△ABC≌Rt △A’B’C’(AAS) 等腰三角形的一个内角是另一个内角的2倍,则三个内角分别为_________________. 解:设小角为x,则大角为2x.
当x为底角时,x +x+ 2x=180°,
解得 x=45°,则2x=90°.
当x为顶角时, x +2x+ 2x=180°,
解得x =36° ,则2x=72°. ∴其内角的度数为45°,45°,90°,或36°,72°,72°.有两条边相等的三角形叫做等腰三角形.二、性质1.等边对等角. 2. “三线合一”:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.一、定义1.(1)如果等腰三角形的一个底角为50°,则其
余两个角为____和____.(2)如果等腰三角形的顶角为80°,则它的一个底角为____.50°80°50°(3)如果等腰三角形的一个角为80°,则其余两个角为________________________.80°和20°(4)如果等腰三角形的一个角为100°,则其余两个角为_________.40°和40°或50°和50 °2.如图,∠A=15°,AB=BC=CD=DE=EF,则
∠DEF等于( )
A.90° B.75°
C.70° D.60°D3.(黄冈中考题)在△ABC中, AB=AC,AB的
中垂线与AC所在的直线相交得的锐角为50°,
则底角的大小为___________.70°或 20°4.已知AD = DC=CB,∠A= 25°,则∠DCB
的度数为________.80°课堂作业:129页练习2,4题。
