求二次函数解析式
图片预览




文档简介
课件13张PPT。求二次函数解析式根据图象信息,写出这个二次函数解析式。y=2x2y=x2-2xy = x2 - 2x -3
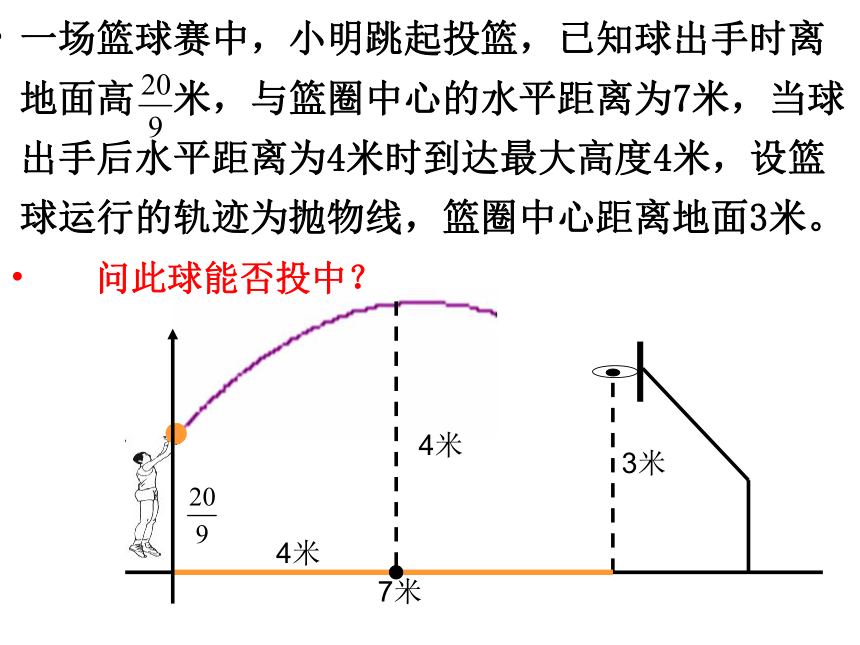
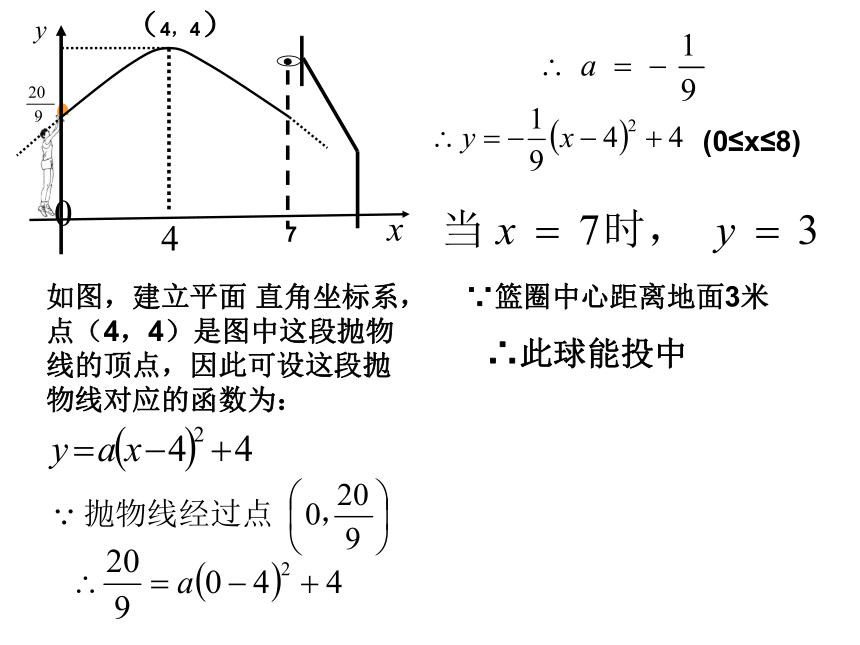
y=(x-1)2-1y=(x-1)2-4已知抛物线与X轴交于A(-1, 0),B(2,0)并经过点M(0,1),求抛物线的解析式? 已知一个二次函数的图象过点(-1,10)、(1,4)、(2,7)三点,求这个函数的解析式?一般式: y=ax2+bx+c两根式:y=a(x-x1)(x-x2)来到操场一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。 问此球能否投中?3米7米4米4米如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:(0≤x≤8)∵篮圈中心距离地面3米∴此球能投中如图所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线AB为x轴,AB的中点为原点建立坐标系.
①求此桥拱线所在抛物线的解析式.
②桥边有一浮在水面部分高4m,最宽处12m的观光船,试探索此船能否开到桥下?说明理由.来到永州如图所示,已知抛物线y=ax2+bx+c与x轴负半轴交于A、B两点,与y轴交于点C,且OB= ,CB=2 ,∠CAO=30°,求抛物线的解析式和它的顶点坐标. OA= 3OC= 3回到课堂1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。 y=-2x2+4x直面中考
2、已知一条抛物线与抛物线y=-x2-3x+7的形状相同,
顶点在直线x=1上,且顶点到x轴的距离为5,请写出
满足此条件的抛物线的解析式.其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
3、某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水呈抛物线状(抛物线所在平面与墙面垂直,如图所示).如果抛物线的最高点M离墙1米,离地面40/3米,则水流落地点B离墙的距离OB是 ( )
A.2米 B.3米 C.4米 D.5米BO①抛物线顶点M(1,40/3)
与y轴交点A(0,10) ②求得抛物线解析式;③求出抛物线与x轴的交点;提示(-1,0) (3,0)140/310Y=- x2 + x+10 4、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。5、如图所示,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4,x1x2=3,
(1)求此抛物线的解析式;
(2)设此抛物线与y轴的交点为C,过点B、C作直线,求此直线的解析式;
(3)求△ABC的面积.
(1)y= -x2+4x-3 (2) y= x-3 (3) 3
y=(x-1)2-1y=(x-1)2-4已知抛物线与X轴交于A(-1, 0),B(2,0)并经过点M(0,1),求抛物线的解析式? 已知一个二次函数的图象过点(-1,10)、(1,4)、(2,7)三点,求这个函数的解析式?一般式: y=ax2+bx+c两根式:y=a(x-x1)(x-x2)来到操场一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。 问此球能否投中?3米7米4米4米如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:(0≤x≤8)∵篮圈中心距离地面3米∴此球能投中如图所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线AB为x轴,AB的中点为原点建立坐标系.
①求此桥拱线所在抛物线的解析式.
②桥边有一浮在水面部分高4m,最宽处12m的观光船,试探索此船能否开到桥下?说明理由.来到永州如图所示,已知抛物线y=ax2+bx+c与x轴负半轴交于A、B两点,与y轴交于点C,且OB= ,CB=2 ,∠CAO=30°,求抛物线的解析式和它的顶点坐标. OA= 3OC= 3回到课堂1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。 y=-2x2+4x直面中考
2、已知一条抛物线与抛物线y=-x2-3x+7的形状相同,
顶点在直线x=1上,且顶点到x轴的距离为5,请写出
满足此条件的抛物线的解析式.其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
3、某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水呈抛物线状(抛物线所在平面与墙面垂直,如图所示).如果抛物线的最高点M离墙1米,离地面40/3米,则水流落地点B离墙的距离OB是 ( )
A.2米 B.3米 C.4米 D.5米BO①抛物线顶点M(1,40/3)
与y轴交点A(0,10) ②求得抛物线解析式;③求出抛物线与x轴的交点;提示(-1,0) (3,0)140/310Y=- x2 + x+10 4、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。5、如图所示,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4,x1x2=3,
(1)求此抛物线的解析式;
(2)设此抛物线与y轴的交点为C,过点B、C作直线,求此直线的解析式;
(3)求△ABC的面积.
(1)y= -x2+4x-3 (2) y= x-3 (3) 3
