人教A版2019必修第一册4.4.1对数函数的概念课件(32张PPT)
文档属性
| 名称 | 人教A版2019必修第一册4.4.1对数函数的概念课件(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 827.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 17:55:52 | ||
图片预览







文档简介
第四章 指数函数与对数函数
人教A版2019 必修第一册
4.4 对数函数
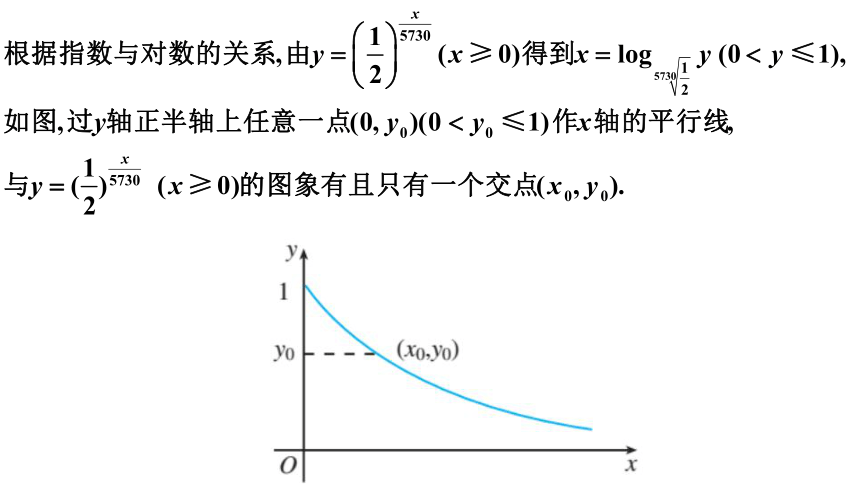
思考:在4.2.1的问题2中,我们已经研究了死亡生物体内碳14的含量y随死亡时间x的变化而衰减的规律.反过来,已知死亡生物体内碳14的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间x是碳14的含量y的函数吗?
例2 假设某地初始物价为1,每年以5%的增长率递增,经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
所以,该地区的物价大约经过14年后会翻一番.
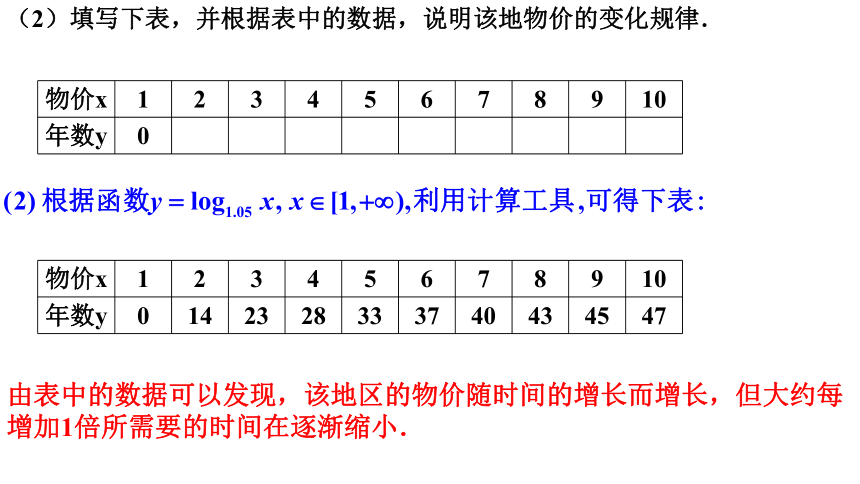
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价x
1
2
3
4
5
6
7
8
9
10
年数y
0
物价x
1
2
3
4
5
6
7
8
9
10
年数y
0
14
23
28
33
37
40
43
45
47
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增加1倍所需要的时间在逐渐缩小.
X
1/4
1/2
1
2
4
……
y=log2x
-2
-1
0
1
2
……
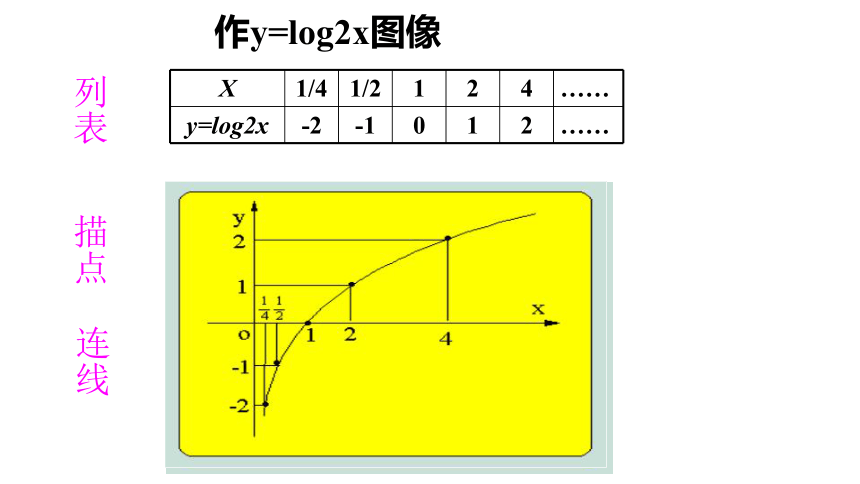
列表
描点
作y=log2x图像
连线
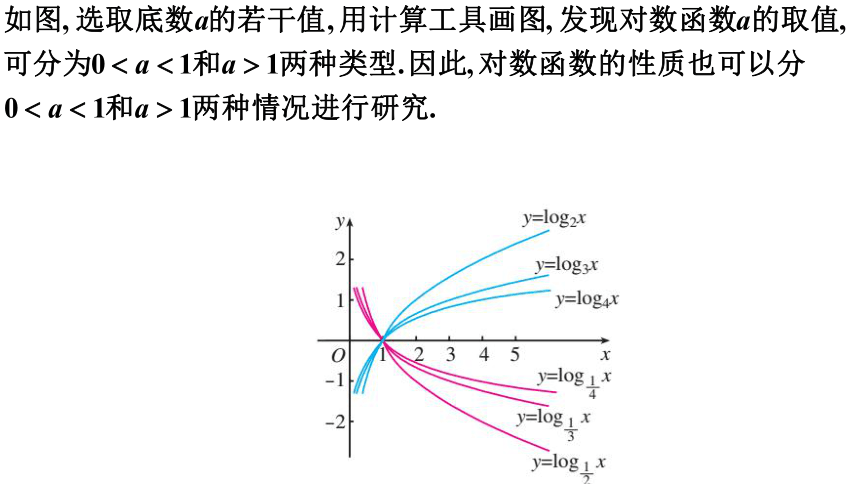
0 a>1
图象
定义域
值域
性质
(2)减函数
(2)增函数
练一练:
x
y
0
1
y=log a x
y=log b x
y=log c x
y=log d x
比较a、b、c、d、1的大小。
答:b>a>1>d>c
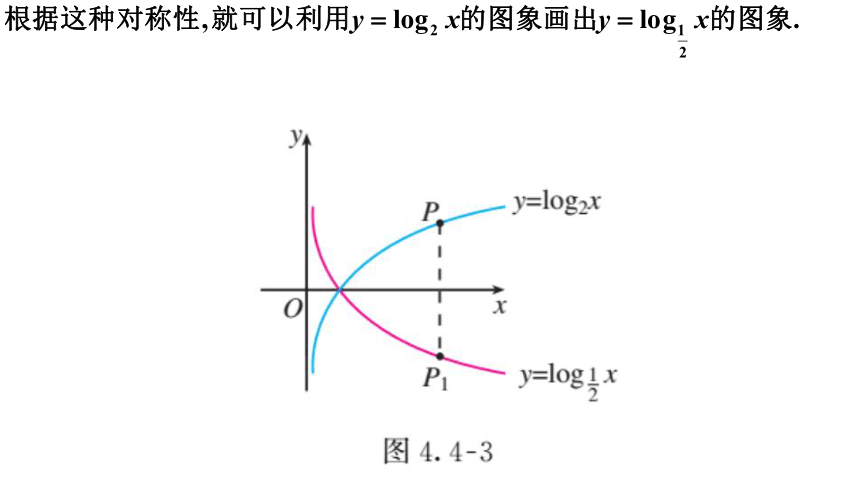
同底数的指数函数和对数函数互为反函数.
在前面的学习中我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
x
y=2x
y=2x
0
1
0
0.5
1.414
1
1
2
2
1.5
2.828
3
2
4
4
2.5
5.657
5
3
8
6
x
y=2x
y=2x
0
1
0
2
4
4
4
16
8
6
64
12
8
256
16
10
1 024
20
12
4 096
24
指数函数不像一次函数那样按同一速度增长,而是越来越快,呈爆炸性增长.
利用信息技术,列出上述两个函数的自变量与函数值的对应值表(表4.4-5),并在同一直角坐标系中画出它们的图象(图4.4-7).
表4.4-5
x
y=lgx
y=x/10
0
不存在
0
10
1
1
20
1.301
2
30
1.477
3
40
1.602
4
50
1.699
5
60
1.778
6
…
…
…
对数函数比较适合于描述增长速度平缓的变化规律
(3)讨论交流“直线上升”“ 对数增长”“ 指数爆炸”的含义.
人教A版2019 必修第一册
4.4 对数函数
思考:在4.2.1的问题2中,我们已经研究了死亡生物体内碳14的含量y随死亡时间x的变化而衰减的规律.反过来,已知死亡生物体内碳14的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间x是碳14的含量y的函数吗?
例2 假设某地初始物价为1,每年以5%的增长率递增,经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
所以,该地区的物价大约经过14年后会翻一番.
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价x
1
2
3
4
5
6
7
8
9
10
年数y
0
物价x
1
2
3
4
5
6
7
8
9
10
年数y
0
14
23
28
33
37
40
43
45
47
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增加1倍所需要的时间在逐渐缩小.
X
1/4
1/2
1
2
4
……
y=log2x
-2
-1
0
1
2
……
列表
描点
作y=log2x图像
连线
0
图象
定义域
值域
性质
(2)减函数
(2)增函数
练一练:
x
y
0
1
y=log a x
y=log b x
y=log c x
y=log d x
比较a、b、c、d、1的大小。
答:b>a>1>d>c
同底数的指数函数和对数函数互为反函数.
在前面的学习中我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
x
y=2x
y=2x
0
1
0
0.5
1.414
1
1
2
2
1.5
2.828
3
2
4
4
2.5
5.657
5
3
8
6
x
y=2x
y=2x
0
1
0
2
4
4
4
16
8
6
64
12
8
256
16
10
1 024
20
12
4 096
24
指数函数不像一次函数那样按同一速度增长,而是越来越快,呈爆炸性增长.
利用信息技术,列出上述两个函数的自变量与函数值的对应值表(表4.4-5),并在同一直角坐标系中画出它们的图象(图4.4-7).
表4.4-5
x
y=lgx
y=x/10
0
不存在
0
10
1
1
20
1.301
2
30
1.477
3
40
1.602
4
50
1.699
5
60
1.778
6
…
…
…
对数函数比较适合于描述增长速度平缓的变化规律
(3)讨论交流“直线上升”“ 对数增长”“ 指数爆炸”的含义.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
