2021-2022学年北师大版数学九年级下册2.2二次函数的图像与性质课后培优(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册2.2二次函数的图像与性质课后培优(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 20:22:10 | ||
图片预览



文档简介
二次函数的图像与性质
一、单选题
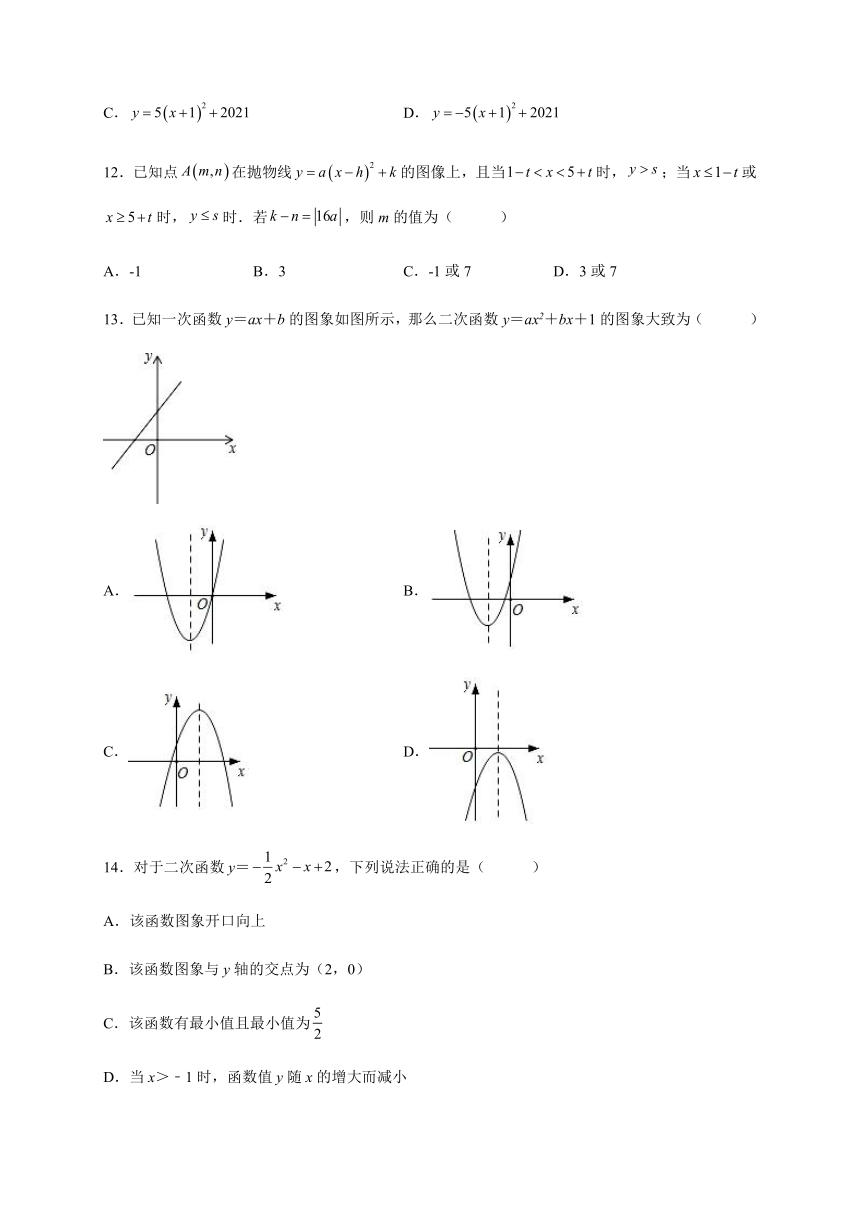
1.函数是二次函数,函数有最大值,则a满足( )
A. B. C. D.a为任意实数
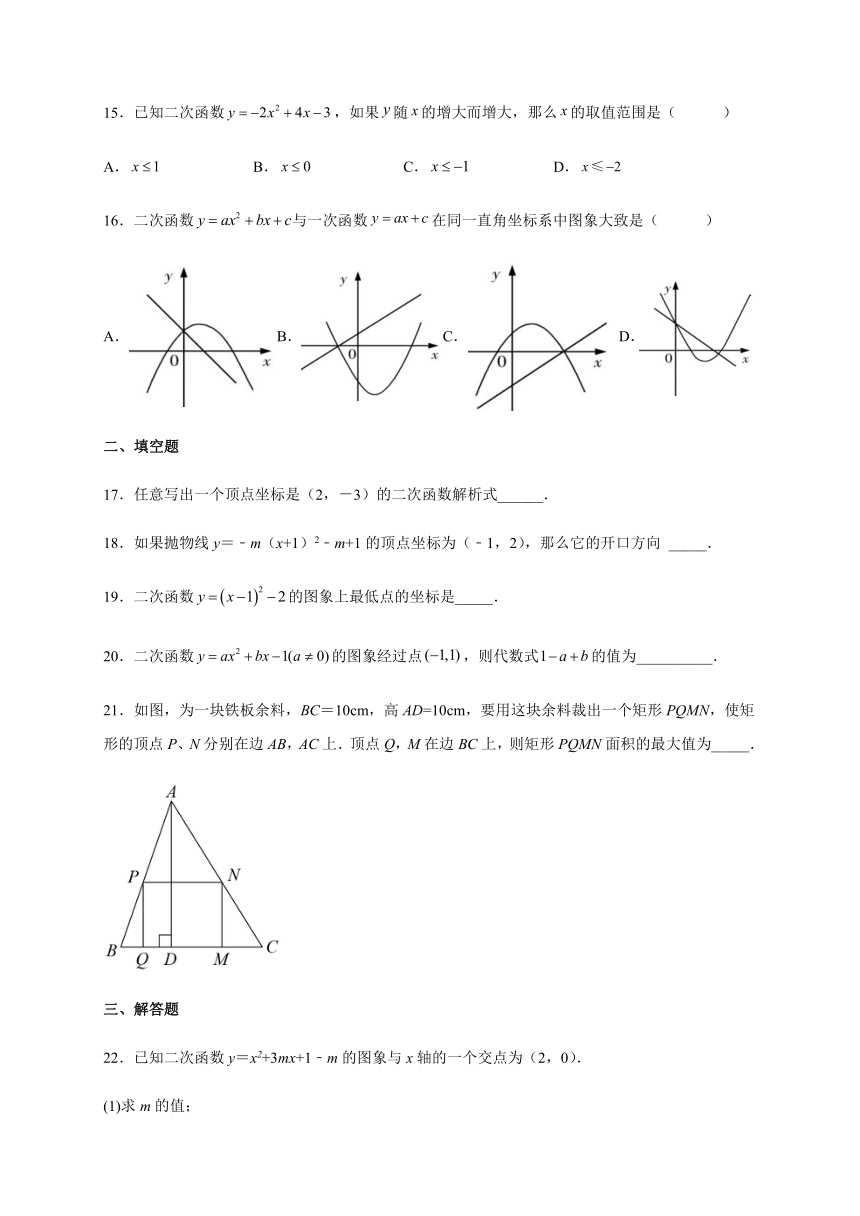
2.已知点(1,y1),(2,y2)都在函数y=﹣x2的图象上,则( )
A.y1<y2 B.y1>y2
C.y1=y2 D.y1,y2大小不确定
3.抛物线y=(x+3)2+2的对称轴是( )
A.直线x=3 B.直线x=-3 C.直线x=2 D.直线x=-2
4.抛物线的顶点坐标是( )
A. B. C. D.
5.抛物线y=ax2+bx+c(a<0)与x轴的一个交点坐标为(﹣2,0),对称轴为直线x=2,当y>0时,x的取值范围是( )
A.x>﹣2 B.x<6 C.﹣2<x<6 D.x<﹣2或x>6
6.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B的坐标为(1,0),下面的四个结论:① abc>0;② a-b+c<0;③ 2a-b=0;④3a+c>0.其中正确结论个数有( ).
A.1个 B.2个 C.3个 D.4个
7.抛物线沿x 轴向右平移2个单位后的顶点坐标是( ).
A.(0,2) B.(0,-2) C.(2,0) D.(-2,0)
8.抛物线向左平移2个单位,再向上平移5个单位,所得抛物线解析式为( )
A. B.
C. D.
9.对于二次函数y= 3(x 1)2+5,下列说法正确的是( )
A.函数图象的开口向上 B.函数图象的对称轴为直线
C.函数的最小值为5 D.当时,y随x的增大而增大
10.已知点在二次函数的图象上,且C为抛物线的顶点.若,则m的取值范围是( )
A. B. C. D.
11.已知一抛物线与二次函数图象的开口大小相同,开口方向相同且顶点坐标为(-1,2021),则该抛物线对应的函数表达式为( )
A. B.
C. D.
12.已知点在抛物线的图像上,且当时,;当或时,时.若,则m的值为( )
A.-1 B.3 C.-1或7 D.3或7
13.已知一次函数y=ax+b的图象如图所示,那么二次函数y=ax2+bx+1的图象大致为( )
A. B.
C. D.
14.对于二次函数y=,下列说法正确的是( )
A.该函数图象开口向上
B.该函数图象与y轴的交点为(2,0)
C.该函数有最小值且最小值为
D.当x>﹣1时,函数值y随x的增大而减小
15.已知二次函数,如果随的增大而增大,那么的取值范围是( )
A. B. C. D.
16.二次函数与一次函数在同一直角坐标系中图象大致是( )
A.B.C. D.
二、填空题
17.任意写出一个顶点坐标是(2,-3)的二次函数解析式______.
18.如果抛物线y=﹣m(x+1)2﹣m+1的顶点坐标为(﹣1,2),那么它的开口方向 _____.
19.二次函数的图象上最低点的坐标是_____.
20.二次函数的图象经过点,则代数式的值为__________.
21.如图,为一块铁板余料,BC=10cm,高AD=10cm,要用这块余料裁出一个矩形PQMN,使矩形的顶点P、N分别在边AB,AC上.顶点Q,M在边BC上,则矩形PQMN面积的最大值为_____.
三、解答题
22.已知二次函数y=x2+3mx+1﹣m的图象与x轴的一个交点为(2,0).
(1)求m的值;
(2)求这个函数图象与x轴另一个交点的横坐标.
23.如图,直线与抛物线交于,两点,与轴于点,其中点的坐标为.
(1)求,的值;
(2)若于点,.试说明点在抛物线上.
24.设二次函数y=(mx﹣2)(x﹣2m),其中m是常数.
(1)当m=2时,试判断点(1,0)是否在该函数图象上;
(2)用含m的代数式表示函数的对称轴;
(3)当x≥﹣2时,y随x的增大而减小,求m的范围
25.如图,二次函数的图象交x轴于A,B两点,交y轴于点C,点D是BC上方抛物线上的一点,过D作AC的平行线,交BC于点E.
(1)求△ABC的面积;
(2)连接CD,当CD∥x轴时,求△CDE的面积;
(3)求DE的最大值.
26.如图,在ABC中,∠B=90°,AB=6mm,BC=12mm,动点P从点A开始沿边AB向点B以1mm/s的速度移动,动点Q从点B开始沿边BC向点C以2mm/s的速度移动,且与点P同时出发.设PBQ的面积为S,动点移动的时间为t(t>0).
(1)当t=4时,求S的值;
(2)求S关于t的函数解析式;
(3)t为何值时,S的值最大?
试卷第1页,共3页
参考答案:
1.A
解:当抛物线开口向下,在顶点处产生最大值,
故,
故A符合题意,B、C、D不符合题意,
故选:A.
2.B
解:∵点(1,y1),(2,y2)都在函数y=﹣x2的图象上,
∴,,
∴,
故选B.
3.B
解:抛物线y=(x+3)2+2的顶点坐标为(-3,2),
故该抛物线的对称轴是直线x=-3.
故选:B.
4.A
解:∵,
∴此函数的顶点坐标为(3,1),
故选:A.
5.C
解:∵抛物线对称轴为直线x=2,与x轴一个交点坐标为(-2,0),
∴抛物线与x轴另一交点坐标为(6,0),
∴当y>0时,x的取值范围是﹣2故选:C.
6.B
解:,
∴,
∵抛物线开口向上,a>0,
∴>0,
抛物线y=ax2+bx+c(a≠0)的图象与y轴交点在y轴负半轴,
∴c<0,
∴abc<0,
故①不正确;
当x=﹣1时,y=a﹣b+c函数值为负数,
∴a﹣b+c<0,
故②正确;
∵,
∴,
故③正确;
∵点B的坐标为(1,0),
∴,
∵,
∴,
故④不正确;
综上②③正确,只有两个,
故选:B
7.C
解:∵抛物线的顶点坐标为(0,0),
则平移后抛物线为,顶点坐标为(2,0)
∴向右平移2个单位后的顶点坐标是(2,0).
故选C.
8.D
解:∵抛物线向左平移2个单位,再向上平移5个单位,
∴所得抛物线解析式为
故选D
9.D
解:二次函数y=-3(x-1)2+5
∵-3<0,
∴二次函数的的图象的开口向下,对称轴为直线x=1,最大值为5,
当x<1时,y随x的增大而增大,
故选:D.
10.B
解:抛物线的对称轴为直线
点C为抛物线的顶点
点C为抛物线的最低点,即抛物线开口向上
点
,
故选:B.
11.D
解:∵抛物线与二次函数图象的开口大小相同,开口方向相同且顶点坐标为(-1,2021),
∴该抛物线对应的函数表达式为.
故选:D
12.C
解:由题意可得抛物线对称轴为直线,且开口向下,
,,
,
点在抛物线上,
,
,
,
解得或,
故选:C.
13.B
解:∵y=ax+b的图象经过一、二、三象限,
∴a>0,b>0,
∴﹣<0,
∴二次函数y=ax2+bx+1的图象开口向上,对称轴在y轴的左侧,交y轴的正半轴.
故选:B
14.D
解:∵
∴
∴该函数图象开口向下
故A选项错误;
∵当x=0时,y=2,
∴函数图象与y轴的交点为(0,2)
故B选项错误;
∵,
∴该函数有最大值且最大值为
故C选项错误;
∵该抛物线的对称轴为:直线,图象开口向下
∴当x>﹣1时,函数值y随x的增大而减小.
故D选项正确.
故选:D.
15.A
解:
抛物线开口方向向下,对称轴为直线
当时,随的增大而增大.
故选:A.
16.A
解:A.图象中二次函数,一次函数,故A符合题意.
B.图象中二次函数,一次函数,故B不符合题意.
C.图象中二次函数,一次函数,故C不符合题意.
D.图象中二次函数,一次函数,故D不符合题意.
故选:A.
17.(答案不唯一)
解:满足顶点坐标是的二次函数解析式为,
故答案为:(答案不唯一).
18.向上
解:∵抛物线的顶点坐标为(-1,2),
∴,
∴,
∴抛物线解析式为,
∴抛物线的开口向上,
故答案为:向上.
19.
解:对于二次函数,
当时,随的增大而减小;当时,随的增大而增大,
所以此二次函数的顶点即为图象上的最低点,
因为二次函数的顶点坐标为,
所以此函数图象上最低点的坐标是,
故答案为:.
20.﹣1
解:∵二次函数y=ax2+bx﹣1(a≠0)的图象经过点(﹣1,1),
∴a﹣b﹣1=1,
∴1﹣a+b
=﹣(a﹣b﹣1)
=﹣1.
故答案为:﹣1
21.25
解:设DE=x,
∵四边形PQMN是矩形,AD⊥BC,
∴,PQ=MN=DE,
∴△APN∽△ABC,
∴,
∴,
∴PN=10-x,
∴矩形PQMN面积=,
∴当x=5时,矩形PQMN面积有最大值,最大值为25cm2,
故答案为:25.
.
22.(1);
(2)函数图象与x轴另一个交点的横坐标为1
(1)
∵二次函数y=x2+3mx+1﹣m的图象与x轴的一个交点为(2,0),
∴4+6m+1﹣m=0,
解得:m=﹣1;
(2)
由(1)得:二次函数解析式为y=x2﹣3x+2,
令y=0,则x2﹣3x+2=0,
解得:x1=1,x2=2,
∴函数图象与x轴另一个交点的横坐标为1.
23.(1),
(2)见解析
(1)
把点A(-4,8)代入,得:
∴;
把点A(-4,8)代入,得:
∴;
(2)
如图,分别过点A,D作AM⊥y轴于点M,DN⊥y轴于点N.
∵直线AB的解析式为y=-x+6,
令x=0,则y=6
∴C(0,6),
∵∠AMC=∠DNC=∠ACD=90°,
∴∠ACM+∠DCN=90°,∠DCN+∠CDN=90°,
∴∠ACM=∠CDN,
∵CA=CD,
∴△AMC≌△CND(SAS),
∴CN=AM=4,DN=CM=2,
∴D(-2,2),
当x=-2时,y=×22=2,
∴点D在抛物线y=x2上.
24.(1)(1,0)在该函数图象上
(2)x
(3)m≤﹣2
(1)
解:当m=2时,y=(2x﹣2)(x﹣4),
取x=1,则y=(2﹣2)×(1﹣2)=0,
∴(1,0)在该函数图象上;
(2)
∵y=(mx﹣2)(x﹣2m),
∴函数图象与x轴的交点为,,
∴抛物线的对称轴为x=;
(3)
∵当x≥﹣2时,y随x的增大而减小,
∴,
解得m≤﹣2,
∴m的范围为m≤﹣2.
25.(1);
(2);
(3)
(1)
解:当x=0时,y=3,
∴C(0,3),OC=3,
当y=0时,﹣x2+x+3=0,
解得:x=﹣3或x=6,
∴A(﹣3,0),B(6,0),
∴AB=9,
∴S△ABC=.
(2)
解:∵C(0,3),CD∥x轴,
∴D(3,3),∠DCE=∠ABC,
∴CD=3,
∵DE∥AC,
∴∠DEC=∠ACB,
∴△DEC∽△ACB,
∴,
∵S△ABC=,
∴S△DEC=.
(3)
解:如图,过点D作DF∥y轴交BC于点F,过点E作EH⊥DF于点H,
∵DE∥AC,DF∥y轴,
∴∠DEF的度数不变,∠EFD的度数不变,
∴在点D的移动过程中△DEF的形状保持不变,
∴当DF最大时,DE的长度也最大,
设直线BC的解析式为y=kx+b,
则,解得:,
∴直线BC的解析式为y=﹣x+3,
设点D的坐标(x,﹣x2+x+3),则点F的坐标(x,﹣x+3),
∴DF=﹣x2+x+3﹣(﹣x+3)=﹣x2+x=﹣(x﹣3)2+,
∴当x=3时,DF有最大值,
此时,点D的坐标为(3,3),
∴直线DE是由直线AC向右平移3个单位所得,
设直线AC的解析式为y=mx+n,
则,解得:,
∴直线AC的解析式为y=x+3,
∴直线DE的解析式为y=x+3﹣3=x,
联立直线DE的解析式和直线BC的解析式,得
,解得:,
∴点E的坐标为(2,2),
∴DE最大值=.
26.(1)8
(2)
(3)当t=3时,S的值最大.
(1)
解:当t=4时,则AP=4×1=4(mm),BQ=4×2=8(mm),
∴,
∴S=×2×8=8(平方毫米);
(2)
解:∵动点P从点A开始沿边AB向点B以1mm/s的速度移动,动点Q从点B开始沿边BC向点C以2mm/s的速度移动,
∴BP=(6-t)(mm),BQ=2t(mm),
∴S=×BP×BQ=t×(6-t)=t2+6t(0<t≤6);
(3)
解:∵,
∴当t=3时,S的值最大.
答案第1页,共2页
一、单选题
1.函数是二次函数,函数有最大值,则a满足( )
A. B. C. D.a为任意实数
2.已知点(1,y1),(2,y2)都在函数y=﹣x2的图象上,则( )
A.y1<y2 B.y1>y2
C.y1=y2 D.y1,y2大小不确定
3.抛物线y=(x+3)2+2的对称轴是( )
A.直线x=3 B.直线x=-3 C.直线x=2 D.直线x=-2
4.抛物线的顶点坐标是( )
A. B. C. D.
5.抛物线y=ax2+bx+c(a<0)与x轴的一个交点坐标为(﹣2,0),对称轴为直线x=2,当y>0时,x的取值范围是( )
A.x>﹣2 B.x<6 C.﹣2<x<6 D.x<﹣2或x>6
6.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B的坐标为(1,0),下面的四个结论:① abc>0;② a-b+c<0;③ 2a-b=0;④3a+c>0.其中正确结论个数有( ).
A.1个 B.2个 C.3个 D.4个
7.抛物线沿x 轴向右平移2个单位后的顶点坐标是( ).
A.(0,2) B.(0,-2) C.(2,0) D.(-2,0)
8.抛物线向左平移2个单位,再向上平移5个单位,所得抛物线解析式为( )
A. B.
C. D.
9.对于二次函数y= 3(x 1)2+5,下列说法正确的是( )
A.函数图象的开口向上 B.函数图象的对称轴为直线
C.函数的最小值为5 D.当时,y随x的增大而增大
10.已知点在二次函数的图象上,且C为抛物线的顶点.若,则m的取值范围是( )
A. B. C. D.
11.已知一抛物线与二次函数图象的开口大小相同,开口方向相同且顶点坐标为(-1,2021),则该抛物线对应的函数表达式为( )
A. B.
C. D.
12.已知点在抛物线的图像上,且当时,;当或时,时.若,则m的值为( )
A.-1 B.3 C.-1或7 D.3或7
13.已知一次函数y=ax+b的图象如图所示,那么二次函数y=ax2+bx+1的图象大致为( )
A. B.
C. D.
14.对于二次函数y=,下列说法正确的是( )
A.该函数图象开口向上
B.该函数图象与y轴的交点为(2,0)
C.该函数有最小值且最小值为
D.当x>﹣1时,函数值y随x的增大而减小
15.已知二次函数,如果随的增大而增大,那么的取值范围是( )
A. B. C. D.
16.二次函数与一次函数在同一直角坐标系中图象大致是( )
A.B.C. D.
二、填空题
17.任意写出一个顶点坐标是(2,-3)的二次函数解析式______.
18.如果抛物线y=﹣m(x+1)2﹣m+1的顶点坐标为(﹣1,2),那么它的开口方向 _____.
19.二次函数的图象上最低点的坐标是_____.
20.二次函数的图象经过点,则代数式的值为__________.
21.如图,为一块铁板余料,BC=10cm,高AD=10cm,要用这块余料裁出一个矩形PQMN,使矩形的顶点P、N分别在边AB,AC上.顶点Q,M在边BC上,则矩形PQMN面积的最大值为_____.
三、解答题
22.已知二次函数y=x2+3mx+1﹣m的图象与x轴的一个交点为(2,0).
(1)求m的值;
(2)求这个函数图象与x轴另一个交点的横坐标.
23.如图,直线与抛物线交于,两点,与轴于点,其中点的坐标为.
(1)求,的值;
(2)若于点,.试说明点在抛物线上.
24.设二次函数y=(mx﹣2)(x﹣2m),其中m是常数.
(1)当m=2时,试判断点(1,0)是否在该函数图象上;
(2)用含m的代数式表示函数的对称轴;
(3)当x≥﹣2时,y随x的增大而减小,求m的范围
25.如图,二次函数的图象交x轴于A,B两点,交y轴于点C,点D是BC上方抛物线上的一点,过D作AC的平行线,交BC于点E.
(1)求△ABC的面积;
(2)连接CD,当CD∥x轴时,求△CDE的面积;
(3)求DE的最大值.
26.如图,在ABC中,∠B=90°,AB=6mm,BC=12mm,动点P从点A开始沿边AB向点B以1mm/s的速度移动,动点Q从点B开始沿边BC向点C以2mm/s的速度移动,且与点P同时出发.设PBQ的面积为S,动点移动的时间为t(t>0).
(1)当t=4时,求S的值;
(2)求S关于t的函数解析式;
(3)t为何值时,S的值最大?
试卷第1页,共3页
参考答案:
1.A
解:当抛物线开口向下,在顶点处产生最大值,
故,
故A符合题意,B、C、D不符合题意,
故选:A.
2.B
解:∵点(1,y1),(2,y2)都在函数y=﹣x2的图象上,
∴,,
∴,
故选B.
3.B
解:抛物线y=(x+3)2+2的顶点坐标为(-3,2),
故该抛物线的对称轴是直线x=-3.
故选:B.
4.A
解:∵,
∴此函数的顶点坐标为(3,1),
故选:A.
5.C
解:∵抛物线对称轴为直线x=2,与x轴一个交点坐标为(-2,0),
∴抛物线与x轴另一交点坐标为(6,0),
∴当y>0时,x的取值范围是﹣2
6.B
解:,
∴,
∵抛物线开口向上,a>0,
∴>0,
抛物线y=ax2+bx+c(a≠0)的图象与y轴交点在y轴负半轴,
∴c<0,
∴abc<0,
故①不正确;
当x=﹣1时,y=a﹣b+c函数值为负数,
∴a﹣b+c<0,
故②正确;
∵,
∴,
故③正确;
∵点B的坐标为(1,0),
∴,
∵,
∴,
故④不正确;
综上②③正确,只有两个,
故选:B
7.C
解:∵抛物线的顶点坐标为(0,0),
则平移后抛物线为,顶点坐标为(2,0)
∴向右平移2个单位后的顶点坐标是(2,0).
故选C.
8.D
解:∵抛物线向左平移2个单位,再向上平移5个单位,
∴所得抛物线解析式为
故选D
9.D
解:二次函数y=-3(x-1)2+5
∵-3<0,
∴二次函数的的图象的开口向下,对称轴为直线x=1,最大值为5,
当x<1时,y随x的增大而增大,
故选:D.
10.B
解:抛物线的对称轴为直线
点C为抛物线的顶点
点C为抛物线的最低点,即抛物线开口向上
点
,
故选:B.
11.D
解:∵抛物线与二次函数图象的开口大小相同,开口方向相同且顶点坐标为(-1,2021),
∴该抛物线对应的函数表达式为.
故选:D
12.C
解:由题意可得抛物线对称轴为直线,且开口向下,
,,
,
点在抛物线上,
,
,
,
解得或,
故选:C.
13.B
解:∵y=ax+b的图象经过一、二、三象限,
∴a>0,b>0,
∴﹣<0,
∴二次函数y=ax2+bx+1的图象开口向上,对称轴在y轴的左侧,交y轴的正半轴.
故选:B
14.D
解:∵
∴
∴该函数图象开口向下
故A选项错误;
∵当x=0时,y=2,
∴函数图象与y轴的交点为(0,2)
故B选项错误;
∵,
∴该函数有最大值且最大值为
故C选项错误;
∵该抛物线的对称轴为:直线,图象开口向下
∴当x>﹣1时,函数值y随x的增大而减小.
故D选项正确.
故选:D.
15.A
解:
抛物线开口方向向下,对称轴为直线
当时,随的增大而增大.
故选:A.
16.A
解:A.图象中二次函数,一次函数,故A符合题意.
B.图象中二次函数,一次函数,故B不符合题意.
C.图象中二次函数,一次函数,故C不符合题意.
D.图象中二次函数,一次函数,故D不符合题意.
故选:A.
17.(答案不唯一)
解:满足顶点坐标是的二次函数解析式为,
故答案为:(答案不唯一).
18.向上
解:∵抛物线的顶点坐标为(-1,2),
∴,
∴,
∴抛物线解析式为,
∴抛物线的开口向上,
故答案为:向上.
19.
解:对于二次函数,
当时,随的增大而减小;当时,随的增大而增大,
所以此二次函数的顶点即为图象上的最低点,
因为二次函数的顶点坐标为,
所以此函数图象上最低点的坐标是,
故答案为:.
20.﹣1
解:∵二次函数y=ax2+bx﹣1(a≠0)的图象经过点(﹣1,1),
∴a﹣b﹣1=1,
∴1﹣a+b
=﹣(a﹣b﹣1)
=﹣1.
故答案为:﹣1
21.25
解:设DE=x,
∵四边形PQMN是矩形,AD⊥BC,
∴,PQ=MN=DE,
∴△APN∽△ABC,
∴,
∴,
∴PN=10-x,
∴矩形PQMN面积=,
∴当x=5时,矩形PQMN面积有最大值,最大值为25cm2,
故答案为:25.
.
22.(1);
(2)函数图象与x轴另一个交点的横坐标为1
(1)
∵二次函数y=x2+3mx+1﹣m的图象与x轴的一个交点为(2,0),
∴4+6m+1﹣m=0,
解得:m=﹣1;
(2)
由(1)得:二次函数解析式为y=x2﹣3x+2,
令y=0,则x2﹣3x+2=0,
解得:x1=1,x2=2,
∴函数图象与x轴另一个交点的横坐标为1.
23.(1),
(2)见解析
(1)
把点A(-4,8)代入,得:
∴;
把点A(-4,8)代入,得:
∴;
(2)
如图,分别过点A,D作AM⊥y轴于点M,DN⊥y轴于点N.
∵直线AB的解析式为y=-x+6,
令x=0,则y=6
∴C(0,6),
∵∠AMC=∠DNC=∠ACD=90°,
∴∠ACM+∠DCN=90°,∠DCN+∠CDN=90°,
∴∠ACM=∠CDN,
∵CA=CD,
∴△AMC≌△CND(SAS),
∴CN=AM=4,DN=CM=2,
∴D(-2,2),
当x=-2时,y=×22=2,
∴点D在抛物线y=x2上.
24.(1)(1,0)在该函数图象上
(2)x
(3)m≤﹣2
(1)
解:当m=2时,y=(2x﹣2)(x﹣4),
取x=1,则y=(2﹣2)×(1﹣2)=0,
∴(1,0)在该函数图象上;
(2)
∵y=(mx﹣2)(x﹣2m),
∴函数图象与x轴的交点为,,
∴抛物线的对称轴为x=;
(3)
∵当x≥﹣2时,y随x的增大而减小,
∴,
解得m≤﹣2,
∴m的范围为m≤﹣2.
25.(1);
(2);
(3)
(1)
解:当x=0时,y=3,
∴C(0,3),OC=3,
当y=0时,﹣x2+x+3=0,
解得:x=﹣3或x=6,
∴A(﹣3,0),B(6,0),
∴AB=9,
∴S△ABC=.
(2)
解:∵C(0,3),CD∥x轴,
∴D(3,3),∠DCE=∠ABC,
∴CD=3,
∵DE∥AC,
∴∠DEC=∠ACB,
∴△DEC∽△ACB,
∴,
∵S△ABC=,
∴S△DEC=.
(3)
解:如图,过点D作DF∥y轴交BC于点F,过点E作EH⊥DF于点H,
∵DE∥AC,DF∥y轴,
∴∠DEF的度数不变,∠EFD的度数不变,
∴在点D的移动过程中△DEF的形状保持不变,
∴当DF最大时,DE的长度也最大,
设直线BC的解析式为y=kx+b,
则,解得:,
∴直线BC的解析式为y=﹣x+3,
设点D的坐标(x,﹣x2+x+3),则点F的坐标(x,﹣x+3),
∴DF=﹣x2+x+3﹣(﹣x+3)=﹣x2+x=﹣(x﹣3)2+,
∴当x=3时,DF有最大值,
此时,点D的坐标为(3,3),
∴直线DE是由直线AC向右平移3个单位所得,
设直线AC的解析式为y=mx+n,
则,解得:,
∴直线AC的解析式为y=x+3,
∴直线DE的解析式为y=x+3﹣3=x,
联立直线DE的解析式和直线BC的解析式,得
,解得:,
∴点E的坐标为(2,2),
∴DE最大值=.
26.(1)8
(2)
(3)当t=3时,S的值最大.
(1)
解:当t=4时,则AP=4×1=4(mm),BQ=4×2=8(mm),
∴,
∴S=×2×8=8(平方毫米);
(2)
解:∵动点P从点A开始沿边AB向点B以1mm/s的速度移动,动点Q从点B开始沿边BC向点C以2mm/s的速度移动,
∴BP=(6-t)(mm),BQ=2t(mm),
∴S=×BP×BQ=t×(6-t)=t2+6t(0<t≤6);
(3)
解:∵,
∴当t=3时,S的值最大.
答案第1页,共2页
