5.4 抛体运动的规律 同步练习题(Word版含答案)
文档属性
| 名称 | 5.4 抛体运动的规律 同步练习题(Word版含答案) | 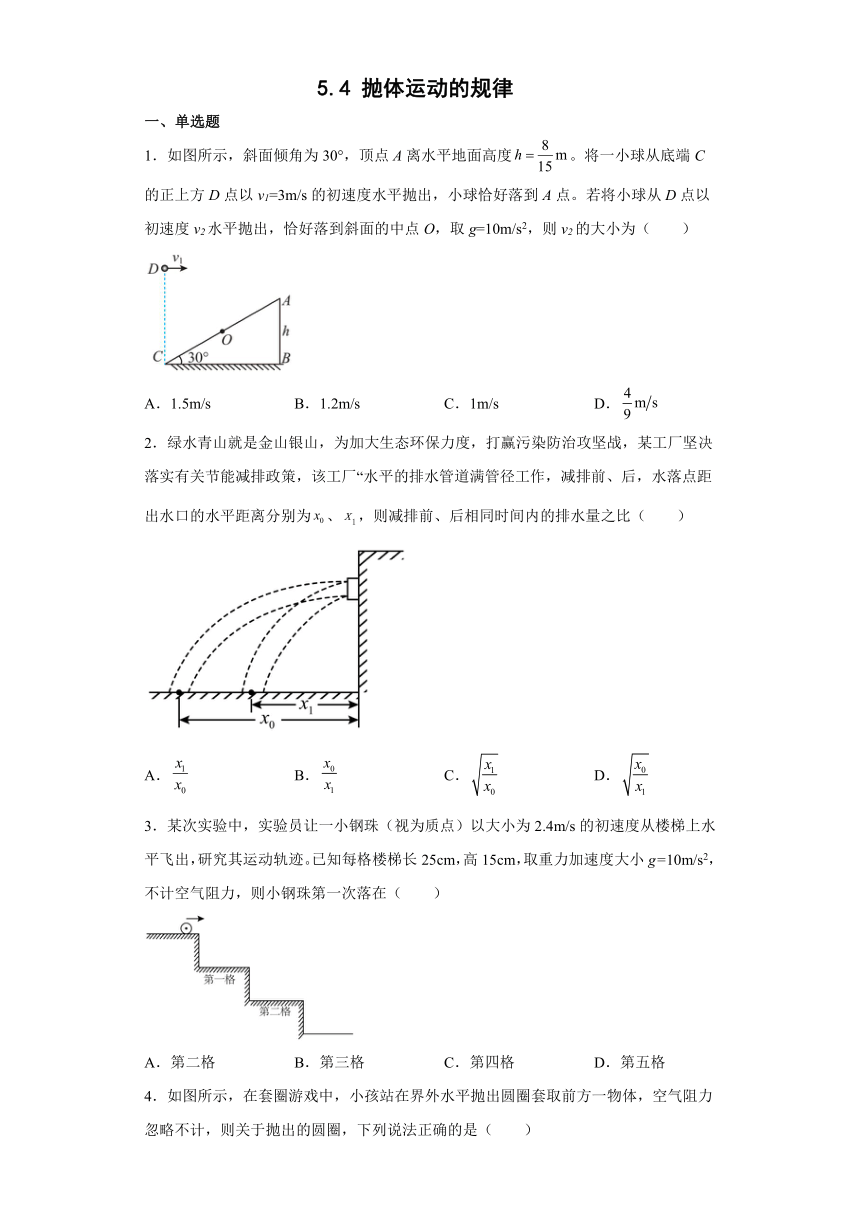 | |
| 格式 | doc | ||
| 文件大小 | 966.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-13 17:45:51 | ||
图片预览




文档简介
5.4 抛体运动的规律
一、单选题
1.如图所示,斜面倾角为30°,顶点A离水平地面高度。将一小球从底端C的正上方D点以v1=3m/s的初速度水平抛出,小球恰好落到A点。若将小球从D点以初速度v2水平抛出,恰好落到斜面的中点O,取g=10m/s2,则v2的大小为( )
A.1.5m/s B.1.2m/s C.1m/s D.
2.绿水青山就是金山银山,为加大生态环保力度,打赢污染防治攻坚战,某工厂坚决落实有关节能减排政策,该工厂“水平的排水管道满管径工作,减排前、后,水落点距出水口的水平距离分别为、,则减排前、后相同时间内的排水量之比( )
A. B. C. D.
3.某次实验中,实验员让一小钢珠(视为质点)以大小为2.4m/s的初速度从楼梯上水平飞出,研究其运动轨迹。已知每格楼梯长25cm,高15cm,取重力加速度大小g=10m/s2,不计空气阻力,则小钢珠第一次落在( )
A.第二格 B.第三格 C.第四格 D.第五格
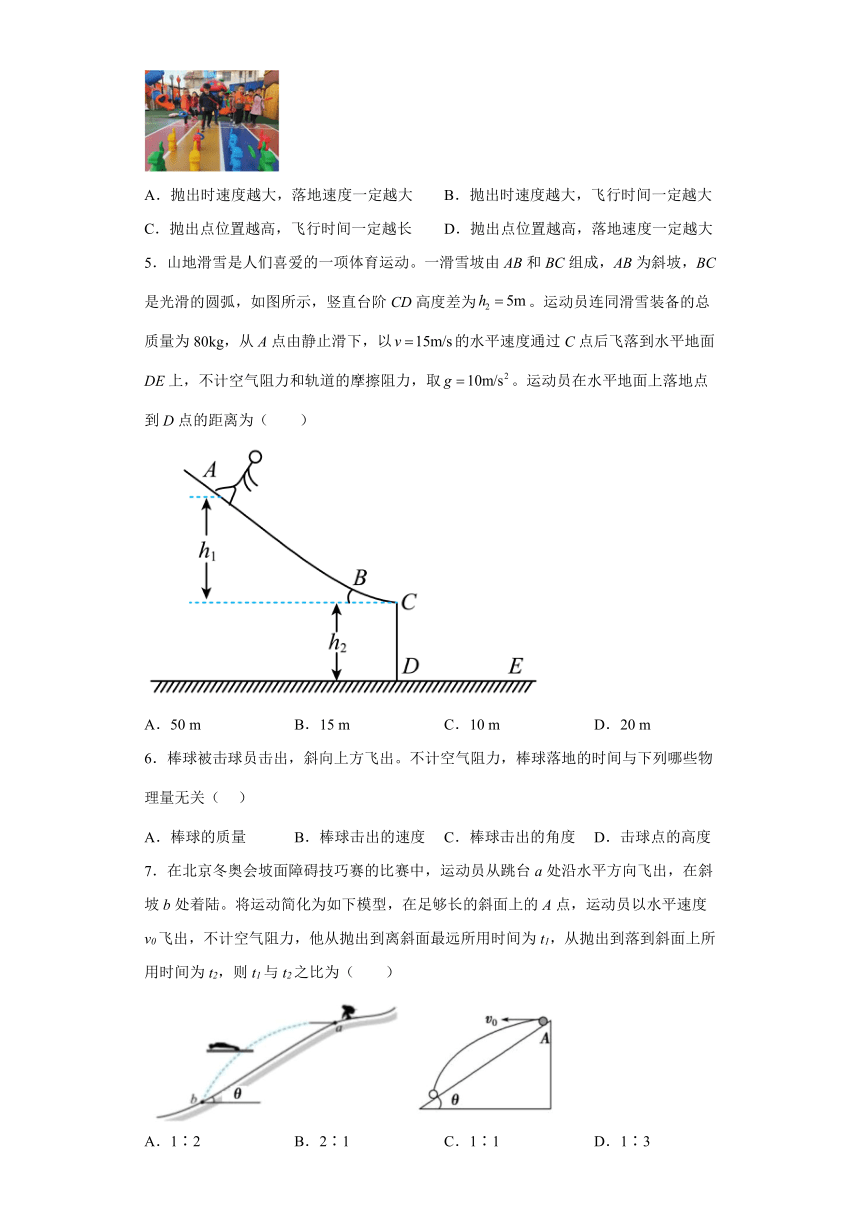
4.如图所示,在套圈游戏中,小孩站在界外水平抛出圆圈套取前方一物体,空气阻力忽略不计,则关于抛出的圆圈,下列说法正确的是( )
A.抛出时速度越大,落地速度一定越大 B.抛出时速度越大,飞行时间一定越大
C.抛出点位置越高,飞行时间一定越长 D.抛出点位置越高,落地速度一定越大
5.山地滑雪是人们喜爱的一项体育运动。一滑雪坡由AB和BC组成,AB为斜坡,BC是光滑的圆弧,如图所示,竖直台阶CD高度差为。运动员连同滑雪装备的总质量为80kg,从A点由静止滑下,以的水平速度通过C点后飞落到水平地面DE上,不计空气阻力和轨道的摩擦阻力,取。运动员在水平地面上落地点到D点的距离为( )
A.50 m B.15 m C.10 m D.20 m
6.棒球被击球员击出,斜向上方飞出。不计空气阻力,棒球落地的时间与下列哪些物理量无关( )
A.棒球的质量 B.棒球击出的速度 C.棒球击出的角度 D.击球点的高度
7.在北京冬奥会坡面障碍技巧赛的比赛中,运动员从跳台a处沿水平方向飞出,在斜坡b处着陆。将运动简化为如下模型,在足够长的斜面上的A点,运动员以水平速度v0飞出,不计空气阻力,他从抛出到离斜面最远所用时间为t1,从抛出到落到斜面上所用时间为t2,则t1与t2之比为( )
A.1∶2 B.2∶1 C.1∶1 D.1∶3
二、多选题
8.关于平抛运动,下列说法正确的是( )
A.平抛运动是匀变速曲线运动
B.做平抛运动的物体在任何相等的时间内,速度的变化量都相等
C.可以分解为水平方向的匀速直线运动和竖直方向上的自由落体运动
D.落地时间和落地时的速度只与抛出点的高度有关
9.将某物体以的初速度水平抛出,不计空气阻力,当其竖直分速度与水平分速度大小相等时,已知重力加速度为g,下列说法中正确的是( )
A.竖直分位移与水平分位移大小之比为1∶1 B.此过程所用的时间为
C.运动位移的大小为 D.运动位移的大小为
10.刀削面是西北人喜欢的面食之一,全凭刀削得名。如图所示,将一锅水烧开,拿一块面团放在锅旁边较高处,用一刀片飞快地削下一片片很薄的面片,面片便水平飞向锅里。若面团到锅的上沿的竖直距离始终为0.8m,面团离锅上沿最近的水平距离为0.4m,锅的半径为0.4m,若削出的面片落入锅中,则面片的初速度可能是()( )
A.3.2m/s B.1.6m/s C.1.8m/s D.2.5m/s
11.2020年2月,在国际单板滑雪U型场地赛中,我国运动员蔡雪桐勇夺冠军。如图,滑道边缘线PQ的倾角为θ,运动员以速度v0从PQ上的O点沿PQ的竖直切面滑出滑道,滑出时速度方向与PQ的夹角为α,腾空后从PQ上的A点进入滑道。已知=90°,重力加速度为g,运动员可视为质点,不计空气阻力,下列说法正确的是( )
A.O、A两点间的距离为
B.运动员腾空中离PQ的最大距离为
C.若仅减小夹角,则运动员腾空时间可能保持不变
D.若仅增大v0的大小,则运动员再滑入轨道的速度方向不变
12.将一只小球水平抛出,小球在空中依次飞过1号、2号、3号三个完全相同的窗户,图中曲线为小球在空中运行的轨迹。若不计空气阻力的影响,以下说法正确的是( )
A.小球通过3号窗户所用的时间最长
B.小球通过1号窗户所用的时间最长
C.小球通过3个窗户速度的变化一样快
D.3个窗户所截得的小球运动轨迹相同
三、填空题
13.乒乓球运动是同学们喜欢的一个运动项目,现将一个乒乓球从1.25m的高处以2m/s的水平初速度抛出,不考虑空气阻力,该乒乓球在空中运动的时间t=___________s,水平运动的距离x=___________m。
14.宇航员登陆某星球做了一个平抛运动实验,并用频闪照相机记录小球做平抛运动的部分轨迹,且已知平抛初速度为5 m/s。将相片放大到实际大小后在水平方向和竖直方向建立平面直角坐标系,A、B、C为小球运动中的3个连续的记录点,A、B和C点的坐标分别为(0 m,0 m)(0.50 m,0.20 m)和(1.00 m,0.60 m)。则:
(1)频闪照相机的频闪频率为________ Hz;
(2)该星球表面重力加速度为________ m/s2;
(3)小球开始做平抛运动的初始位置坐标为x=________ m,y=________ m。
15.如图所示,等腰直角三角形ABC为固定斜面的竖直截面,将小球自A点正上方某处由静止释放,小球与斜面发生无能量损失的碰撞后水平弹出,并恰好落到B点。已知AC=h,重力加速度为g,则P、A之间的高度差为_______________。
四、解答题
16.悬崖上平抛一物体,当抛出时它的速度方向与水平方的夹角为,落地时速度偏转角正切值为2,不计空气阻力:取,求。
(1)初速度大小;
(2)落地速度大小;
(3)悬崖的高度。
17.第24届冬季奥林匹克运动会将于2022年在北京和张家口联合举办。冬奥会上跳台滑雪是一种勇敢者的滑雪运动,运动员穿专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在空中飞行一段距离后着陆。现有某运动员从跳台a处沿水平方向飞出,速度大小v0=20m/s,在斜坡b处着陆,如图所示。斜坡与水平方向的夹角为37°,不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8。求:
(1)运动员在空中飞行的时间t;
(2)斜坡上a、b之间的距离s;
(3)运动员在空中离坡面的最大距离d。
18.如图是一种加速度测量仪的装置示意图。在小车上方竖直固定一根杆OO’,顶端O’处的盒子中有一小球(可视为质点),小球随车一起沿水平地面做匀加速直线运动。某时刻小球从盒中释放,且小球释放瞬间与小车具有相同的水平速度v0(未知),小球释放后对小车运动无影响,最终小球落在小车上表面的刻度尺AB之间。利用固定的白纸、复写纸记录小球的初始落点P(未画出),读出OP的距离x。已知小车速度平行于刻度尺AB,杆长OO’=9.8cm,x=3.6cm,重力加速度g=9.8m/s2,不计空气阻力。则:
(1)若落点P在O点右侧,则小车在向左加速还是向右加速运动;(直接给出答案即可)
(2)求出小车的加速度大小;
(3)若在刻度尺上直接标记小球不同落点时的对应小车加速度,则该“加速度尺”的刻度是否均匀。(请说明理由)
19.棒球运动是一项集智慧与勇敢、趣味与协作于一体的集体运动项目,深受青少年喜爱。如图所示,某次投手在点将球水平抛向捕手,捕手预备在点接球,击球员预备在点击球。棒球可看作质点,空气阻力不计。已知:点离地面1.8米,点离地面1.0米,、两点的水平距离为20米,球抛出后经0.5秒到达点,取。求:
(1)棒球抛出后到达点的时间;
(2)棒球被抛出时的速度大小;
(3)若击球员和捕手均未碰到球,棒球落地时的速度方向。
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
设C、D两点的高度差为H,当小球落到A点,由平抛运动规律得
,
小球落到O点,由平抛运动规律得
,
解得
v2=1.2m/s
故B正确,ACD错误。
故选B。
2.B
【解析】
【详解】
设水下落的高度为h与水下落的时间关系为
故下落高度相同,水流入下方的时间相同
根据平抛运动水平方向的位移与时间关系
减排前、后水的流速比就等于水平位移之比
所以减排前、后相同时间内的排水量之比就等于水平位移之比即,ACD错误,B正确。
故选B。
3.B
【解析】
【详解】
设小钢球落到第n格,则由平抛规律可得
解得
这里n取大于2.7648的整数,所以n=3。即小球落到第三格。
故选B。
4.C
【解析】
【详解】
BC.由平抛运动规律
解得飞行时间
可知抛出点位置越高,飞行时间越长,与抛出速度无关,故B错误,C正确;
AD.落地速度
即落地速度与抛出高度和抛出速度均有关,其中一个量大,落地速度不一定大,故AD错误。
故选C。
5.B
【解析】
【详解】
运动员离开C点后做平抛运动,竖直方向
水平位移
故ACD错误,B正确。
故选B。
6.A
【解析】
【详解】
设棒球与水平方向的夹角为,可得
故可知棒球落地的时间与棒球击出的速度、棒球击出的角度、击球点的高度有关,与棒球的质量无关,BCD错误,A正确。
故选A。
7.A
【解析】
【详解】
从抛出到离斜面最远时速度方向与斜面平行,速度夹角为,即
从抛出到落到斜面上时,位移夹角为,即
所以有
解得
故A正确,BCD错误。
故选A。
8.ABC
【解析】
【分析】
【详解】
A.平抛运动只受重力作用,加速度为g,是个定值,所以平抛运动是匀变速曲线运动,A正确;
BC.平抛运动可以分解为水平方向的匀速直线运动和竖直方向上的自由落体运动,则加速度为g,根据
BC正确;
D.根据
落地时间只与抛出点的高度有关,落地速度
与水平初速度v0及抛出点高度都有关,D错误。
故选ABC。
9.BC
【解析】
【详解】
B.竖直分速度与水平分速度大小相等时有
v0= gt
解得
B正确;
A.竖直分位移和水平分位移分别为
,
则
y:x = 1:2
A错误;
CD.根据位移的矢量合成,结合选项A有
C正确、D错误。
故选BC。
10.BCD
【解析】
【详解】
根据平抛运动的公式,水平方向有
x=v0t
竖直方向有
其中
联立可得
故选BCD。
11.AD
【解析】
【详解】
AB.将初速度v0和加速度g分别分解在沿斜面方向和垂直斜面方向,则垂直斜面方向
运动员腾空中离PQ的最大距离为
O、A两点间的距离为
选项A正确,B错误;
C .运动员腾空时间
若仅减小夹角,则运动员腾空时间减小,选项C错误;
D.运动员再滑入轨道时,垂直斜面方向的速度不变,仍为
v1=v0cosθ
沿斜面向下的速度
则合速度与斜面的夹角
与初速度无关,则选项D正确。
故选AD。
12.BC
【解析】
【详解】
AB.根据平抛运动规律,小球通过窗户所用的时间决定于竖直方向的分速度,而小球在竖直方向上做自由落体运动,速度越来越大,故可知,通过三个窗户所用的时间t1>t2>t3,故选项B正确,A错误;
C.因为加速度相同,所以小球通过3个窗户速度的变化一样快,选项C正确;
D.由平抛规律可知,合速度的方向不同,故运动轨迹不同,选项D错误。
故选BC。
13. 0.5 1
【解析】
【详解】
乒乓球在竖直方向做自由落体运动,根据
解得
水平方向运动的距离
14. 10 20 -0.25 -0.025
【解析】
【详解】
(1).频闪照相机的频闪频率为
(2)根据△y=gT2可得
(3)B点的竖直速度
则抛出点到B点的竖直距离
到达B点的时间
则抛出点的纵坐标
y=-(0.225-0.20)m=-0.025m
抛出点的横坐标为
x=-(v0tB-xB)=-(5×0.15-0.5)m=-0.25m
15.
【解析】
【详解】
设小球到达A点速度为v0,则
然后做平抛运动,根据几何关系知
且
联立解得
16.(1) ;(2) ;(3)
【解析】
【分析】
【详解】
(1) 当抛出时,竖直方向的速度为
则由
可得
(2)由
可得
落地速度大小
(3)悬崖的高度为
17.(1)3s;(2)75m;(3)9m
【解析】
【详解】
(1)运动员做平抛运动,设着陆时间为t,则有
x=v0t
由图可知,运动员着陆时
tan=
可解得
(2)运动员着陆时
x=v0t=60m
所以
=75m
(3)取沿斜坡向下方向(x方向)与垂直于斜坡向上方向(y方向)分析运动员的运动,则在垂直于斜坡方向上
vy=v0sin=12m/s,ay=-gcos=-8m/s2
当vy=0时,运动员在空中离坡面的距离最大,则有
18.(1)小车向左加速运动;(2)a=3.6m/s2;(3)刻度均匀
【解析】
【详解】
(1)车做加速运动,小球水平方向为匀速运动,初速度相同的情况下,显然小车水平位移更大,P点在O点右侧说明小车向左加速运动;
(2)水平方向上,小球
x1=v0t
小车
x2=v0t+
相对位移
x=x2-x1=
竖直方向上
h=
联立得
即
(3)由可知,相对位移与加速度成正比,故刻度均匀。
19.(1)0.4s;(2)40m/s;(3)速度方向与水平方向的夹角正切值
【解析】
【详解】
(1)从A到C竖直高度为
根据
解得到达点的时间
(2)从A到B水平方向,根据
解得
(3)从A到B落地时竖直方向的速度
解得
则棒球落地时的速度方向与水平方向的夹角
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,斜面倾角为30°,顶点A离水平地面高度。将一小球从底端C的正上方D点以v1=3m/s的初速度水平抛出,小球恰好落到A点。若将小球从D点以初速度v2水平抛出,恰好落到斜面的中点O,取g=10m/s2,则v2的大小为( )
A.1.5m/s B.1.2m/s C.1m/s D.
2.绿水青山就是金山银山,为加大生态环保力度,打赢污染防治攻坚战,某工厂坚决落实有关节能减排政策,该工厂“水平的排水管道满管径工作,减排前、后,水落点距出水口的水平距离分别为、,则减排前、后相同时间内的排水量之比( )
A. B. C. D.
3.某次实验中,实验员让一小钢珠(视为质点)以大小为2.4m/s的初速度从楼梯上水平飞出,研究其运动轨迹。已知每格楼梯长25cm,高15cm,取重力加速度大小g=10m/s2,不计空气阻力,则小钢珠第一次落在( )
A.第二格 B.第三格 C.第四格 D.第五格
4.如图所示,在套圈游戏中,小孩站在界外水平抛出圆圈套取前方一物体,空气阻力忽略不计,则关于抛出的圆圈,下列说法正确的是( )
A.抛出时速度越大,落地速度一定越大 B.抛出时速度越大,飞行时间一定越大
C.抛出点位置越高,飞行时间一定越长 D.抛出点位置越高,落地速度一定越大
5.山地滑雪是人们喜爱的一项体育运动。一滑雪坡由AB和BC组成,AB为斜坡,BC是光滑的圆弧,如图所示,竖直台阶CD高度差为。运动员连同滑雪装备的总质量为80kg,从A点由静止滑下,以的水平速度通过C点后飞落到水平地面DE上,不计空气阻力和轨道的摩擦阻力,取。运动员在水平地面上落地点到D点的距离为( )
A.50 m B.15 m C.10 m D.20 m
6.棒球被击球员击出,斜向上方飞出。不计空气阻力,棒球落地的时间与下列哪些物理量无关( )
A.棒球的质量 B.棒球击出的速度 C.棒球击出的角度 D.击球点的高度
7.在北京冬奥会坡面障碍技巧赛的比赛中,运动员从跳台a处沿水平方向飞出,在斜坡b处着陆。将运动简化为如下模型,在足够长的斜面上的A点,运动员以水平速度v0飞出,不计空气阻力,他从抛出到离斜面最远所用时间为t1,从抛出到落到斜面上所用时间为t2,则t1与t2之比为( )
A.1∶2 B.2∶1 C.1∶1 D.1∶3
二、多选题
8.关于平抛运动,下列说法正确的是( )
A.平抛运动是匀变速曲线运动
B.做平抛运动的物体在任何相等的时间内,速度的变化量都相等
C.可以分解为水平方向的匀速直线运动和竖直方向上的自由落体运动
D.落地时间和落地时的速度只与抛出点的高度有关
9.将某物体以的初速度水平抛出,不计空气阻力,当其竖直分速度与水平分速度大小相等时,已知重力加速度为g,下列说法中正确的是( )
A.竖直分位移与水平分位移大小之比为1∶1 B.此过程所用的时间为
C.运动位移的大小为 D.运动位移的大小为
10.刀削面是西北人喜欢的面食之一,全凭刀削得名。如图所示,将一锅水烧开,拿一块面团放在锅旁边较高处,用一刀片飞快地削下一片片很薄的面片,面片便水平飞向锅里。若面团到锅的上沿的竖直距离始终为0.8m,面团离锅上沿最近的水平距离为0.4m,锅的半径为0.4m,若削出的面片落入锅中,则面片的初速度可能是()( )
A.3.2m/s B.1.6m/s C.1.8m/s D.2.5m/s
11.2020年2月,在国际单板滑雪U型场地赛中,我国运动员蔡雪桐勇夺冠军。如图,滑道边缘线PQ的倾角为θ,运动员以速度v0从PQ上的O点沿PQ的竖直切面滑出滑道,滑出时速度方向与PQ的夹角为α,腾空后从PQ上的A点进入滑道。已知=90°,重力加速度为g,运动员可视为质点,不计空气阻力,下列说法正确的是( )
A.O、A两点间的距离为
B.运动员腾空中离PQ的最大距离为
C.若仅减小夹角,则运动员腾空时间可能保持不变
D.若仅增大v0的大小,则运动员再滑入轨道的速度方向不变
12.将一只小球水平抛出,小球在空中依次飞过1号、2号、3号三个完全相同的窗户,图中曲线为小球在空中运行的轨迹。若不计空气阻力的影响,以下说法正确的是( )
A.小球通过3号窗户所用的时间最长
B.小球通过1号窗户所用的时间最长
C.小球通过3个窗户速度的变化一样快
D.3个窗户所截得的小球运动轨迹相同
三、填空题
13.乒乓球运动是同学们喜欢的一个运动项目,现将一个乒乓球从1.25m的高处以2m/s的水平初速度抛出,不考虑空气阻力,该乒乓球在空中运动的时间t=___________s,水平运动的距离x=___________m。
14.宇航员登陆某星球做了一个平抛运动实验,并用频闪照相机记录小球做平抛运动的部分轨迹,且已知平抛初速度为5 m/s。将相片放大到实际大小后在水平方向和竖直方向建立平面直角坐标系,A、B、C为小球运动中的3个连续的记录点,A、B和C点的坐标分别为(0 m,0 m)(0.50 m,0.20 m)和(1.00 m,0.60 m)。则:
(1)频闪照相机的频闪频率为________ Hz;
(2)该星球表面重力加速度为________ m/s2;
(3)小球开始做平抛运动的初始位置坐标为x=________ m,y=________ m。
15.如图所示,等腰直角三角形ABC为固定斜面的竖直截面,将小球自A点正上方某处由静止释放,小球与斜面发生无能量损失的碰撞后水平弹出,并恰好落到B点。已知AC=h,重力加速度为g,则P、A之间的高度差为_______________。
四、解答题
16.悬崖上平抛一物体,当抛出时它的速度方向与水平方的夹角为,落地时速度偏转角正切值为2,不计空气阻力:取,求。
(1)初速度大小;
(2)落地速度大小;
(3)悬崖的高度。
17.第24届冬季奥林匹克运动会将于2022年在北京和张家口联合举办。冬奥会上跳台滑雪是一种勇敢者的滑雪运动,运动员穿专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在空中飞行一段距离后着陆。现有某运动员从跳台a处沿水平方向飞出,速度大小v0=20m/s,在斜坡b处着陆,如图所示。斜坡与水平方向的夹角为37°,不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8。求:
(1)运动员在空中飞行的时间t;
(2)斜坡上a、b之间的距离s;
(3)运动员在空中离坡面的最大距离d。
18.如图是一种加速度测量仪的装置示意图。在小车上方竖直固定一根杆OO’,顶端O’处的盒子中有一小球(可视为质点),小球随车一起沿水平地面做匀加速直线运动。某时刻小球从盒中释放,且小球释放瞬间与小车具有相同的水平速度v0(未知),小球释放后对小车运动无影响,最终小球落在小车上表面的刻度尺AB之间。利用固定的白纸、复写纸记录小球的初始落点P(未画出),读出OP的距离x。已知小车速度平行于刻度尺AB,杆长OO’=9.8cm,x=3.6cm,重力加速度g=9.8m/s2,不计空气阻力。则:
(1)若落点P在O点右侧,则小车在向左加速还是向右加速运动;(直接给出答案即可)
(2)求出小车的加速度大小;
(3)若在刻度尺上直接标记小球不同落点时的对应小车加速度,则该“加速度尺”的刻度是否均匀。(请说明理由)
19.棒球运动是一项集智慧与勇敢、趣味与协作于一体的集体运动项目,深受青少年喜爱。如图所示,某次投手在点将球水平抛向捕手,捕手预备在点接球,击球员预备在点击球。棒球可看作质点,空气阻力不计。已知:点离地面1.8米,点离地面1.0米,、两点的水平距离为20米,球抛出后经0.5秒到达点,取。求:
(1)棒球抛出后到达点的时间;
(2)棒球被抛出时的速度大小;
(3)若击球员和捕手均未碰到球,棒球落地时的速度方向。
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
设C、D两点的高度差为H,当小球落到A点,由平抛运动规律得
,
小球落到O点,由平抛运动规律得
,
解得
v2=1.2m/s
故B正确,ACD错误。
故选B。
2.B
【解析】
【详解】
设水下落的高度为h与水下落的时间关系为
故下落高度相同,水流入下方的时间相同
根据平抛运动水平方向的位移与时间关系
减排前、后水的流速比就等于水平位移之比
所以减排前、后相同时间内的排水量之比就等于水平位移之比即,ACD错误,B正确。
故选B。
3.B
【解析】
【详解】
设小钢球落到第n格,则由平抛规律可得
解得
这里n取大于2.7648的整数,所以n=3。即小球落到第三格。
故选B。
4.C
【解析】
【详解】
BC.由平抛运动规律
解得飞行时间
可知抛出点位置越高,飞行时间越长,与抛出速度无关,故B错误,C正确;
AD.落地速度
即落地速度与抛出高度和抛出速度均有关,其中一个量大,落地速度不一定大,故AD错误。
故选C。
5.B
【解析】
【详解】
运动员离开C点后做平抛运动,竖直方向
水平位移
故ACD错误,B正确。
故选B。
6.A
【解析】
【详解】
设棒球与水平方向的夹角为,可得
故可知棒球落地的时间与棒球击出的速度、棒球击出的角度、击球点的高度有关,与棒球的质量无关,BCD错误,A正确。
故选A。
7.A
【解析】
【详解】
从抛出到离斜面最远时速度方向与斜面平行,速度夹角为,即
从抛出到落到斜面上时,位移夹角为,即
所以有
解得
故A正确,BCD错误。
故选A。
8.ABC
【解析】
【分析】
【详解】
A.平抛运动只受重力作用,加速度为g,是个定值,所以平抛运动是匀变速曲线运动,A正确;
BC.平抛运动可以分解为水平方向的匀速直线运动和竖直方向上的自由落体运动,则加速度为g,根据
BC正确;
D.根据
落地时间只与抛出点的高度有关,落地速度
与水平初速度v0及抛出点高度都有关,D错误。
故选ABC。
9.BC
【解析】
【详解】
B.竖直分速度与水平分速度大小相等时有
v0= gt
解得
B正确;
A.竖直分位移和水平分位移分别为
,
则
y:x = 1:2
A错误;
CD.根据位移的矢量合成,结合选项A有
C正确、D错误。
故选BC。
10.BCD
【解析】
【详解】
根据平抛运动的公式,水平方向有
x=v0t
竖直方向有
其中
联立可得
故选BCD。
11.AD
【解析】
【详解】
AB.将初速度v0和加速度g分别分解在沿斜面方向和垂直斜面方向,则垂直斜面方向
运动员腾空中离PQ的最大距离为
O、A两点间的距离为
选项A正确,B错误;
C .运动员腾空时间
若仅减小夹角,则运动员腾空时间减小,选项C错误;
D.运动员再滑入轨道时,垂直斜面方向的速度不变,仍为
v1=v0cosθ
沿斜面向下的速度
则合速度与斜面的夹角
与初速度无关,则选项D正确。
故选AD。
12.BC
【解析】
【详解】
AB.根据平抛运动规律,小球通过窗户所用的时间决定于竖直方向的分速度,而小球在竖直方向上做自由落体运动,速度越来越大,故可知,通过三个窗户所用的时间t1>t2>t3,故选项B正确,A错误;
C.因为加速度相同,所以小球通过3个窗户速度的变化一样快,选项C正确;
D.由平抛规律可知,合速度的方向不同,故运动轨迹不同,选项D错误。
故选BC。
13. 0.5 1
【解析】
【详解】
乒乓球在竖直方向做自由落体运动,根据
解得
水平方向运动的距离
14. 10 20 -0.25 -0.025
【解析】
【详解】
(1).频闪照相机的频闪频率为
(2)根据△y=gT2可得
(3)B点的竖直速度
则抛出点到B点的竖直距离
到达B点的时间
则抛出点的纵坐标
y=-(0.225-0.20)m=-0.025m
抛出点的横坐标为
x=-(v0tB-xB)=-(5×0.15-0.5)m=-0.25m
15.
【解析】
【详解】
设小球到达A点速度为v0,则
然后做平抛运动,根据几何关系知
且
联立解得
16.(1) ;(2) ;(3)
【解析】
【分析】
【详解】
(1) 当抛出时,竖直方向的速度为
则由
可得
(2)由
可得
落地速度大小
(3)悬崖的高度为
17.(1)3s;(2)75m;(3)9m
【解析】
【详解】
(1)运动员做平抛运动,设着陆时间为t,则有
x=v0t
由图可知,运动员着陆时
tan=
可解得
(2)运动员着陆时
x=v0t=60m
所以
=75m
(3)取沿斜坡向下方向(x方向)与垂直于斜坡向上方向(y方向)分析运动员的运动,则在垂直于斜坡方向上
vy=v0sin=12m/s,ay=-gcos=-8m/s2
当vy=0时,运动员在空中离坡面的距离最大,则有
18.(1)小车向左加速运动;(2)a=3.6m/s2;(3)刻度均匀
【解析】
【详解】
(1)车做加速运动,小球水平方向为匀速运动,初速度相同的情况下,显然小车水平位移更大,P点在O点右侧说明小车向左加速运动;
(2)水平方向上,小球
x1=v0t
小车
x2=v0t+
相对位移
x=x2-x1=
竖直方向上
h=
联立得
即
(3)由可知,相对位移与加速度成正比,故刻度均匀。
19.(1)0.4s;(2)40m/s;(3)速度方向与水平方向的夹角正切值
【解析】
【详解】
(1)从A到C竖直高度为
根据
解得到达点的时间
(2)从A到B水平方向,根据
解得
(3)从A到B落地时竖直方向的速度
解得
则棒球落地时的速度方向与水平方向的夹角
答案第1页,共2页
答案第1页,共2页
