五年级数学下册课件 3的倍数 特征 苏教版(共19张PPT)
文档属性
| 名称 | 五年级数学下册课件 3的倍数 特征 苏教版(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 544.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-13 06:41:04 | ||
图片预览





文档简介
(共19张PPT)
3 的倍数的特征
五年级数学下册
教学目标:
1、通过观察,探索,验证等活动,让学生经历发现3的倍数特征的过程,培养学生自主探索,合作交流的良好习惯;
2、理解并掌握3的倍数特征,并能熟练的用3的倍数特征解决实际问题。
3、让学生在探索过程中感受数学的奥妙,在运用规律中体现数学的价值。
教学重、难点:
教学重点:使学生理解并掌握3的倍数特征。
教学难点:发现并归纳3的倍数特征的过程。
个人资料:
年龄: 27岁 教龄:8 年
所任年级:5年级 人数:40人
男生:18人 女生:22人
电话号码:69720736
1)5的倍数的特征是:
个位上是0、5的数
2)2的倍数的特征是:
个位上是0、2、4、6、8的数
3×1 = 3
3×2 = 6
3×3 = 9
3×4 = 12
3×5 = 15
3×6 = 18
······
先把 3 的倍
数找出来。
1 + 2 = 3
1 + 5 = 6
······
3 的倍数的个位上的数是不是 3 的倍数呢
3,6,9 是 3 的倍数,但 12,15,18 个位上的数就不是 3 的倍数。
12 个位上的数不是 3 的倍数,
但 1 + 2 = 3, 3 是3 的倍数。
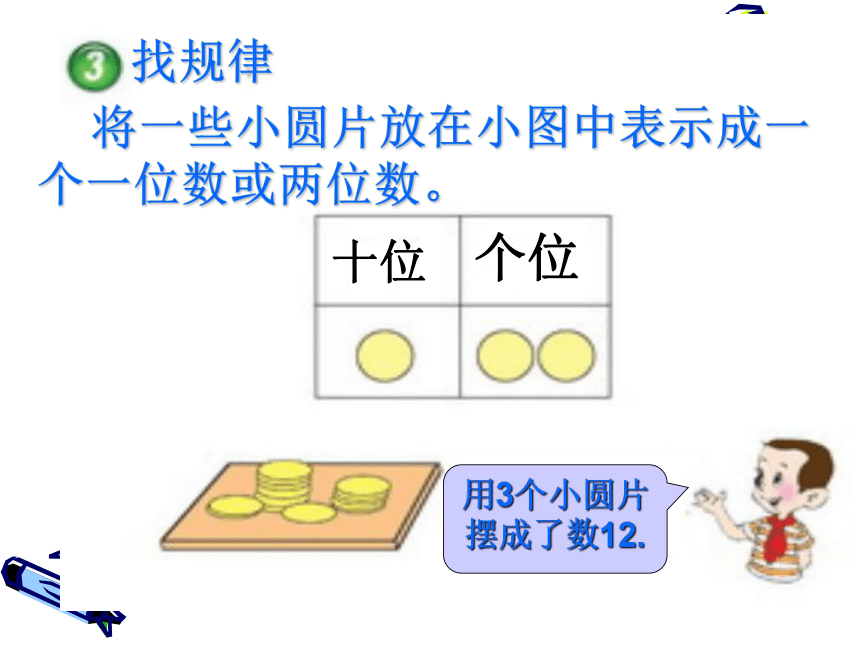
用3个小圆片摆成了数12.
找规律
将一些小圆片放在小图中表示成一个一位数或两位数。
十位
个位
同桌一人摆圆片,一人填表;
填好后想一想:
①组成的数与圆片个数有什么关系?
②圆片个数与3的倍数有什么关系?
合作要求:
圆片的个数(个) 3 5
组成的数 12 23 54 15
是不是3的倍数 是 不是
9
是
6
是
填表,判断所组成的数是不是的倍数。
想一想 观察上表,你发想了什么?
组成的这些数,各数位上的数字之和等于圆片个数。
当圆片个数是3的倍数时,所组成的数就是3的倍数。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3
试一试
在方格中把 的倍数做上记号。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3
3
在表中任取一个 的倍数,
把它个位上与十位上的数字
相加,和还是 的倍数吗?
试一试
3的倍数的特征:
一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。
【注意】:与2、5的倍数的特征不同,3的倍数的个位上可以是任何数字。
个人资料:
年龄: 27 岁 教龄:8 年
所任年级:5年级 人数:40人
男生:18人 女生:22人
电话号码:69720736
老师家的电话号码是63665269,它是3的倍数吗?
6+3+6+6+5+2+6+9=43
猜一猜:
4
3
+
=7
×
这种方法叫做“加、连加法”。
还有更快的方法吗?
老师家的电话号码是63665269,它是3的倍数吗?
猜一猜:
方法2: 6 3 6 6 5 2 6 9
5+2=7 , 所以63665269不是3的倍数 。
这种判断方法叫做弃3倍数法。
试一试
(1)4+2=6
1.判断下列数是不是3的倍数
42 134 78 268
6是3的倍数
所以42是3的倍数
(2)1+3+4=8
8不是3的倍数
所以134不是3的倍数
(3)7+8=15
15是3的倍数
所以78是3的倍数
(4)2+6+8=16
所以268不是3的倍数
16不是3的倍数
2、在下面的方框里填上一个数字,使这个数是3的倍数。
0
1
258
147
3
6
9
7
3 2 6 2 5 47
4
找出最小的数然后依次加3
3、既是2和5的倍数,又是3的倍数的最小三位数是多少?
1
考虑到最小,就填1。
考虑到2和5的倍数的特征,就填0。
0
考虑3的倍数的特征,十位上填什么?
2
谢谢大家!
3 的倍数的特征
五年级数学下册
教学目标:
1、通过观察,探索,验证等活动,让学生经历发现3的倍数特征的过程,培养学生自主探索,合作交流的良好习惯;
2、理解并掌握3的倍数特征,并能熟练的用3的倍数特征解决实际问题。
3、让学生在探索过程中感受数学的奥妙,在运用规律中体现数学的价值。
教学重、难点:
教学重点:使学生理解并掌握3的倍数特征。
教学难点:发现并归纳3的倍数特征的过程。
个人资料:
年龄: 27岁 教龄:8 年
所任年级:5年级 人数:40人
男生:18人 女生:22人
电话号码:69720736
1)5的倍数的特征是:
个位上是0、5的数
2)2的倍数的特征是:
个位上是0、2、4、6、8的数
3×1 = 3
3×2 = 6
3×3 = 9
3×4 = 12
3×5 = 15
3×6 = 18
······
先把 3 的倍
数找出来。
1 + 2 = 3
1 + 5 = 6
······
3 的倍数的个位上的数是不是 3 的倍数呢
3,6,9 是 3 的倍数,但 12,15,18 个位上的数就不是 3 的倍数。
12 个位上的数不是 3 的倍数,
但 1 + 2 = 3, 3 是3 的倍数。
用3个小圆片摆成了数12.
找规律
将一些小圆片放在小图中表示成一个一位数或两位数。
十位
个位
同桌一人摆圆片,一人填表;
填好后想一想:
①组成的数与圆片个数有什么关系?
②圆片个数与3的倍数有什么关系?
合作要求:
圆片的个数(个) 3 5
组成的数 12 23 54 15
是不是3的倍数 是 不是
9
是
6
是
填表,判断所组成的数是不是的倍数。
想一想 观察上表,你发想了什么?
组成的这些数,各数位上的数字之和等于圆片个数。
当圆片个数是3的倍数时,所组成的数就是3的倍数。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3
试一试
在方格中把 的倍数做上记号。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3
3
在表中任取一个 的倍数,
把它个位上与十位上的数字
相加,和还是 的倍数吗?
试一试
3的倍数的特征:
一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。
【注意】:与2、5的倍数的特征不同,3的倍数的个位上可以是任何数字。
个人资料:
年龄: 27 岁 教龄:8 年
所任年级:5年级 人数:40人
男生:18人 女生:22人
电话号码:69720736
老师家的电话号码是63665269,它是3的倍数吗?
6+3+6+6+5+2+6+9=43
猜一猜:
4
3
+
=7
×
这种方法叫做“加、连加法”。
还有更快的方法吗?
老师家的电话号码是63665269,它是3的倍数吗?
猜一猜:
方法2: 6 3 6 6 5 2 6 9
5+2=7 , 所以63665269不是3的倍数 。
这种判断方法叫做弃3倍数法。
试一试
(1)4+2=6
1.判断下列数是不是3的倍数
42 134 78 268
6是3的倍数
所以42是3的倍数
(2)1+3+4=8
8不是3的倍数
所以134不是3的倍数
(3)7+8=15
15是3的倍数
所以78是3的倍数
(4)2+6+8=16
所以268不是3的倍数
16不是3的倍数
2、在下面的方框里填上一个数字,使这个数是3的倍数。
0
1
258
147
3
6
9
7
3 2 6 2 5 47
4
找出最小的数然后依次加3
3、既是2和5的倍数,又是3的倍数的最小三位数是多少?
1
考虑到最小,就填1。
考虑到2和5的倍数的特征,就填0。
0
考虑3的倍数的特征,十位上填什么?
2
谢谢大家!
