第十八章 平行四边形 单元检测卷(学生版+教师版)
文档属性
| 名称 | 第十八章 平行四边形 单元检测卷(学生版+教师版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 20:09:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八下第十八章 平行四边形 单元检测卷(学生版)
一、选择题(每小题3分,共30分)
1.在ABCD中,AB=3,AD=5,则ABCD的周长等于( )
A.6 B.8 C.10 D.16
2.在ABCD中,∠A+∠C=100°,则∠B的大小为( )
A.50° B.80° C.130° D.150°
3.四边形ABCD是矩形,则不一定成立的是( )
A.AD=BC B.∠C=90° C.AC=BD D.AC⊥BD
4.四边形ABCD是菱形,AC=6,BC=8,则四边形ABCD的面积为( )
A.24 B.28 C.30 D.48
5.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
6.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD,则四边形ABCD是( )
A.一般平行四边形 B.矩形 C.菱形 D.正方形
7.如图,直线l上有三个正方形①、②和③,若①和②的面积分别为2和6,则③的边长为( )
A.2 B.2 C.4 D.4
8.如图,在ABCD中,O为对角线的交点,E为BC边的中点,AB=6,AD=8,BD=12,则△BOE的周长为( )
A.11 B.12 C.13 D.14
9.如图,在矩形ABCD中,O为对角线的交点,AE⊥BD于点E,BE=8,DE=18,则四边形ABCD的面积为( )
A.156 B.228 C.306 D.312
10.在平面直角坐标系中,四边形ABCD是平行四边形,点A(1,4)、B(a,a)、C(3,2)则对角线BD的长最小值为( )
A.10 B.2 C.5 D.2
二、填空题(每小题3分,共18分)
11.在△ABC中,点D、E分别AB和AC的中点,则DE与BC的位置关系为____________(填“平行”或“垂直”)
12.已知ABCD,对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个菱形,你添加的条件是______________
13.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角的度数为________
14.如图:△AEF的顶点E、F分别在正方形ABCD的边BC和CD上,BE=2,CE=1,∠EAF=45°,则DF的长为____________
15.ABCD内一点P到边AB、BC、CD和AD的距离分别是1,2,3,4,则ABCD面积的最小值为____________
16.如图,在ABCD中,对角线AC与BD交于点O,AB=10,BD=2,∠BAC=2∠CAD,则ABCD的面积为______________
三、解答题(共8小题,72分)
17.(本小题8分)如图,ABCD和AECF的顶点B,E,F,D在同一条直线上,求证:BE=DF.
18.(本小题8分)如图,四边形ABCD是菱形,点E、F、G和H分别是其边AB、BC、CD和AD的中点,求证:四边形EFGH是矩形.
19.(本小题8分)如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
(1)求证:四边形ADEF是平行四边形
(2)当△ABC满足什么条件时,四边形ADEF正方形(不用说明理由).
20.(本小题8分)如图,在正方形ABCD中,点E为对角线BD上一点, EF⊥AE交BC于点F.
(1)求证:AE=EF;
(2)若DE=1,请直接写出CF的长.
21.(本小题8分)如图,平面直角坐标系中,已知点A(2,6)、B(5,2)
(1)若存在C(m,0)、D(0,n),使以A、B、C、D四个点为顶点的四边形是平行四边形,求m和n的值;
(2)若存在C(0,m),D,使四边形ABCD是菱形,请直接写出m的值。
22.(本小题10分)如图,在△ABC中,点D、E分别是边AC和AB的中点,BD交CE于点O.
(1)求证:OB=2OD;
(2)若BD⊥CE,∠CBD=30°,BC=4,求AC的长.
23.(本小题10分)如图1,在△ABC中,AB=AC=4,AB⊥AC,D为BC的中点,E、F分别为边AB、AC上一动点,且∠EDF=90°.
(1)求证:△DEF是等腰直角三角形;
(2)如图2,G为线段EF中点,连接并延长AG交BC于点H,连接EH、FH,请判断四边形AEHF的形状,并给出证明:
(3)在(2)的条件下,若点E从B点出发沿BA方向运动到使△AEF的面积最大时停止,则在此过程中点G运动的路径长为_____________
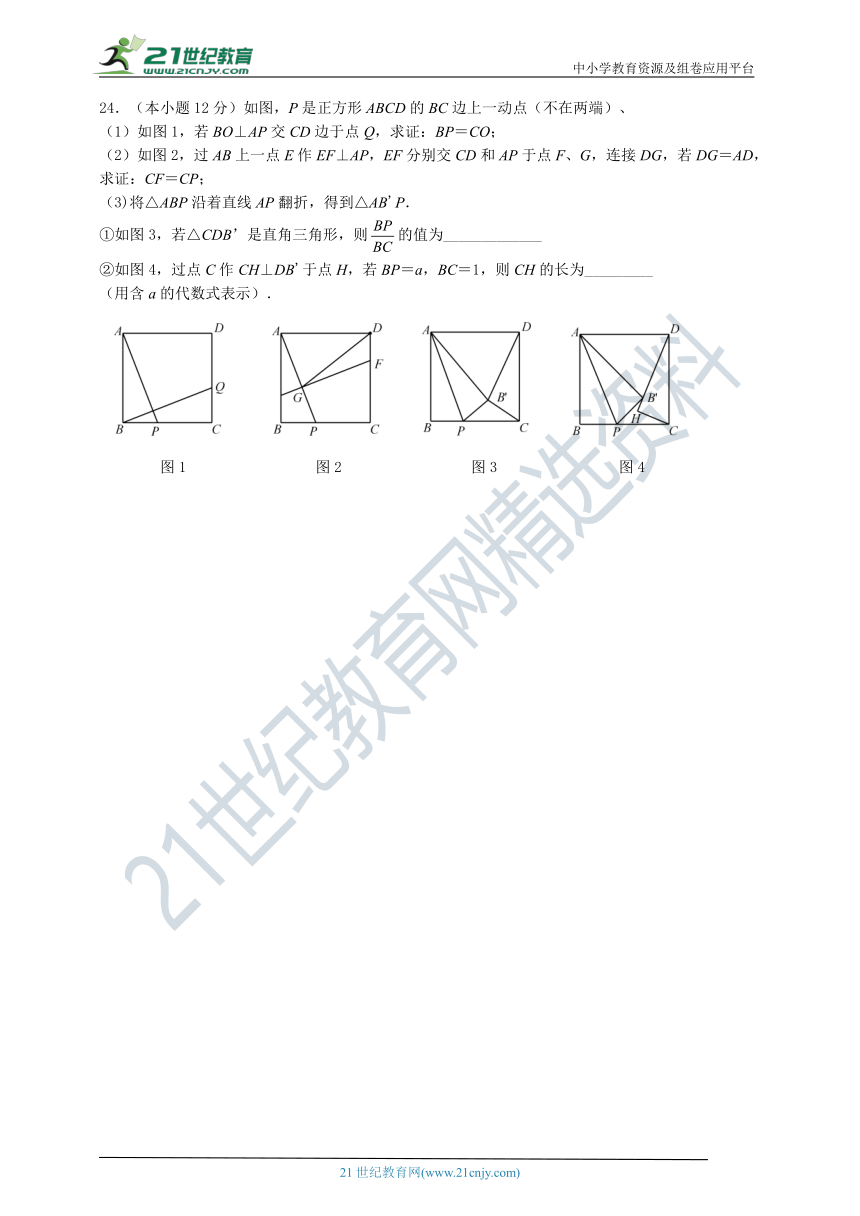
24.(本小题12分)如图,P是正方形ABCD的BC边上一动点(不在两端)、
(1)如图1,若BO⊥AP交CD边于点Q,求证:BP=CO;
(2)如图2,过AB上一点E作EF⊥AP,EF分别交CD和AP于点F、G,连接DG,若DG=AD,求证:CF=CP;
(3)将△ABP沿着直线AP翻折,得到△AB'P.
①如图3,若△CDB’是直角三角形,则的值为_____________
②如图4,过点C作CH⊥DB'于点H,若BP=a,BC=1,则CH的长为_________
(用含a的代数式表示).
图1 图2 图3 图4
八下 第十八章 平行四边形单元检测卷(教师版)
一、选择题(每小题3分,共30分)
1.在ABCD中,AB=3,AD=5,则ABCD的周长等于( )
A.6 B.8 C.10 D.16
答案:D
2.在ABCD中,∠A+∠C=100°,则∠B的大小为( )
A.50° B.80° C.130° D.150°
答案:C
3.四边形ABCD是矩形,则不一定成立的是( )
A.AD=BC B.∠C=90° C.AC=BD D.AC⊥BD
答案:D
4.四边形ABCD是菱形,AC=6,BC=8,则四边形ABCD的面积为( )
A.24 B.28 C.30 D.48
答案:A
5.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
答案:C
6.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD,则四边形ABCD是( )
答案:C
A.一般平行四边形 B.矩形 C.菱形 D.正方形
7.如图,直线l上有三个正方形①、②和③,若①和②的面积分别为2和6,则③的边长为( )
A.2 B.2 C.4 D.4
答案:B
8.如图,在ABCD中,O为对角线的交点,E为BC边的中点,AB=6,AD=8,BD=12,则△BOE的周长为( )
A.11 B.12 C.13 D.14
答案:C
9.如图,在矩形ABCD中,O为对角线的交点,AE⊥BD于点E,BE=8,DE=18,则四边形ABCD的面积为( )
A.156 B.228 C.306 D.312
答案:D
10.在平面直角坐标系中,四边形ABCD是平行四边形,点A(1,4)、B(a,a)、C(3,2)则对角线BD的长最小值为( )
A.10 B.2 C.5 D.2
答案:C
解析:考虑A、C的中点(2,3)到第二、四象限角平分线的距离即可
二、填空题(每小题3分,共18分)
11.在△ABC中,点D、E分别AB和AC的中点,则DE与BC的位置关系为____________(填“平行”或“垂直”)
答案:DE∥BC
12.已知ABCD,对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个菱形,你添加的条件是______________
答案:AB=BC(答案不唯一)
13.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角的度数为________
答案:80
14.如图:△AEF的顶点E、F分别在正方形ABCD的边BC和CD上,BE=2,CE=1,∠EAF=45°,则DF的长为____________
答案:
15.ABCD内一点P到边AB、BC、CD和AD的距离分别是1,2,3,4,则ABCD面积的最小值为____________
答案:24
16.如图,在ABCD中,对角线AC与BD交于点O,AB=10,BD=2,∠BAC=2∠CAD,则ABCD的面积为______________
答案:156
解析:在线段AC上取点E,使AE=DE,过点D作DFLAC于点F,则AE=DE=CD=AB=10,F为CE的中点,O为AC的中点,易知OF=AE=5,在Rt三角形ODF中,根据勾股定理得DF=6
三、解答题(共8小题,72分)
17.(本小题8分)如图,ABCD和AECF的顶点B,E,F,D在同一条直线上,求证:BE=DF.
答案:连接AC
18.(本小题8分)如图,四边形ABCD是菱形,点E、F、G和H分别是其边AB、BC、CD和AD的中点,求证:四边形EFGH是矩形.
答案:连接AC、BD
19.(本小题8分)如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
(1)求证:四边形ADEF是平行四边形
(2)当△ABC满足什么条件时,四边形ADEF正方形(不用说明理由).
答案:(1)略;(2)AB=AC且∠BAC=150°
20.(本小题8分)如图,在正方形ABCD中,点E为对角线BD上一点, EF⊥AE交BC于点F.
(1)求证:AE=EF;
(2)若DE=1,请直接写出CF的长.
答案:(1)略;(2)CF=
21.(本小题8分)如图,平面直角坐标系中,已知点A(2,6)、B(5,2)
(1)若存在C(m,0)、D(0,n),使以A、B、C、D四个点为顶点的四边形是平行四边形,求m和n的值;
(2)若存在C(0,m),D,使四边形ABCD是菱形,请直接写出m的值。
答案:(1)或或;(2)m=
22.(本小题10分)如图,在△ABC中,点D、E分别是边AC和AB的中点,BD交CE于点O.
(1)求证:OB=2OD;
(2)若BD⊥CE,∠CBD=30°,BC=4,求AC的长.
答案:
(1)提示:分别取OB和OC的中点P和Q,证四边形EPQD是平行四边形;
(2)2
23.(本小题10分)如图1,在△ABC中,AB=AC=4,AB⊥AC,D为BC的中点,E、F分别为边AB、AC上一动点,且∠EDF=90°.
(1)求证:△DEF是等腰直角三角形;
(2)如图2,G为线段EF中点,连接并延长AG交BC于点H,连接EH、FH,请判断四边形AEHF的形状,并给出证明:
(3)在(2)的条件下,若点E从B点出发沿BA方向运动到使△AEF的面积最大时停止,则在此过程中点G运动的路径长为_____________
答案:
(1)提示:连接AD,证△BDE≌△ADF;
(2)矩形(提示:连接DG,则易证GH=DG=AG);
(3)(提示:取AB中点P,连接PG,则PG∥BH且PG=BH,∴点G的运动路径长度是点H运动路径长度的一半;另外,当E在AB中点时,△AEF的面积最大.)
24.(本小题12分)如图,P是正方形ABCD的BC边上一动点(不在两端)、
(1)如图1,若BO⊥AP交CD边于点Q,求证:BP=CO;
(2)如图2,过AB上一点E作EF⊥AP,EF分别交CD和AP于点F、G,连接DG,若DG=AD,求证:CF=CP;
(3)将△ABP沿着直线AP翻折,得到△AB'P.
①如图3,若△CDB’是直角三角形,则的值为_____________
②如图4,过点C作CH⊥DB'于点H,若BP=a,BC=1,则CH的长为_________
(用含a的代数式表示).
图1 图2 图3 图4
答案:
(1)略;(2)提示:过D作DQ⊥AP交AB于点Q,连QG,证DF=EQ=BP,AQ=QG=EQ;
(3)①(提示:延长PB’交CD手点M,连AM,证MC=MD,∠PAM=45°,
设DM=CM=t,BP=x,证PM=BP+DM,在Rt△PCM中应用勾股定理);
②
(思路同①,另外CH=DB’)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八下第十八章 平行四边形 单元检测卷(学生版)
一、选择题(每小题3分,共30分)
1.在ABCD中,AB=3,AD=5,则ABCD的周长等于( )
A.6 B.8 C.10 D.16
2.在ABCD中,∠A+∠C=100°,则∠B的大小为( )
A.50° B.80° C.130° D.150°
3.四边形ABCD是矩形,则不一定成立的是( )
A.AD=BC B.∠C=90° C.AC=BD D.AC⊥BD
4.四边形ABCD是菱形,AC=6,BC=8,则四边形ABCD的面积为( )
A.24 B.28 C.30 D.48
5.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
6.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD,则四边形ABCD是( )
A.一般平行四边形 B.矩形 C.菱形 D.正方形
7.如图,直线l上有三个正方形①、②和③,若①和②的面积分别为2和6,则③的边长为( )
A.2 B.2 C.4 D.4
8.如图,在ABCD中,O为对角线的交点,E为BC边的中点,AB=6,AD=8,BD=12,则△BOE的周长为( )
A.11 B.12 C.13 D.14
9.如图,在矩形ABCD中,O为对角线的交点,AE⊥BD于点E,BE=8,DE=18,则四边形ABCD的面积为( )
A.156 B.228 C.306 D.312
10.在平面直角坐标系中,四边形ABCD是平行四边形,点A(1,4)、B(a,a)、C(3,2)则对角线BD的长最小值为( )
A.10 B.2 C.5 D.2
二、填空题(每小题3分,共18分)
11.在△ABC中,点D、E分别AB和AC的中点,则DE与BC的位置关系为____________(填“平行”或“垂直”)
12.已知ABCD,对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个菱形,你添加的条件是______________
13.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角的度数为________
14.如图:△AEF的顶点E、F分别在正方形ABCD的边BC和CD上,BE=2,CE=1,∠EAF=45°,则DF的长为____________
15.ABCD内一点P到边AB、BC、CD和AD的距离分别是1,2,3,4,则ABCD面积的最小值为____________
16.如图,在ABCD中,对角线AC与BD交于点O,AB=10,BD=2,∠BAC=2∠CAD,则ABCD的面积为______________
三、解答题(共8小题,72分)
17.(本小题8分)如图,ABCD和AECF的顶点B,E,F,D在同一条直线上,求证:BE=DF.
18.(本小题8分)如图,四边形ABCD是菱形,点E、F、G和H分别是其边AB、BC、CD和AD的中点,求证:四边形EFGH是矩形.
19.(本小题8分)如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
(1)求证:四边形ADEF是平行四边形
(2)当△ABC满足什么条件时,四边形ADEF正方形(不用说明理由).
20.(本小题8分)如图,在正方形ABCD中,点E为对角线BD上一点, EF⊥AE交BC于点F.
(1)求证:AE=EF;
(2)若DE=1,请直接写出CF的长.
21.(本小题8分)如图,平面直角坐标系中,已知点A(2,6)、B(5,2)
(1)若存在C(m,0)、D(0,n),使以A、B、C、D四个点为顶点的四边形是平行四边形,求m和n的值;
(2)若存在C(0,m),D,使四边形ABCD是菱形,请直接写出m的值。
22.(本小题10分)如图,在△ABC中,点D、E分别是边AC和AB的中点,BD交CE于点O.
(1)求证:OB=2OD;
(2)若BD⊥CE,∠CBD=30°,BC=4,求AC的长.
23.(本小题10分)如图1,在△ABC中,AB=AC=4,AB⊥AC,D为BC的中点,E、F分别为边AB、AC上一动点,且∠EDF=90°.
(1)求证:△DEF是等腰直角三角形;
(2)如图2,G为线段EF中点,连接并延长AG交BC于点H,连接EH、FH,请判断四边形AEHF的形状,并给出证明:
(3)在(2)的条件下,若点E从B点出发沿BA方向运动到使△AEF的面积最大时停止,则在此过程中点G运动的路径长为_____________
24.(本小题12分)如图,P是正方形ABCD的BC边上一动点(不在两端)、
(1)如图1,若BO⊥AP交CD边于点Q,求证:BP=CO;
(2)如图2,过AB上一点E作EF⊥AP,EF分别交CD和AP于点F、G,连接DG,若DG=AD,求证:CF=CP;
(3)将△ABP沿着直线AP翻折,得到△AB'P.
①如图3,若△CDB’是直角三角形,则的值为_____________
②如图4,过点C作CH⊥DB'于点H,若BP=a,BC=1,则CH的长为_________
(用含a的代数式表示).
图1 图2 图3 图4
八下 第十八章 平行四边形单元检测卷(教师版)
一、选择题(每小题3分,共30分)
1.在ABCD中,AB=3,AD=5,则ABCD的周长等于( )
A.6 B.8 C.10 D.16
答案:D
2.在ABCD中,∠A+∠C=100°,则∠B的大小为( )
A.50° B.80° C.130° D.150°
答案:C
3.四边形ABCD是矩形,则不一定成立的是( )
A.AD=BC B.∠C=90° C.AC=BD D.AC⊥BD
答案:D
4.四边形ABCD是菱形,AC=6,BC=8,则四边形ABCD的面积为( )
A.24 B.28 C.30 D.48
答案:A
5.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.∠A=∠C D.∠A=∠B
答案:C
6.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD,则四边形ABCD是( )
答案:C
A.一般平行四边形 B.矩形 C.菱形 D.正方形
7.如图,直线l上有三个正方形①、②和③,若①和②的面积分别为2和6,则③的边长为( )
A.2 B.2 C.4 D.4
答案:B
8.如图,在ABCD中,O为对角线的交点,E为BC边的中点,AB=6,AD=8,BD=12,则△BOE的周长为( )
A.11 B.12 C.13 D.14
答案:C
9.如图,在矩形ABCD中,O为对角线的交点,AE⊥BD于点E,BE=8,DE=18,则四边形ABCD的面积为( )
A.156 B.228 C.306 D.312
答案:D
10.在平面直角坐标系中,四边形ABCD是平行四边形,点A(1,4)、B(a,a)、C(3,2)则对角线BD的长最小值为( )
A.10 B.2 C.5 D.2
答案:C
解析:考虑A、C的中点(2,3)到第二、四象限角平分线的距离即可
二、填空题(每小题3分,共18分)
11.在△ABC中,点D、E分别AB和AC的中点,则DE与BC的位置关系为____________(填“平行”或“垂直”)
答案:DE∥BC
12.已知ABCD,对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个菱形,你添加的条件是______________
答案:AB=BC(答案不唯一)
13.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角的度数为________
答案:80
14.如图:△AEF的顶点E、F分别在正方形ABCD的边BC和CD上,BE=2,CE=1,∠EAF=45°,则DF的长为____________
答案:
15.ABCD内一点P到边AB、BC、CD和AD的距离分别是1,2,3,4,则ABCD面积的最小值为____________
答案:24
16.如图,在ABCD中,对角线AC与BD交于点O,AB=10,BD=2,∠BAC=2∠CAD,则ABCD的面积为______________
答案:156
解析:在线段AC上取点E,使AE=DE,过点D作DFLAC于点F,则AE=DE=CD=AB=10,F为CE的中点,O为AC的中点,易知OF=AE=5,在Rt三角形ODF中,根据勾股定理得DF=6
三、解答题(共8小题,72分)
17.(本小题8分)如图,ABCD和AECF的顶点B,E,F,D在同一条直线上,求证:BE=DF.
答案:连接AC
18.(本小题8分)如图,四边形ABCD是菱形,点E、F、G和H分别是其边AB、BC、CD和AD的中点,求证:四边形EFGH是矩形.
答案:连接AC、BD
19.(本小题8分)如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
(1)求证:四边形ADEF是平行四边形
(2)当△ABC满足什么条件时,四边形ADEF正方形(不用说明理由).
答案:(1)略;(2)AB=AC且∠BAC=150°
20.(本小题8分)如图,在正方形ABCD中,点E为对角线BD上一点, EF⊥AE交BC于点F.
(1)求证:AE=EF;
(2)若DE=1,请直接写出CF的长.
答案:(1)略;(2)CF=
21.(本小题8分)如图,平面直角坐标系中,已知点A(2,6)、B(5,2)
(1)若存在C(m,0)、D(0,n),使以A、B、C、D四个点为顶点的四边形是平行四边形,求m和n的值;
(2)若存在C(0,m),D,使四边形ABCD是菱形,请直接写出m的值。
答案:(1)或或;(2)m=
22.(本小题10分)如图,在△ABC中,点D、E分别是边AC和AB的中点,BD交CE于点O.
(1)求证:OB=2OD;
(2)若BD⊥CE,∠CBD=30°,BC=4,求AC的长.
答案:
(1)提示:分别取OB和OC的中点P和Q,证四边形EPQD是平行四边形;
(2)2
23.(本小题10分)如图1,在△ABC中,AB=AC=4,AB⊥AC,D为BC的中点,E、F分别为边AB、AC上一动点,且∠EDF=90°.
(1)求证:△DEF是等腰直角三角形;
(2)如图2,G为线段EF中点,连接并延长AG交BC于点H,连接EH、FH,请判断四边形AEHF的形状,并给出证明:
(3)在(2)的条件下,若点E从B点出发沿BA方向运动到使△AEF的面积最大时停止,则在此过程中点G运动的路径长为_____________
答案:
(1)提示:连接AD,证△BDE≌△ADF;
(2)矩形(提示:连接DG,则易证GH=DG=AG);
(3)(提示:取AB中点P,连接PG,则PG∥BH且PG=BH,∴点G的运动路径长度是点H运动路径长度的一半;另外,当E在AB中点时,△AEF的面积最大.)
24.(本小题12分)如图,P是正方形ABCD的BC边上一动点(不在两端)、
(1)如图1,若BO⊥AP交CD边于点Q,求证:BP=CO;
(2)如图2,过AB上一点E作EF⊥AP,EF分别交CD和AP于点F、G,连接DG,若DG=AD,求证:CF=CP;
(3)将△ABP沿着直线AP翻折,得到△AB'P.
①如图3,若△CDB’是直角三角形,则的值为_____________
②如图4,过点C作CH⊥DB'于点H,若BP=a,BC=1,则CH的长为_________
(用含a的代数式表示).
图1 图2 图3 图4
答案:
(1)略;(2)提示:过D作DQ⊥AP交AB于点Q,连QG,证DF=EQ=BP,AQ=QG=EQ;
(3)①(提示:延长PB’交CD手点M,连AM,证MC=MD,∠PAM=45°,
设DM=CM=t,BP=x,证PM=BP+DM,在Rt△PCM中应用勾股定理);
②
(思路同①,另外CH=DB’)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
