2021-2022学年苏科版七年级数学下册第9章整式乘法与因式分解 单元达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册第9章整式乘法与因式分解 单元达标测试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 135.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 20:37:37 | ||
图片预览




文档简介
2021-2022学年苏科版七年级数学下册《第9章整式乘法与因式分解》
单元达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下面运算中正确的是( )
A.m2 m3=m6 B.m2+m2=2m4
C.(﹣3a2b)2=6a4b2 D.(﹣2x2) (﹣5x4)=10x6
2.下列各式由左边到右边的变形中,是因式分解的为( )
A.a(x+y)=ax+ay
B.10x2﹣5x=5x(2x﹣1)
C.x2﹣4x+4=(x﹣4)2
D.x2﹣16+3x=(x+4)(x﹣4)+3x
3.如果x2+2x=3,那么x4+7x3+8x2﹣13x+15的值为( )
A.16 B.18 C.0 D.无法确定
4.计算(﹣2)2021+(﹣2)2020的值是( )
A.﹣2 B.﹣22020 C.22020 D.2
5.已知:a=2020x+2019,b=2020x+2020,c=2020x+2021,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0 B.1 C.2 D.3
6.下列多项式能用平方差公式分解的因式有( )
(1)a2+b2;(2)x2﹣y2;(3)﹣m2+n2;(4)﹣b2﹣a2;(5)﹣a6+4.
A.2个 B.3个 C.4个 D.5个
7.观察:(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,据此规律,当(x﹣1)(x5+x4+x3+x2+x+1)=0时,代数式x2021﹣1的值为( )
A.1 B.0 C.1或﹣1 D.0或﹣2
8.已知m2=2﹣n,n2=m+2(m+n≠0),则m3+2mn﹣n3=( )
A.0 B.1 C.2 D.﹣2
二.填空题(共8小题,满分40分)
9.已知x2+mx+16能用完全平方公式因式分解,则m的值为 .
10.因式分解:12x2y3﹣8x3y2+20x2y2= .
11.已知xy=﹣1,x+y=2,则x3y+2x2y2+xy3= .
12.化简:(a+2)(a2+4)(a4+16)(a﹣2)= .
13.多项式x2﹣8x+m=(x﹣9)(x﹣n),则m+n= .
14.若关于x的多项式(x+m)(2x﹣3)展开后不含x项,则m的值为 .
15.若(2022﹣a)(2021﹣a)=2020,则(2022﹣a)2+(2021﹣a)2= .
16.如图,小颖用4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若a=2b,则S1、S2之间存在的数量关系是 .
三.解答题(共5小题,满分40分)
17.计算:
(1)(x+2)(4x﹣2).
(2)(a+2b)(a2﹣4b2)(a﹣2b).
18.计算:(2x﹣3y)(3x+2y)﹣(2x﹣3y)2.
19.已知(x+y)2=7,(x﹣y)2=5.
(1)求x2+y2值;
(2)求xy的值.
20.因式分解:
(1)m3n﹣6m2n+9mn;
(2)4x2﹣(x2+1)2;
(3)利用因式分解计算:(﹣2)2022+(﹣2)2021﹣22020.
21.先化简,再求值:[(x﹣3y)2﹣(x﹣y)(x+y)+4xy]÷2y,其中x=﹣2,y=1.
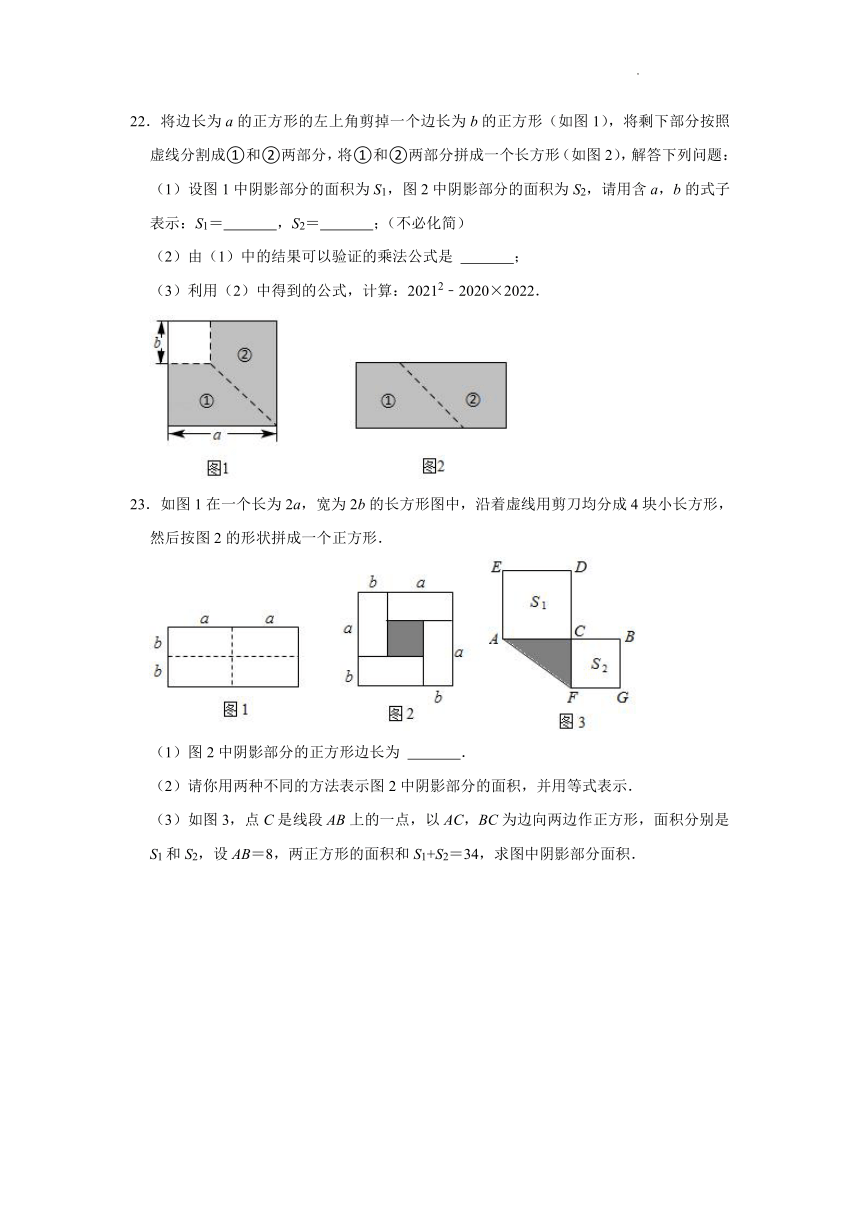
22.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2),解答下列问题:
(1)设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2,请用含a,b的式子表示:S1= ,S2= ;(不必化简)
(2)由(1)中的结果可以验证的乘法公式是 ;
(3)利用(2)中得到的公式,计算:20212﹣2020×2022.
23.如图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分面积.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、m2 m3=m5,本选项计算错误,不符合题意;
B、m2+m2=2m2,本选项计算错误,不符合题意;
C、(﹣3a2b)2=9a4b2,本选项计算错误,不符合题意;
D、(﹣2x2) (﹣5x4)=10x6,本选项计算正确,符合题意;
故选:D.
2.解:A选项,等号右边不是积的形式,故该选项不符合题意;
B选项,10x2﹣5x=5x(2x﹣1),故该选项符合题意;
C选项,等号右边=x2﹣8x+16≠左边,故该选项不符合题意;
D选项,等号右边不是积的形式,故该选项不符合题意;
故选:B.
3.解:∵x +2x=3.
∴x (x +2x)=3x .
∴x4+2x =3x .
∴原式=x4+2x +5x +8x ﹣13x+15
=5x +3x +8x ﹣13x+15
=5x +10x +x ﹣13x+15
=5x(x +2x)+x ﹣13x+15
=5x×3+x ﹣13x+15
=x +2x+15
=3+15
=18.
故选:B.
4.解:(﹣2)2021+(﹣2)2020
=(﹣2)2020×(﹣2+1)
=﹣22020.
故选:B.
5.解:∵a=2020x+2019,b=2020x+2020,c=2020x+2021,
∴a﹣b=﹣1,a﹣c=﹣2,b﹣c=﹣1.
设S=a2+b2+c2﹣ab﹣ac﹣bc,
则2S=2a2+2b2+2c2﹣2ab﹣2ac﹣2bc.
∵2a2+2b2+2c2﹣2ab﹣2ac﹣2bc
=a2﹣2ab+b2+a2﹣2ac+c2+b2﹣2bc+c2
=(a﹣b)2+(a﹣c)2+(b﹣c)2
=(﹣1)2+(﹣2)2+(﹣1)2
=6,
∴S=3.
∴a2+b2+c2﹣ab﹣ac﹣bc=3.
故选:D.
6.解:(1)a2+b2,不符合题意;
(2)x2﹣y2=(x+y)(x﹣y),符合题意;
(3)﹣m2+n2
=n2﹣m2
=(n+m)(n﹣m),符合题意;
(4)﹣b2﹣a2=﹣(b2+a2),不符合题意;
(5)﹣a6+4.
=4﹣a6
=(4+a3)(4﹣a3),符合题意;
故选:B.
7.解:∵(x﹣1)(x5+x4+x3+x2+x+1)=0.
∴x6﹣1=0.
∴x6=1.
∴(x3)2=1.
∴x3=±1.
∴x=±1.
当x=1时,原式=12021﹣1=0.
当x=﹣1时,原式=12021﹣1=﹣2.
故选:D.
8.解:∵m2=2﹣n,n2=m+2,
∴m2﹣n2=(m+n)(m﹣n)=2﹣n﹣m﹣2=﹣(m+n),
∴m﹣n=﹣1,
∵m3=m m2=m(2﹣n)=2m﹣mn,n3=n n2=n(m+2)=mn+2n,
∴m3+2mn﹣n3=2m﹣mn+2mn﹣mn﹣2n=2(m﹣n)=﹣2,
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵x2+mx+16能用完全平方公式进行因式分解,x2+mx+16=x2+mx+42,
∴m=2×4=8或m=﹣(2×4)=﹣8,
∴m的值为±8.
故答案为:±8.
10.解:原式=4x2y2 3y﹣4x2y2 2x+4x2y2 5
=4x2y2(3y﹣2x+5).
故答案为:4x2y2(3y﹣2x+5).
11.解:∵xy=﹣1,x+y=2,
∴x3y+2x2y2+xy3
=xy(x2+2xy+y2)
=xy(x+y)2
=﹣1×22
=﹣4.
故答案为:﹣4.
12.解:(a+2)(a2+4)(a4+16)(a﹣2)
=(a+2)(a﹣2)(a2+4)(a4+16)
=(a2﹣4)(a2+4)(a4+16)
=(a4﹣16)(a4+16)
=a8﹣256.
故答案为:a8﹣256.
13.解:∵多项式x2﹣8x+m=(x﹣9)(x﹣n),
∴x2﹣8x+m=x +(﹣n﹣9)x+9n.
∴﹣n﹣9=﹣8,m=9n.
∴m=﹣9,n=﹣1.
∴m+n=﹣9+(﹣1)=﹣10.
故答案为:﹣10.
14.解:原式=2x2+(2m﹣3)x﹣3m,
∵多项式展开后不含x项,
∴2m﹣3=0,
∴m=;
故答案为:.
15.解:设x=2022﹣a,y=2021﹣a,
∴xy=2020,x﹣y=2022﹣a﹣2021+a=1,
∴(2022﹣a)2+(2021﹣a)2
=x2+y2
=(x﹣y)2+2xy
=1+2×2020
=4041.
故答案为:4041.
16.解:S1=b(a+b)×2+ab×2+(a﹣b)2=a2+2b2,
S2=(a+b)2﹣S1=(a+b)2﹣(a2+2b2)=2ab﹣b2,
∵a=2b,
∴S1=a2+2b2=6b2,S2=2ab﹣b2=3b2
∴S1=2S2.
故答案为:S1=2S2.
三.解答题(共7小题,满分40分)
17.解:(1)原式=4x2﹣2x+8x﹣4
=4x2+6x﹣4;
(2)原式=(a+2b)(a﹣2b)(a2﹣4b2)
=(a2﹣4b2)2
=a4﹣8a2b2+16b4.
.
18.解:原式=6x +4xy﹣9xy﹣6y ﹣(4x ﹣12xy+9y ).
=6x ﹣5xy﹣6y ﹣4x +12xy﹣9y .
=2x +7xy﹣15y .
19.解:(1)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①+②得:
x2+2xy+y2+x2﹣2xy+y2=12,
则x2+y2=6;
(2)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①﹣②得:
4xy=2,
解得:xy=
20.(1)m3n﹣6m2n+9mn=mn(m2﹣6m+9)=mn(m﹣3)2.
(2)4x2﹣(x2+1)2=(2x)2﹣(x2+1)2=(2x+x2+1)(2x﹣x2﹣1)=﹣(x2+2x+1)(x2﹣2x+1)
=﹣(x+1)2(x﹣1)2.
(3)原式=22022﹣22021﹣22020=22020(22﹣2﹣1)=22020.
21.解:原式=[x2﹣6xy+9y2﹣(x2﹣y2)+4xy]÷2y
=(x2﹣6xy+9y2﹣x2+y2+4xy)÷2y
=(﹣2xy+10y2)÷2y
=﹣x+5y,
当x=﹣2,y=1时,
原式=﹣(﹣2)+5×1
=2+5
=7.
22.解:(1)由题意得,S1=a2﹣b2,S2=(a+b)(a﹣b),
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由(1)中的结果可验证的乘法公式为(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b)=a2﹣b2;
(3)由(2)中所得乘法公式(a+b)(a﹣b)=a2﹣b2可得,
20212﹣2020×2022=20212﹣(2021+1)(2021﹣1)=20212﹣(20212﹣1)
=20212﹣20212+1
=1.
23.解:(1)由题意得:图2中阴影部分的正方形边长为:a﹣b.
故答案为:a﹣b.
(2)图2中阴影部分面积为:(a﹣b)2,还可以表示为:(a+b)2﹣4ab.
∴(a﹣b)2=(a+b)2﹣4ab.
(3)设AC=x,BC=y,由题意得:x+y=8,x2+y2=S1+S2=34.
∵(x+y)2=x2+y2+2xy.
∴64=34+2xy.
∴xy=15.
∴S阴影=AC CF=xy=7.5.
单元达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.下面运算中正确的是( )
A.m2 m3=m6 B.m2+m2=2m4
C.(﹣3a2b)2=6a4b2 D.(﹣2x2) (﹣5x4)=10x6
2.下列各式由左边到右边的变形中,是因式分解的为( )
A.a(x+y)=ax+ay
B.10x2﹣5x=5x(2x﹣1)
C.x2﹣4x+4=(x﹣4)2
D.x2﹣16+3x=(x+4)(x﹣4)+3x
3.如果x2+2x=3,那么x4+7x3+8x2﹣13x+15的值为( )
A.16 B.18 C.0 D.无法确定
4.计算(﹣2)2021+(﹣2)2020的值是( )
A.﹣2 B.﹣22020 C.22020 D.2
5.已知:a=2020x+2019,b=2020x+2020,c=2020x+2021,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0 B.1 C.2 D.3
6.下列多项式能用平方差公式分解的因式有( )
(1)a2+b2;(2)x2﹣y2;(3)﹣m2+n2;(4)﹣b2﹣a2;(5)﹣a6+4.
A.2个 B.3个 C.4个 D.5个
7.观察:(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,据此规律,当(x﹣1)(x5+x4+x3+x2+x+1)=0时,代数式x2021﹣1的值为( )
A.1 B.0 C.1或﹣1 D.0或﹣2
8.已知m2=2﹣n,n2=m+2(m+n≠0),则m3+2mn﹣n3=( )
A.0 B.1 C.2 D.﹣2
二.填空题(共8小题,满分40分)
9.已知x2+mx+16能用完全平方公式因式分解,则m的值为 .
10.因式分解:12x2y3﹣8x3y2+20x2y2= .
11.已知xy=﹣1,x+y=2,则x3y+2x2y2+xy3= .
12.化简:(a+2)(a2+4)(a4+16)(a﹣2)= .
13.多项式x2﹣8x+m=(x﹣9)(x﹣n),则m+n= .
14.若关于x的多项式(x+m)(2x﹣3)展开后不含x项,则m的值为 .
15.若(2022﹣a)(2021﹣a)=2020,则(2022﹣a)2+(2021﹣a)2= .
16.如图,小颖用4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若a=2b,则S1、S2之间存在的数量关系是 .
三.解答题(共5小题,满分40分)
17.计算:
(1)(x+2)(4x﹣2).
(2)(a+2b)(a2﹣4b2)(a﹣2b).
18.计算:(2x﹣3y)(3x+2y)﹣(2x﹣3y)2.
19.已知(x+y)2=7,(x﹣y)2=5.
(1)求x2+y2值;
(2)求xy的值.
20.因式分解:
(1)m3n﹣6m2n+9mn;
(2)4x2﹣(x2+1)2;
(3)利用因式分解计算:(﹣2)2022+(﹣2)2021﹣22020.
21.先化简,再求值:[(x﹣3y)2﹣(x﹣y)(x+y)+4xy]÷2y,其中x=﹣2,y=1.
22.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2),解答下列问题:
(1)设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2,请用含a,b的式子表示:S1= ,S2= ;(不必化简)
(2)由(1)中的结果可以验证的乘法公式是 ;
(3)利用(2)中得到的公式,计算:20212﹣2020×2022.
23.如图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分面积.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、m2 m3=m5,本选项计算错误,不符合题意;
B、m2+m2=2m2,本选项计算错误,不符合题意;
C、(﹣3a2b)2=9a4b2,本选项计算错误,不符合题意;
D、(﹣2x2) (﹣5x4)=10x6,本选项计算正确,符合题意;
故选:D.
2.解:A选项,等号右边不是积的形式,故该选项不符合题意;
B选项,10x2﹣5x=5x(2x﹣1),故该选项符合题意;
C选项,等号右边=x2﹣8x+16≠左边,故该选项不符合题意;
D选项,等号右边不是积的形式,故该选项不符合题意;
故选:B.
3.解:∵x +2x=3.
∴x (x +2x)=3x .
∴x4+2x =3x .
∴原式=x4+2x +5x +8x ﹣13x+15
=5x +3x +8x ﹣13x+15
=5x +10x +x ﹣13x+15
=5x(x +2x)+x ﹣13x+15
=5x×3+x ﹣13x+15
=x +2x+15
=3+15
=18.
故选:B.
4.解:(﹣2)2021+(﹣2)2020
=(﹣2)2020×(﹣2+1)
=﹣22020.
故选:B.
5.解:∵a=2020x+2019,b=2020x+2020,c=2020x+2021,
∴a﹣b=﹣1,a﹣c=﹣2,b﹣c=﹣1.
设S=a2+b2+c2﹣ab﹣ac﹣bc,
则2S=2a2+2b2+2c2﹣2ab﹣2ac﹣2bc.
∵2a2+2b2+2c2﹣2ab﹣2ac﹣2bc
=a2﹣2ab+b2+a2﹣2ac+c2+b2﹣2bc+c2
=(a﹣b)2+(a﹣c)2+(b﹣c)2
=(﹣1)2+(﹣2)2+(﹣1)2
=6,
∴S=3.
∴a2+b2+c2﹣ab﹣ac﹣bc=3.
故选:D.
6.解:(1)a2+b2,不符合题意;
(2)x2﹣y2=(x+y)(x﹣y),符合题意;
(3)﹣m2+n2
=n2﹣m2
=(n+m)(n﹣m),符合题意;
(4)﹣b2﹣a2=﹣(b2+a2),不符合题意;
(5)﹣a6+4.
=4﹣a6
=(4+a3)(4﹣a3),符合题意;
故选:B.
7.解:∵(x﹣1)(x5+x4+x3+x2+x+1)=0.
∴x6﹣1=0.
∴x6=1.
∴(x3)2=1.
∴x3=±1.
∴x=±1.
当x=1时,原式=12021﹣1=0.
当x=﹣1时,原式=12021﹣1=﹣2.
故选:D.
8.解:∵m2=2﹣n,n2=m+2,
∴m2﹣n2=(m+n)(m﹣n)=2﹣n﹣m﹣2=﹣(m+n),
∴m﹣n=﹣1,
∵m3=m m2=m(2﹣n)=2m﹣mn,n3=n n2=n(m+2)=mn+2n,
∴m3+2mn﹣n3=2m﹣mn+2mn﹣mn﹣2n=2(m﹣n)=﹣2,
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵x2+mx+16能用完全平方公式进行因式分解,x2+mx+16=x2+mx+42,
∴m=2×4=8或m=﹣(2×4)=﹣8,
∴m的值为±8.
故答案为:±8.
10.解:原式=4x2y2 3y﹣4x2y2 2x+4x2y2 5
=4x2y2(3y﹣2x+5).
故答案为:4x2y2(3y﹣2x+5).
11.解:∵xy=﹣1,x+y=2,
∴x3y+2x2y2+xy3
=xy(x2+2xy+y2)
=xy(x+y)2
=﹣1×22
=﹣4.
故答案为:﹣4.
12.解:(a+2)(a2+4)(a4+16)(a﹣2)
=(a+2)(a﹣2)(a2+4)(a4+16)
=(a2﹣4)(a2+4)(a4+16)
=(a4﹣16)(a4+16)
=a8﹣256.
故答案为:a8﹣256.
13.解:∵多项式x2﹣8x+m=(x﹣9)(x﹣n),
∴x2﹣8x+m=x +(﹣n﹣9)x+9n.
∴﹣n﹣9=﹣8,m=9n.
∴m=﹣9,n=﹣1.
∴m+n=﹣9+(﹣1)=﹣10.
故答案为:﹣10.
14.解:原式=2x2+(2m﹣3)x﹣3m,
∵多项式展开后不含x项,
∴2m﹣3=0,
∴m=;
故答案为:.
15.解:设x=2022﹣a,y=2021﹣a,
∴xy=2020,x﹣y=2022﹣a﹣2021+a=1,
∴(2022﹣a)2+(2021﹣a)2
=x2+y2
=(x﹣y)2+2xy
=1+2×2020
=4041.
故答案为:4041.
16.解:S1=b(a+b)×2+ab×2+(a﹣b)2=a2+2b2,
S2=(a+b)2﹣S1=(a+b)2﹣(a2+2b2)=2ab﹣b2,
∵a=2b,
∴S1=a2+2b2=6b2,S2=2ab﹣b2=3b2
∴S1=2S2.
故答案为:S1=2S2.
三.解答题(共7小题,满分40分)
17.解:(1)原式=4x2﹣2x+8x﹣4
=4x2+6x﹣4;
(2)原式=(a+2b)(a﹣2b)(a2﹣4b2)
=(a2﹣4b2)2
=a4﹣8a2b2+16b4.
.
18.解:原式=6x +4xy﹣9xy﹣6y ﹣(4x ﹣12xy+9y ).
=6x ﹣5xy﹣6y ﹣4x +12xy﹣9y .
=2x +7xy﹣15y .
19.解:(1)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①+②得:
x2+2xy+y2+x2﹣2xy+y2=12,
则x2+y2=6;
(2)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①﹣②得:
4xy=2,
解得:xy=
20.(1)m3n﹣6m2n+9mn=mn(m2﹣6m+9)=mn(m﹣3)2.
(2)4x2﹣(x2+1)2=(2x)2﹣(x2+1)2=(2x+x2+1)(2x﹣x2﹣1)=﹣(x2+2x+1)(x2﹣2x+1)
=﹣(x+1)2(x﹣1)2.
(3)原式=22022﹣22021﹣22020=22020(22﹣2﹣1)=22020.
21.解:原式=[x2﹣6xy+9y2﹣(x2﹣y2)+4xy]÷2y
=(x2﹣6xy+9y2﹣x2+y2+4xy)÷2y
=(﹣2xy+10y2)÷2y
=﹣x+5y,
当x=﹣2,y=1时,
原式=﹣(﹣2)+5×1
=2+5
=7.
22.解:(1)由题意得,S1=a2﹣b2,S2=(a+b)(a﹣b),
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由(1)中的结果可验证的乘法公式为(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b)=a2﹣b2;
(3)由(2)中所得乘法公式(a+b)(a﹣b)=a2﹣b2可得,
20212﹣2020×2022=20212﹣(2021+1)(2021﹣1)=20212﹣(20212﹣1)
=20212﹣20212+1
=1.
23.解:(1)由题意得:图2中阴影部分的正方形边长为:a﹣b.
故答案为:a﹣b.
(2)图2中阴影部分面积为:(a﹣b)2,还可以表示为:(a+b)2﹣4ab.
∴(a﹣b)2=(a+b)2﹣4ab.
(3)设AC=x,BC=y,由题意得:x+y=8,x2+y2=S1+S2=34.
∵(x+y)2=x2+y2+2xy.
∴64=34+2xy.
∴xy=15.
∴S阴影=AC CF=xy=7.5.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
