2021-2022学年青岛版八年级数学下册6.3特殊的平行四边形 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版八年级数学下册6.3特殊的平行四边形 同步练习题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 312.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 20:39:00 | ||
图片预览



文档简介
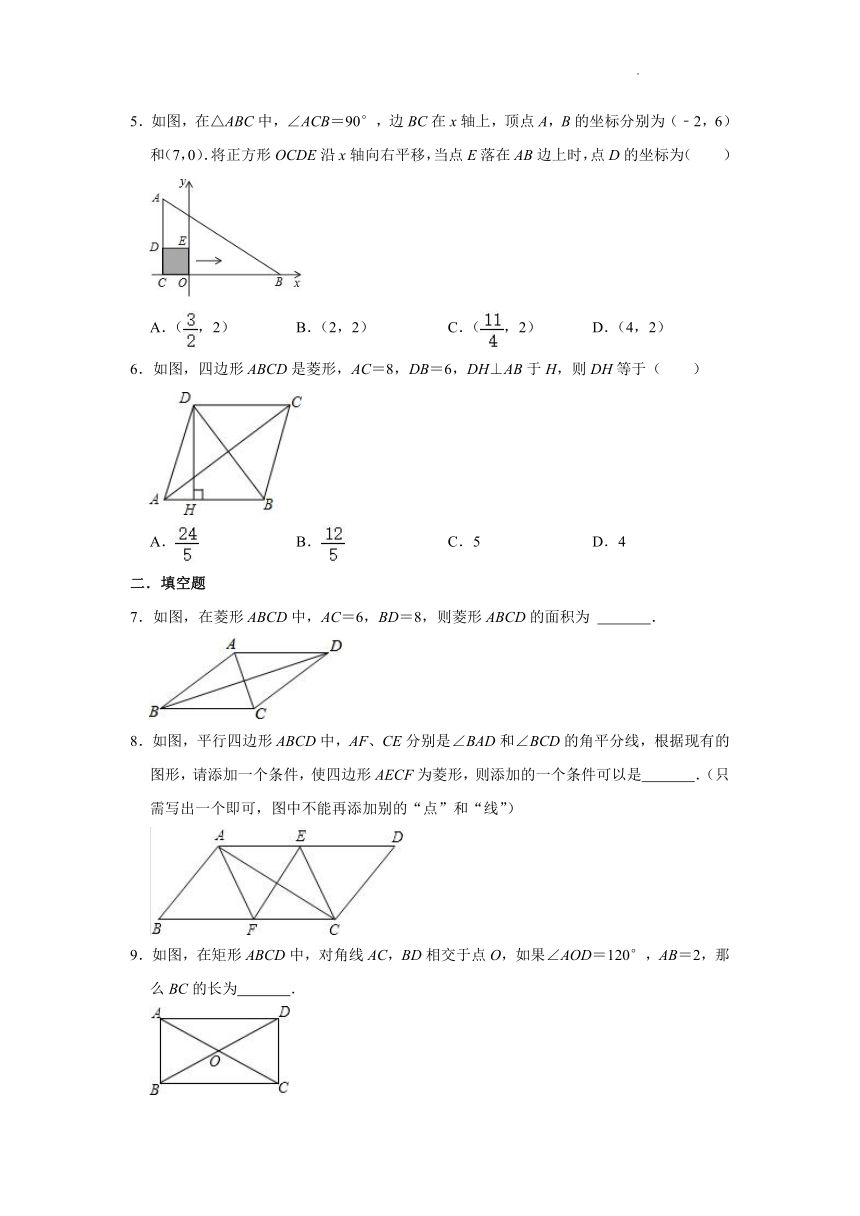
2021-2022学年青岛版八年级数学下册《6-3特殊的平行四边形》同步练习题(附答案)
一.选择题
1.如图,在菱形ABCD中,若∠B=60°,点E、F分别在AB、AD上,且BE=AF,则∠AEC+∠AFC的度数等于( )
A.120° B.140° C.160° D.180°
2.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
3.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减少
4.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )
A.20° B.25° C.30° D.35°
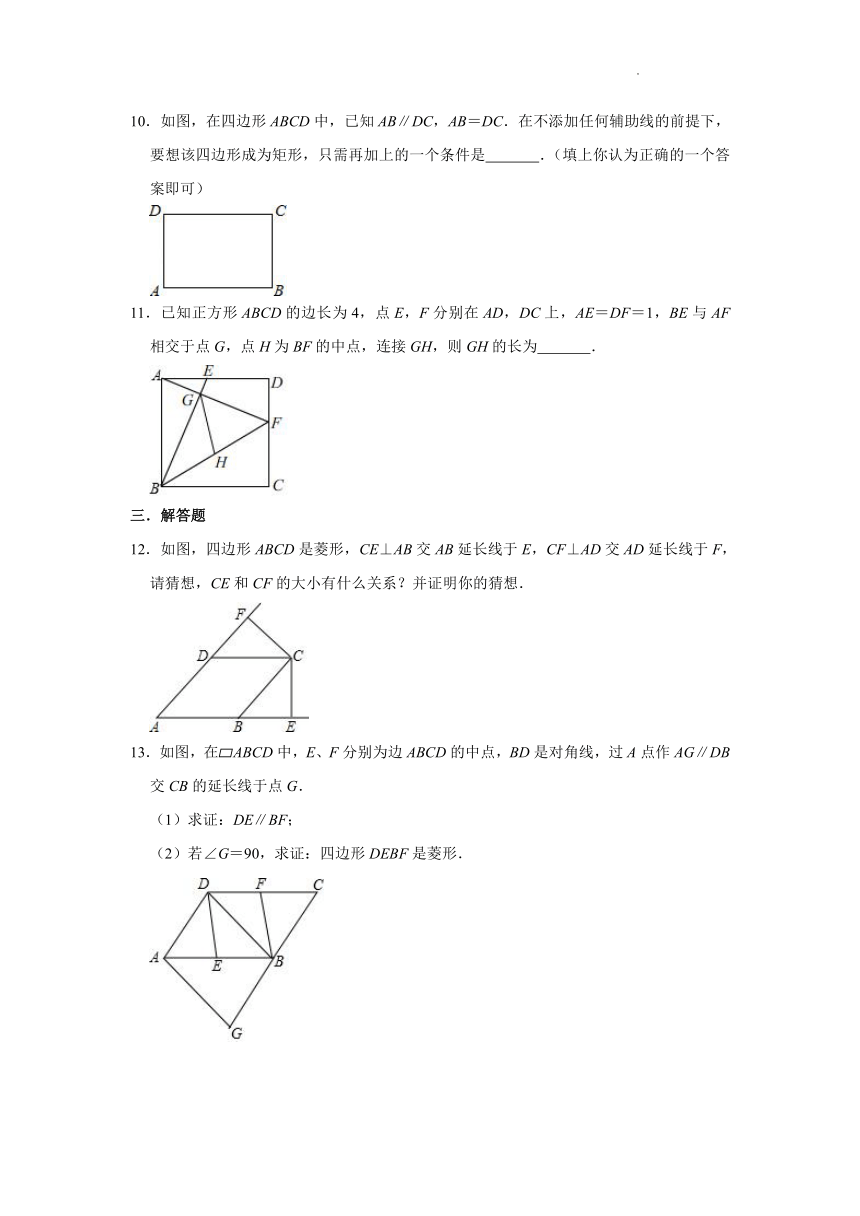
5.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )
A.(,2) B.(2,2) C.(,2) D.(4,2)
6.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
二.填空题
7.如图,在菱形ABCD中,AC=6,BD=8,则菱形ABCD的面积为 .
8.如图,平行四边形ABCD中,AF、CE分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是 .(只需写出一个即可,图中不能再添加别的“点”和“线”)
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,如果∠AOD=120°,AB=2,那么BC的长为 .
10.如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是 .(填上你认为正确的一个答案即可)
11.已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
三.解答题
12.如图,四边形ABCD是菱形,CE⊥AB交AB延长线于E,CF⊥AD交AD延长线于F,请猜想,CE和CF的大小有什么关系?并证明你的猜想.
13.如图,在 ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
14.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,求菱形BNDM的周长.
15.如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
16.如图,△ABC中,AB=AC,AD平分∠BAC交BC于点D,AE平分∠BAC的外角,且∠AEB=90°.求证:四边形ADBE是矩形.
17.如图,平行四边形ABCD中,对角线AC、BD交于点O,且AC⊥BC,点E是BC延长线上一点,,连接DE.
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
18.如图,已知在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
19.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
20.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由.
参考答案
一.选择题
1.解:连接AC,
∵在菱形ABCD中,∠B=60°,
∴AC=AB=BC=CD=AD,
∵BE=AF,
∴AE=DF,
∵∠B=60°,AC是对角线,
∴∠BAC=60°,
∴∠BAC=∠D=60°,
∴△ACE≌△CDF,
∴EC=FC.∠ACE=∠DCF,
∵∠DCF+∠ACF=60°,
∴∠ACE+∠ACF=60°,
∴△ECF是等边三角形.
故可得出∠ECF=60°,又∠EAF=120°,
∴∠AEC+∠AFC=360°﹣(60°+120°)=180°.
故选:D.
2.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
3.解:如图,连接AP.
∵∠A=90°,PE⊥AB,PF⊥AC
∴四边形AFPE是矩形,
∴EF=AP,
由垂线段最短可得AP⊥BC时,AP最短,则线段EF的值最小,
∴动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是先减小后增大.
故选:C.
4.解:∵AD∥BC,
∴∠AEB=∠DAE=∠B=80°,
∴AE=AB=AD,
在三角形AED中,AE=AD,∠DAE=80°,
∴∠ADE=50°,
又∵∠B=80°,
∴∠ADC=80°,
∴∠CDE=∠ADC﹣∠ADE=30°.
故选:C.
5.解:如图,设正方形D′C′O′E′是正方形OCDE沿x轴向右平移后的正方形,
∵顶点A,B的坐标分别为(﹣2,6)和(7,0),
∴AC=6,OC=2,OB=7,
∴BC=9,
∵四边形OCDE是正方形,
∴DE=OC=OE=2,
∴O′E′=O′C′=2,
∵E′O′⊥BC,
∴∠BO′E′=∠BCA=90°,
∴E′O′∥AC,
∴BO′=3,
∴OC′=7﹣2﹣3=2,
∴当点E落在AB边上时,点D的坐标为(2,2),
方法二:设直线AB的解析式为y=kx+b,
∵顶点A,B的坐标分别为(﹣2,6)和(7,0).
∴,
∴,
∴,
∵∠ACB=90°,边BC在x轴上,∴C点的坐标为(﹣2,0),
∴正方形OCDE的边长为2,
∴E(0,2),设点E沿x轴平移后落在AB边上的坐标为(a,2),
由y=﹣得,2=﹣a+,
∴a=4,
∴当点E落在AB边上时,点D的坐标为(2,2),
故选:B.
6.解:设AC交BD于O,
∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB==5,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
二.填空题
7.解:∵菱形ABCD的对角线AC=6,BD=8,
∴菱形ABCD的面积为:AC BD=×6×8=24.
故答案为:24.
8.解:则添加的一个条件可以是:AC⊥EF.
证明:∵AD∥BC,
∴∠FAD=∠AFB,
∵AF是∠BAD的平分线,
∴∠BAF=FAD,
∴∠BAF=∠AFB,
∴AB=BF,
同理ED=CD,
∵AD=BC,AB=CD,
∴AE=CF,
又∵AE∥CF
∴四边形AECF是平行四边形,
∵对角线互相平分且垂直的四边形是菱形,
则添加的一个条件可以是:AC⊥EF.
故答案为:AC⊥EF.
9.解:
∵∠AOD=120°,
∴∠AOB=60°,
∵四边形ABCD为矩形,
∴AO=OC=OB,
∴△AOB为等边三角形,
∴AO=OB=OC=AB=2,
∴AC=4,
在Rt△ABC中,由勾股定理可得BC=2,
故答案为:2.
10.解:添加的条件是∠A=90°,
理由是:∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形,
∵∠A=90°,
∴平行四边形ABCD是矩形,
故答案为:∠A=90°.
11.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=4、CF=CD﹣DF=4﹣1=3,
∴BF==5,
∴GH=BF=,
故答案为:.
三.解答题
12.解:CE=CF.
证明:∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,CD=BC.
∴∠A=∠CBE,∠A=∠FDC.
∴∠CBE=∠FDC.
∵CF⊥AD,CE⊥AB,
∴∠CEB=∠CFD=90°,
在△CDF和△CBE中,
∴△CDF≌△CBE(AAS).
∴CE=CF.
13.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、CD的中点,
∴DF=BE,又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE∥BF;
(2)∵AG∥DB,AD∥CG,
∴四边形AGBD是平行四边形,
∵∠G=90°,
∴平行四边形AGBD是矩形,
∴∠ADB=90°,又E为边AB的中点,
∴ED=EB,又四边形DEBF是平行四边形,
∴四边形DEBF是菱形.
14.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴四边形BNDM是菱形;
(2)解:∵四边形BNDM是菱形,BD=24,MN=10,
∴BM=BN=DM=DN,OB=BD=12,OM=MN=5,
在Rt△BOM中,由勾股定理得:BM===13,
∴菱形BNDM的周长=4BM=4×13=52.
15.解:(1)∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°﹣∠GFH,∠DHE=180°﹣∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
(2)连接EG,
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE∥BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.
16.证明:
∵AD是∠BAC的平分线,
∴∠1=∠2,
∵AE是∠BAF的平分线,
∴∠3=∠4,
∵∠1+∠2+∠3+4=180°,
∴∠2+∠3=90°,
即∠DAE=90°,
∵AB=AC,∠1=∠2,
∴AD⊥BC,
即∠ADB=90°,
∵∠AEB=90°,
∴四边形ADBE是矩形.
17.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵,
∴AD=CE,
∴四边形ACED是平行四边形,
∵AC⊥BC,
∴∠ACE=90°,
∴四边形ACED是矩形;
(2)∵对角线AC,BD交于点O,
∴点O是BD的中点,
∵四边形ACED是矩形,
∴∠BED=90°,
∴OE=BD,
∴OE=5,
18.证明;(1)∵四边形ABCD是平行四边形,
∴AO=CO=AC,
∵EA=EC,
∴EO⊥AC,
即BD⊥AC,
∴平行四边形ABCD是菱形;
(2)∵∠1=∠EAD+∠AED,∠DAC=∠EAD+∠AED,
∴∠1=∠DAC,
∴AO=DO,
∵四边形ABCD是菱形,
∴AC=2AO,DB=2DO,
∴AC=BD,
∴四边形ABCD是正方形.
19.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,
∴∠BAD=∠ABC,
∴2∠BAD=180°,∴∠BAD=90°,
∴四边形ABCD是正方形;
(2)证明:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,CO=AC,DO=BD,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,
∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH,
在△ECO和△FDO中,,
∴△ECO≌△FDO(ASA),
∴OE=OF.
20.解:(1)①CF⊥BD,CF=BD
故答案为:垂直、相等.
②成立,理由如下:
∵∠FAD=∠BAC=90°
∴∠BAD=∠CAF
在△BAD与△CAF中,
∵
∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ACB=45°,
∴∠BCF=90°
∴CF⊥BD
(2)当∠ACB=45°时可得CF⊥BC,理由如下:
过点A作AC的垂线与CB所在直线交于G
则∵∠ACB=45°
∴AG=AC,∠AGC=∠ACG=45°
∵AG=AC,AD=AF,
∵∠GAD=∠GAC﹣∠DAC=90°﹣∠DAC,∠FAC=∠FAD﹣∠DAC=90°﹣∠DAC,
∴∠GAD=∠FAC,
∴△GAD≌△CAF(SAS)
∴∠ACF=∠AGD=45°
∴∠GCF=∠GCA+∠ACF=90°
∴CF⊥BC
一.选择题
1.如图,在菱形ABCD中,若∠B=60°,点E、F分别在AB、AD上,且BE=AF,则∠AEC+∠AFC的度数等于( )
A.120° B.140° C.160° D.180°
2.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
3.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减少
4.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )
A.20° B.25° C.30° D.35°
5.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )
A.(,2) B.(2,2) C.(,2) D.(4,2)
6.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
二.填空题
7.如图,在菱形ABCD中,AC=6,BD=8,则菱形ABCD的面积为 .
8.如图,平行四边形ABCD中,AF、CE分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是 .(只需写出一个即可,图中不能再添加别的“点”和“线”)
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,如果∠AOD=120°,AB=2,那么BC的长为 .
10.如图,在四边形ABCD中,已知AB∥DC,AB=DC.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是 .(填上你认为正确的一个答案即可)
11.已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
三.解答题
12.如图,四边形ABCD是菱形,CE⊥AB交AB延长线于E,CF⊥AD交AD延长线于F,请猜想,CE和CF的大小有什么关系?并证明你的猜想.
13.如图,在 ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
14.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,求菱形BNDM的周长.
15.如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
16.如图,△ABC中,AB=AC,AD平分∠BAC交BC于点D,AE平分∠BAC的外角,且∠AEB=90°.求证:四边形ADBE是矩形.
17.如图,平行四边形ABCD中,对角线AC、BD交于点O,且AC⊥BC,点E是BC延长线上一点,,连接DE.
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
18.如图,已知在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.
19.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
20.如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?并说明理由.
参考答案
一.选择题
1.解:连接AC,
∵在菱形ABCD中,∠B=60°,
∴AC=AB=BC=CD=AD,
∵BE=AF,
∴AE=DF,
∵∠B=60°,AC是对角线,
∴∠BAC=60°,
∴∠BAC=∠D=60°,
∴△ACE≌△CDF,
∴EC=FC.∠ACE=∠DCF,
∵∠DCF+∠ACF=60°,
∴∠ACE+∠ACF=60°,
∴△ECF是等边三角形.
故可得出∠ECF=60°,又∠EAF=120°,
∴∠AEC+∠AFC=360°﹣(60°+120°)=180°.
故选:D.
2.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
3.解:如图,连接AP.
∵∠A=90°,PE⊥AB,PF⊥AC
∴四边形AFPE是矩形,
∴EF=AP,
由垂线段最短可得AP⊥BC时,AP最短,则线段EF的值最小,
∴动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是先减小后增大.
故选:C.
4.解:∵AD∥BC,
∴∠AEB=∠DAE=∠B=80°,
∴AE=AB=AD,
在三角形AED中,AE=AD,∠DAE=80°,
∴∠ADE=50°,
又∵∠B=80°,
∴∠ADC=80°,
∴∠CDE=∠ADC﹣∠ADE=30°.
故选:C.
5.解:如图,设正方形D′C′O′E′是正方形OCDE沿x轴向右平移后的正方形,
∵顶点A,B的坐标分别为(﹣2,6)和(7,0),
∴AC=6,OC=2,OB=7,
∴BC=9,
∵四边形OCDE是正方形,
∴DE=OC=OE=2,
∴O′E′=O′C′=2,
∵E′O′⊥BC,
∴∠BO′E′=∠BCA=90°,
∴E′O′∥AC,
∴BO′=3,
∴OC′=7﹣2﹣3=2,
∴当点E落在AB边上时,点D的坐标为(2,2),
方法二:设直线AB的解析式为y=kx+b,
∵顶点A,B的坐标分别为(﹣2,6)和(7,0).
∴,
∴,
∴,
∵∠ACB=90°,边BC在x轴上,∴C点的坐标为(﹣2,0),
∴正方形OCDE的边长为2,
∴E(0,2),设点E沿x轴平移后落在AB边上的坐标为(a,2),
由y=﹣得,2=﹣a+,
∴a=4,
∴当点E落在AB边上时,点D的坐标为(2,2),
故选:B.
6.解:设AC交BD于O,
∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB==5,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
二.填空题
7.解:∵菱形ABCD的对角线AC=6,BD=8,
∴菱形ABCD的面积为:AC BD=×6×8=24.
故答案为:24.
8.解:则添加的一个条件可以是:AC⊥EF.
证明:∵AD∥BC,
∴∠FAD=∠AFB,
∵AF是∠BAD的平分线,
∴∠BAF=FAD,
∴∠BAF=∠AFB,
∴AB=BF,
同理ED=CD,
∵AD=BC,AB=CD,
∴AE=CF,
又∵AE∥CF
∴四边形AECF是平行四边形,
∵对角线互相平分且垂直的四边形是菱形,
则添加的一个条件可以是:AC⊥EF.
故答案为:AC⊥EF.
9.解:
∵∠AOD=120°,
∴∠AOB=60°,
∵四边形ABCD为矩形,
∴AO=OC=OB,
∴△AOB为等边三角形,
∴AO=OB=OC=AB=2,
∴AC=4,
在Rt△ABC中,由勾股定理可得BC=2,
故答案为:2.
10.解:添加的条件是∠A=90°,
理由是:∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形,
∵∠A=90°,
∴平行四边形ABCD是矩形,
故答案为:∠A=90°.
11.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=4、CF=CD﹣DF=4﹣1=3,
∴BF==5,
∴GH=BF=,
故答案为:.
三.解答题
12.解:CE=CF.
证明:∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,CD=BC.
∴∠A=∠CBE,∠A=∠FDC.
∴∠CBE=∠FDC.
∵CF⊥AD,CE⊥AB,
∴∠CEB=∠CFD=90°,
在△CDF和△CBE中,
∴△CDF≌△CBE(AAS).
∴CE=CF.
13.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、CD的中点,
∴DF=BE,又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE∥BF;
(2)∵AG∥DB,AD∥CG,
∴四边形AGBD是平行四边形,
∵∠G=90°,
∴平行四边形AGBD是矩形,
∴∠ADB=90°,又E为边AB的中点,
∴ED=EB,又四边形DEBF是平行四边形,
∴四边形DEBF是菱形.
14.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴四边形BNDM是菱形;
(2)解:∵四边形BNDM是菱形,BD=24,MN=10,
∴BM=BN=DM=DN,OB=BD=12,OM=MN=5,
在Rt△BOM中,由勾股定理得:BM===13,
∴菱形BNDM的周长=4BM=4×13=52.
15.解:(1)∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°﹣∠GFH,∠DHE=180°﹣∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
(2)连接EG,
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE∥BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.
16.证明:
∵AD是∠BAC的平分线,
∴∠1=∠2,
∵AE是∠BAF的平分线,
∴∠3=∠4,
∵∠1+∠2+∠3+4=180°,
∴∠2+∠3=90°,
即∠DAE=90°,
∵AB=AC,∠1=∠2,
∴AD⊥BC,
即∠ADB=90°,
∵∠AEB=90°,
∴四边形ADBE是矩形.
17.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵,
∴AD=CE,
∴四边形ACED是平行四边形,
∵AC⊥BC,
∴∠ACE=90°,
∴四边形ACED是矩形;
(2)∵对角线AC,BD交于点O,
∴点O是BD的中点,
∵四边形ACED是矩形,
∴∠BED=90°,
∴OE=BD,
∴OE=5,
18.证明;(1)∵四边形ABCD是平行四边形,
∴AO=CO=AC,
∵EA=EC,
∴EO⊥AC,
即BD⊥AC,
∴平行四边形ABCD是菱形;
(2)∵∠1=∠EAD+∠AED,∠DAC=∠EAD+∠AED,
∴∠1=∠DAC,
∴AO=DO,
∵四边形ABCD是菱形,
∴AC=2AO,DB=2DO,
∴AC=BD,
∴四边形ABCD是正方形.
19.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,
∴∠BAD=∠ABC,
∴2∠BAD=180°,∴∠BAD=90°,
∴四边形ABCD是正方形;
(2)证明:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,CO=AC,DO=BD,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,
∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH,
在△ECO和△FDO中,,
∴△ECO≌△FDO(ASA),
∴OE=OF.
20.解:(1)①CF⊥BD,CF=BD
故答案为:垂直、相等.
②成立,理由如下:
∵∠FAD=∠BAC=90°
∴∠BAD=∠CAF
在△BAD与△CAF中,
∵
∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ACB=45°,
∴∠BCF=90°
∴CF⊥BD
(2)当∠ACB=45°时可得CF⊥BC,理由如下:
过点A作AC的垂线与CB所在直线交于G
则∵∠ACB=45°
∴AG=AC,∠AGC=∠ACG=45°
∵AG=AC,AD=AF,
∵∠GAD=∠GAC﹣∠DAC=90°﹣∠DAC,∠FAC=∠FAD﹣∠DAC=90°﹣∠DAC,
∴∠GAD=∠FAC,
∴△GAD≌△CAF(SAS)
∴∠ACF=∠AGD=45°
∴∠GCF=∠GCA+∠ACF=90°
∴CF⊥BC
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
