2021-2022学年青岛版八年级数学下册6.4三角形的中位线定理 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版八年级数学下册6.4三角形的中位线定理 同步练习题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 544.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 00:00:00 | ||
图片预览





文档简介
2021-2022学年青岛版八年级数学下册《6-4三角形的中位线》同步练习题(附答案)
一.选择题
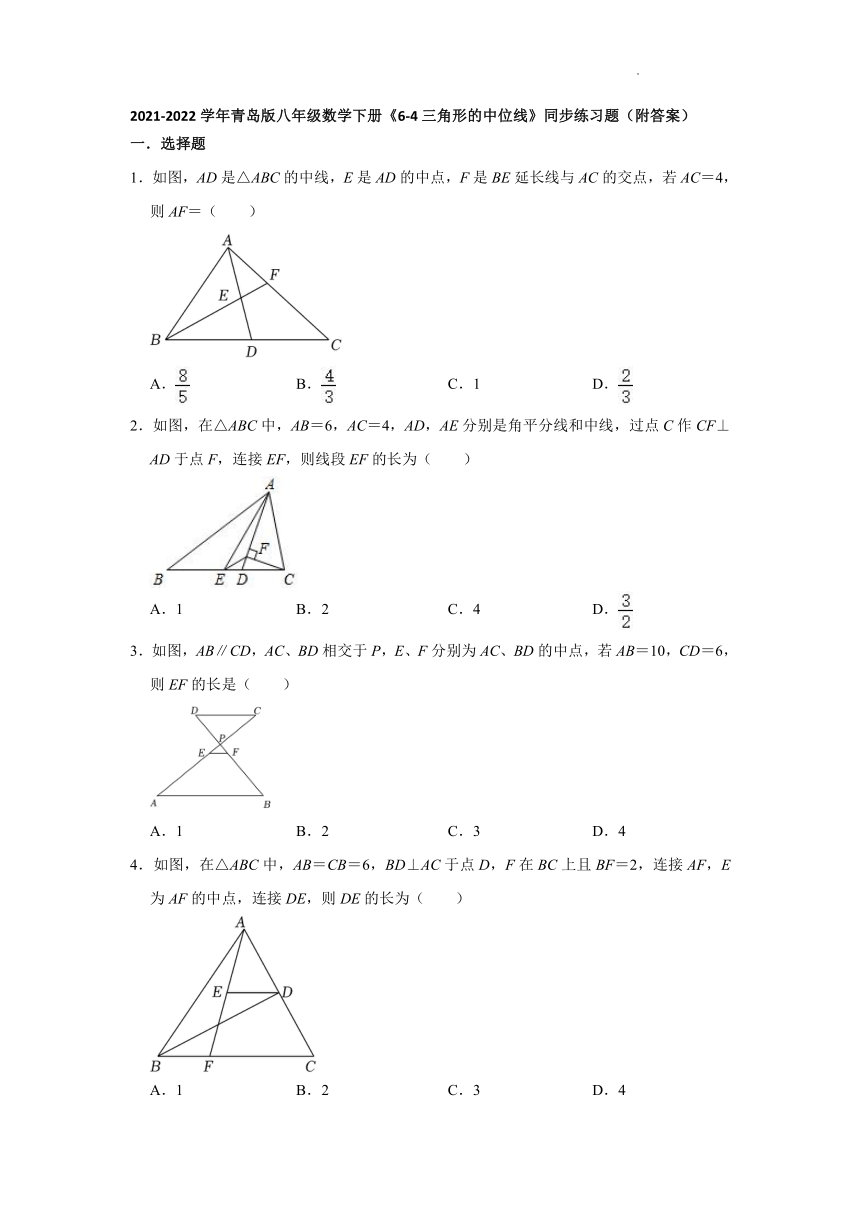
1.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF=( )
A. B. C.1 D.
2.如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为( )
A.1 B.2 C.4 D.
3.如图,AB∥CD,AC、BD相交于P,E、F分别为AC、BD的中点,若AB=10,CD=6,则EF的长是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,AB=CB=6,BD⊥AC于点D,F在BC上且BF=2,连接AF,E为AF的中点,连接DE,则DE的长为( )
A.1 B.2 C.3 D.4
5.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
6.如图所示,已知四边形ABCD,R、P分别是DC、BC上的点,点E、F分别是AP、RP的中点,当点P在边BC上从点B向点C移动,且点R从点D向点C移动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减少
C.线段EF的长不变
D.△ABP和△CRP的面积和不变
7.如图,△ABC中,点D,E在边BC上,∠ABC平分线垂直AE,垂足为点N,∠ACB的平分线垂直AD,垂足为点M,连接MN.若BC=7,MN=,则△ABC的周长为( )
A.17 B.18 C.19 D.20
8.如图,已知△ABC中AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④∠DAE=90°.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图,四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是( )
A.AD+BC>2EF B.AD+BC≥2EF C.AD+BC<2EF D.AD+BC≤2EF
10.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=4cm,则AF的长度是( )
A.2cm B.3cm C.4cm D.6cm
11.如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
12.如图,在△ABC中,点D、E分别是AB、AC的中点,AC=10,点F是DE上一点.DF=1.连接AF,CF.若∠AFC=90°,则BC的长度为( )
A.18 B.16 C.14 D.12
13.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为( )
A.2 B.5 C.7 D.9
14.如图,△ABC的周长为20,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=8,则MN的长度为( )
A. B.2 C. D.3
二.填空题
15.如图,点M,N分别是△ABC的边AB,AC的中点,若∠A=60°,∠B=75°,则∠ANM= .
16.如图,在平面直角坐标系中,△ABC的顶点B、C的坐标分别是(﹣1,0),(5,0),点D、E分别是AB、AC的中点,点D的坐标为(1,2),则点A、E的坐标分别是 .
17.如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,DE∥AC交AB于点E,若DE=3,则AB= .
18.如图,已知在△ABC中,AB=3,AC=5,D、E分别是AB、AC的中点,连结DE.若DE=2,则△ABC的面积是 .
19.已知在△ABC中,AC=6cm,点D、E分别是AC、BC的中点,连接DE,在DE上有一点F,EF=1cm,连接AF,CF,若AF⊥CF,则AB= .
20.如图,△ABC中,D、E分别是AB、AC的中点,若DE=4cm,则BC= cm.
21.顺次联接三角形三边中点,所得到的三角形与原三角形的周长的比是 .
22.如图,△ABC中,D是BC中点,AE平分∠BAC,AE⊥BE,AB=3,AC=5,则DE= .
23.如图,在△ABC中,点D、E分别是AB、AC边的中点,若BC=6cm,则线段DE= cm.
24.已知△ABC的周长是2,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2021个三角形周长是 .
25.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为 .如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是 .
三.解答题
26.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
27.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.若BD平分∠ABC,求证:BD⊥AC.
28.如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点.求证:BD=2EF.
29.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
参考答案
一.选择题
1.解:取EF的中点H,连接DH,
∵BD=DC,BH=HF,
∴DH=FC,DH∥AC,
∴∠HDE=∠FAE,
在△AEF和△DEH中,
,
∴△AEF≌△DEH(ASA),
∴AF=DH,
∴AF=FC,
∵AC=4,
∴AF=,故选:B.
2.解:延长CF交AB于G,
∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形,
∴AG=AC=4,FG=CF,
∴BG=AB﹣AG=6﹣4=2,
∵AE为△ABC的中线,
∴EF是△BCG的中位线,
∴EF=BG=1,故选:A.
3.解:连接CF并延长,交AB于G,
∵AB∥DC,
∴∠D=∠B,
∵F为BD的中点,
∴DF=BF,
在△DFC和△BFG中,
,
∴△DFC≌△BFG(ASA),
∴BG=CD=6,CF=FG,
∴AG=AB﹣BG=4,
∵CF=FG,CE=EA,
∴EF=AG=×4=2,
故选:B.
4.解:∵CB=6,BF=2,
∴FC=6﹣2=4,
∵BA=BC,BD⊥AC,
∴AD=DC,
∵AE=EF,
∴DE是△AFC的中位线,
∴DE=FC=×4=2,
故选:B.
5.解:∵点A1、B1、C1分别为BC、AC、AB的中点,
∴B1C1=BC,A1C1=AC,A1B1=AB,
∴△A1B1C1的周长=a,
同理,△A2B2C2的周长=a=a,
……
则△AnBn n的周长=a,
故选:A.
6.解:连接AR,
∵E,F分别是AP,RP的中点,
∴EF=AR,
∵当点P在BC上从点C向点B移动,点R从点D向点C移动时,AR的长度逐渐增大,
∴线段EF的长逐渐增大.
S△ABP+S△CRP=BC (AB+CR).
∵CR随着点R的运动而减小,
∴△ABP和△CRP的面积和逐渐减小.
观察选项,只有选项A符合题意.
故选:A.
7.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=,
∴DE=2MN=3,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=10,
∴△ABC的周长=AB+AC+BC=10+7=17,
故选:A.
8.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴∠DAE=90°,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
9.解:如图,取AC的中点G,连接EF,EG,GF,
∵E,F分别是边AB,CD的中点,
∴EG,GF分别是△ABC和△ACD的中位线,
∴EG=BC,GF=AD,
在△EGF中,由三角形三边关系得EG+GF>EF,即BC+AD>EF,
∴AD+BC>2EF,
当AD∥BC时,点E、F、G在同一条直线上,
∴AD+BC=2EF,
所以四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是AD+BC≥2EF.
故选:B.
10.解:∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=8cm,
在Rt△BAC中,点F分别是斜边BC的中点,
则AF=BC=4cm,
故选:C.
11.解:连接AF并延长交BC于H,如图所示:
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=6,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=8,
∵AD=DB,AF=FH,
∴DF是△ABH的中位线,
∴DF=BH=4,
∴EF=DE﹣DF=2,
故选:C.
12.解:∵∠AFC=90°,点E是AC的中点,AC=10,
∴EF=AC=×10=5,
∵DF=1,
∴DE=DF+EF=6,
∵点D、E分别是AB、AC的中点,
∴BC=2DE=12,
故选:D.
13.解:连接DN,
∵ED=EM,MF=FN,
∴EF=DN,
∴DN最大时,EF最大,DN最小时,EF最小,
∵N与B重合时DN最大,
此时DN=DB===13,
∴EF的最大值为6.5.
∵∠A=90°,AD=5,
∴DN≥5,
∴EF≥2.5,
∴EF长度的可能为5;
故选:B.
14.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA)
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∴DE=BE+CD﹣BC=BA+CA﹣BC=20﹣8﹣8=4,
∵AN=NE,AM=MD,
∴MN=DE=2,
故选:B.
二.填空题
15.解:在△ABC中,∠A=60°,∠B=75°,
则∠C=180°﹣∠A﹣∠B=180°﹣60°﹣75°=45°,
∵点M,N分别是△ABC的边AB,AC的中点,
∴MN是△ABC的中位线,
∴MN∥BC,
∴∠ANM=∠C=45°,
故答案为:45°.
16.解:∵点B、C的坐标分别是(﹣1,0),(5,0),
∴BC=6.
∵点D、E分别是AB、AC的中点,
∴DE∥BC,且DE=BC=3.
又∵点D的坐标为(1,2),
∴点E的坐标为(4,2).
设直线AB表达式为:y=kx+b(k≠0),
把点B、D的坐标分别代入,得.
解得.
故直线AB的表达式为y=x+1.
同理,直线AC的表达为:y=﹣2x+10.
所以.
解得.
故A(3,4).
故答案是:(3,4)、(4,2).
17.解:延长AC交BD的延长线于点F,
在△ADB和△ADF中,
,
∴△ADB≌△ADF(ASA),
∴BD=DF,AB=AF,
∵DE∥AC,BD=DF,
∴AF=2DE=2×3=6,
∴AB=6,
故答案为:6.
18.解:∵D,E分别是AB,AC的中点,DE=2,
∴BC=2DE=4,
∵AB2+BC2=32+42=52=AC2,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,
∴S△ABC= AC BC=×3×4=6,
故答案为:6.
19.解:在Rt△AFC中,点D是AC的中点,AC=6cm,
∴DF=AC=×6=3(cm),
∵EF=1cm,
∴DE=DF+EF=3+1=4(cm),
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×4=8(cm),
故答案为:8cm.
20.解:∵D,E分别是△ABC的边AB和AC的中点,
∴DE是△ABC的中位线,
∵DE=4cm,
∴BC=2DE=8(cm).
故答案为:8.
21.解:如图,∵D、E、F分别是AB、BC、AC的中点,
∴DE=AC,DF=BC,EF=AB,
∴DE+DF+EF=AC+BC+AB,
∵△DEF∽△ABC,
∴所得到的△DEF与△ABC的周长之比是.
故答案为:.
22.解:延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠FAE,
∵AE⊥BE,
∴∠AEB=∠AEF=90°,
在△AEB和△AEF中,
,
∴△AEB≌△AEF(ASA),
∴AF=AB=3,BE=EF,
∴FC=AC﹣AF=5﹣3=2,
∵BD=DC,BE=EF,
∴DE=FC=1,
故答案为:1.
23.解:∵点D,点E分别是AB,AC边的中点,
∴DE是△ABC的中位线,
∴DE=BC=×6=3(cm),
故答案为:3.
24.解:∵D、E、F分别为AB、BC、AC的中点,
∴DE=AC,DF=BC,EF=AB,
∵△ABC的周长是2,
∴AB+AC+BC=2,
∴△DEF的周长=EF+DE+DF=×(AB+AC+BC)=1=2×,
同理可得:第三个三角形的周长=2×,
……
则第2021个三角形周长=2×=,
故答案为:.
25.解:∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半.
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16.
以此类推,第n个小三角形的周长是第一个三角形周长的64×()n﹣1=27﹣n
故答案是:27﹣n.
三.解答题
26.解:(1)由题意得:OC∥AD,
∵点C为AB的中点,
∴OC为△ABD的中位线,
∴OC=AD,
∵AD=1米,
∴OC=米;
(2)要把小聪最高翘到1.25米高,立柱OC的高度要升高为0.625米.
当AD=1.25米时,OC=0.625米,
所以要把小聪最高翘到1.25米高,立柱OC的高度要升高为0.625米.
27.证明:∵D,E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∵BD平分∠ABC,
∴∠CBD=∠EBD,
∵DE∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴DE=BE,
∵AB=2BE,
∴AB=2DE,
∴AB=BC,
∵点D是AC的中点,
∴BD⊥AC.
28.证明:∵AD=AC,AE⊥CD,
∴CE=ED,
∵F是BC的中点,
∴EF是△CDB的中位线,
∴BD=2EF.
29.(1)解:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,AB=6,CD=8,
∴PE∥AB,且PE=AB=3,PF∥CD且PF=CD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在直角△EPF中,由勾股定理得到:EF===5,
即EF=5;
(2)证明:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,
∴PE∥AB,且PE=AB,PF∥CD且PF=CD.
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°﹣∠BPF=180°﹣∠BDC,
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴PE2+PF2=(AB)2+(CD)2=EF2,
∴AB2+CD2=4EF2.
一.选择题
1.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF=( )
A. B. C.1 D.
2.如图,在△ABC中,AB=6,AC=4,AD,AE分别是角平分线和中线,过点C作CF⊥AD于点F,连接EF,则线段EF的长为( )
A.1 B.2 C.4 D.
3.如图,AB∥CD,AC、BD相交于P,E、F分别为AC、BD的中点,若AB=10,CD=6,则EF的长是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,AB=CB=6,BD⊥AC于点D,F在BC上且BF=2,连接AF,E为AF的中点,连接DE,则DE的长为( )
A.1 B.2 C.3 D.4
5.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
6.如图所示,已知四边形ABCD,R、P分别是DC、BC上的点,点E、F分别是AP、RP的中点,当点P在边BC上从点B向点C移动,且点R从点D向点C移动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减少
C.线段EF的长不变
D.△ABP和△CRP的面积和不变
7.如图,△ABC中,点D,E在边BC上,∠ABC平分线垂直AE,垂足为点N,∠ACB的平分线垂直AD,垂足为点M,连接MN.若BC=7,MN=,则△ABC的周长为( )
A.17 B.18 C.19 D.20
8.如图,已知△ABC中AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④∠DAE=90°.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图,四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是( )
A.AD+BC>2EF B.AD+BC≥2EF C.AD+BC<2EF D.AD+BC≤2EF
10.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=4cm,则AF的长度是( )
A.2cm B.3cm C.4cm D.6cm
11.如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
12.如图,在△ABC中,点D、E分别是AB、AC的中点,AC=10,点F是DE上一点.DF=1.连接AF,CF.若∠AFC=90°,则BC的长度为( )
A.18 B.16 C.14 D.12
13.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为( )
A.2 B.5 C.7 D.9
14.如图,△ABC的周长为20,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=8,则MN的长度为( )
A. B.2 C. D.3
二.填空题
15.如图,点M,N分别是△ABC的边AB,AC的中点,若∠A=60°,∠B=75°,则∠ANM= .
16.如图,在平面直角坐标系中,△ABC的顶点B、C的坐标分别是(﹣1,0),(5,0),点D、E分别是AB、AC的中点,点D的坐标为(1,2),则点A、E的坐标分别是 .
17.如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,DE∥AC交AB于点E,若DE=3,则AB= .
18.如图,已知在△ABC中,AB=3,AC=5,D、E分别是AB、AC的中点,连结DE.若DE=2,则△ABC的面积是 .
19.已知在△ABC中,AC=6cm,点D、E分别是AC、BC的中点,连接DE,在DE上有一点F,EF=1cm,连接AF,CF,若AF⊥CF,则AB= .
20.如图,△ABC中,D、E分别是AB、AC的中点,若DE=4cm,则BC= cm.
21.顺次联接三角形三边中点,所得到的三角形与原三角形的周长的比是 .
22.如图,△ABC中,D是BC中点,AE平分∠BAC,AE⊥BE,AB=3,AC=5,则DE= .
23.如图,在△ABC中,点D、E分别是AB、AC边的中点,若BC=6cm,则线段DE= cm.
24.已知△ABC的周长是2,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2021个三角形周长是 .
25.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为 .如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是 .
三.解答题
26.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
27.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.若BD平分∠ABC,求证:BD⊥AC.
28.如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点.求证:BD=2EF.
29.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
参考答案
一.选择题
1.解:取EF的中点H,连接DH,
∵BD=DC,BH=HF,
∴DH=FC,DH∥AC,
∴∠HDE=∠FAE,
在△AEF和△DEH中,
,
∴△AEF≌△DEH(ASA),
∴AF=DH,
∴AF=FC,
∵AC=4,
∴AF=,故选:B.
2.解:延长CF交AB于G,
∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形,
∴AG=AC=4,FG=CF,
∴BG=AB﹣AG=6﹣4=2,
∵AE为△ABC的中线,
∴EF是△BCG的中位线,
∴EF=BG=1,故选:A.
3.解:连接CF并延长,交AB于G,
∵AB∥DC,
∴∠D=∠B,
∵F为BD的中点,
∴DF=BF,
在△DFC和△BFG中,
,
∴△DFC≌△BFG(ASA),
∴BG=CD=6,CF=FG,
∴AG=AB﹣BG=4,
∵CF=FG,CE=EA,
∴EF=AG=×4=2,
故选:B.
4.解:∵CB=6,BF=2,
∴FC=6﹣2=4,
∵BA=BC,BD⊥AC,
∴AD=DC,
∵AE=EF,
∴DE是△AFC的中位线,
∴DE=FC=×4=2,
故选:B.
5.解:∵点A1、B1、C1分别为BC、AC、AB的中点,
∴B1C1=BC,A1C1=AC,A1B1=AB,
∴△A1B1C1的周长=a,
同理,△A2B2C2的周长=a=a,
……
则△AnBn n的周长=a,
故选:A.
6.解:连接AR,
∵E,F分别是AP,RP的中点,
∴EF=AR,
∵当点P在BC上从点C向点B移动,点R从点D向点C移动时,AR的长度逐渐增大,
∴线段EF的长逐渐增大.
S△ABP+S△CRP=BC (AB+CR).
∵CR随着点R的运动而减小,
∴△ABP和△CRP的面积和逐渐减小.
观察选项,只有选项A符合题意.
故选:A.
7.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=,
∴DE=2MN=3,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=10,
∴△ABC的周长=AB+AC+BC=10+7=17,
故选:A.
8.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴∠DAE=90°,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
9.解:如图,取AC的中点G,连接EF,EG,GF,
∵E,F分别是边AB,CD的中点,
∴EG,GF分别是△ABC和△ACD的中位线,
∴EG=BC,GF=AD,
在△EGF中,由三角形三边关系得EG+GF>EF,即BC+AD>EF,
∴AD+BC>2EF,
当AD∥BC时,点E、F、G在同一条直线上,
∴AD+BC=2EF,
所以四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是AD+BC≥2EF.
故选:B.
10.解:∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=8cm,
在Rt△BAC中,点F分别是斜边BC的中点,
则AF=BC=4cm,
故选:C.
11.解:连接AF并延长交BC于H,如图所示:
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=6,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=8,
∵AD=DB,AF=FH,
∴DF是△ABH的中位线,
∴DF=BH=4,
∴EF=DE﹣DF=2,
故选:C.
12.解:∵∠AFC=90°,点E是AC的中点,AC=10,
∴EF=AC=×10=5,
∵DF=1,
∴DE=DF+EF=6,
∵点D、E分别是AB、AC的中点,
∴BC=2DE=12,
故选:D.
13.解:连接DN,
∵ED=EM,MF=FN,
∴EF=DN,
∴DN最大时,EF最大,DN最小时,EF最小,
∵N与B重合时DN最大,
此时DN=DB===13,
∴EF的最大值为6.5.
∵∠A=90°,AD=5,
∴DN≥5,
∴EF≥2.5,
∴EF长度的可能为5;
故选:B.
14.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA)
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∴DE=BE+CD﹣BC=BA+CA﹣BC=20﹣8﹣8=4,
∵AN=NE,AM=MD,
∴MN=DE=2,
故选:B.
二.填空题
15.解:在△ABC中,∠A=60°,∠B=75°,
则∠C=180°﹣∠A﹣∠B=180°﹣60°﹣75°=45°,
∵点M,N分别是△ABC的边AB,AC的中点,
∴MN是△ABC的中位线,
∴MN∥BC,
∴∠ANM=∠C=45°,
故答案为:45°.
16.解:∵点B、C的坐标分别是(﹣1,0),(5,0),
∴BC=6.
∵点D、E分别是AB、AC的中点,
∴DE∥BC,且DE=BC=3.
又∵点D的坐标为(1,2),
∴点E的坐标为(4,2).
设直线AB表达式为:y=kx+b(k≠0),
把点B、D的坐标分别代入,得.
解得.
故直线AB的表达式为y=x+1.
同理,直线AC的表达为:y=﹣2x+10.
所以.
解得.
故A(3,4).
故答案是:(3,4)、(4,2).
17.解:延长AC交BD的延长线于点F,
在△ADB和△ADF中,
,
∴△ADB≌△ADF(ASA),
∴BD=DF,AB=AF,
∵DE∥AC,BD=DF,
∴AF=2DE=2×3=6,
∴AB=6,
故答案为:6.
18.解:∵D,E分别是AB,AC的中点,DE=2,
∴BC=2DE=4,
∵AB2+BC2=32+42=52=AC2,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,
∴S△ABC= AC BC=×3×4=6,
故答案为:6.
19.解:在Rt△AFC中,点D是AC的中点,AC=6cm,
∴DF=AC=×6=3(cm),
∵EF=1cm,
∴DE=DF+EF=3+1=4(cm),
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×4=8(cm),
故答案为:8cm.
20.解:∵D,E分别是△ABC的边AB和AC的中点,
∴DE是△ABC的中位线,
∵DE=4cm,
∴BC=2DE=8(cm).
故答案为:8.
21.解:如图,∵D、E、F分别是AB、BC、AC的中点,
∴DE=AC,DF=BC,EF=AB,
∴DE+DF+EF=AC+BC+AB,
∵△DEF∽△ABC,
∴所得到的△DEF与△ABC的周长之比是.
故答案为:.
22.解:延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠FAE,
∵AE⊥BE,
∴∠AEB=∠AEF=90°,
在△AEB和△AEF中,
,
∴△AEB≌△AEF(ASA),
∴AF=AB=3,BE=EF,
∴FC=AC﹣AF=5﹣3=2,
∵BD=DC,BE=EF,
∴DE=FC=1,
故答案为:1.
23.解:∵点D,点E分别是AB,AC边的中点,
∴DE是△ABC的中位线,
∴DE=BC=×6=3(cm),
故答案为:3.
24.解:∵D、E、F分别为AB、BC、AC的中点,
∴DE=AC,DF=BC,EF=AB,
∵△ABC的周长是2,
∴AB+AC+BC=2,
∴△DEF的周长=EF+DE+DF=×(AB+AC+BC)=1=2×,
同理可得:第三个三角形的周长=2×,
……
则第2021个三角形周长=2×=,
故答案为:.
25.解:∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半.
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16.
以此类推,第n个小三角形的周长是第一个三角形周长的64×()n﹣1=27﹣n
故答案是:27﹣n.
三.解答题
26.解:(1)由题意得:OC∥AD,
∵点C为AB的中点,
∴OC为△ABD的中位线,
∴OC=AD,
∵AD=1米,
∴OC=米;
(2)要把小聪最高翘到1.25米高,立柱OC的高度要升高为0.625米.
当AD=1.25米时,OC=0.625米,
所以要把小聪最高翘到1.25米高,立柱OC的高度要升高为0.625米.
27.证明:∵D,E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∵BD平分∠ABC,
∴∠CBD=∠EBD,
∵DE∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴DE=BE,
∵AB=2BE,
∴AB=2DE,
∴AB=BC,
∵点D是AC的中点,
∴BD⊥AC.
28.证明:∵AD=AC,AE⊥CD,
∴CE=ED,
∵F是BC的中点,
∴EF是△CDB的中位线,
∴BD=2EF.
29.(1)解:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,AB=6,CD=8,
∴PE∥AB,且PE=AB=3,PF∥CD且PF=CD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在直角△EPF中,由勾股定理得到:EF===5,
即EF=5;
(2)证明:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,
∴PE∥AB,且PE=AB,PF∥CD且PF=CD.
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°﹣∠BPF=180°﹣∠BDC,
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴PE2+PF2=(AB)2+(CD)2=EF2,
∴AB2+CD2=4EF2.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
