1.3 三视图学案(北师大版必修2)
文档属性
| 名称 | 1.3 三视图学案(北师大版必修2) |

|
|
| 格式 | zip | ||
| 文件大小 | 312.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-27 00:00:00 | ||
图片预览


文档简介
§3 三视图
自主学习
1.了解空间几何体的三视图的概念,初步认识简单几何体的三视图.
2.会画出空间几何体的三视图,并会由空间几何体的三视图画出空间几何体.
1.空间几何体的三视图是指__________、__________、__________.
2.三视图的主视图、俯视图、左视图分别是从正前方、正上方、左侧观察同一个几何体,画出空间几何体的图形.
3.三视图的排列规则是__________放在主视图的下方,长度与主视图一样,__________
放在主视图的右面,高度与主视图一样,宽度与俯视图的宽度一样.
对点讲练
简单几何体的三视图
例1 画出如图所示的正四棱锥的三视图.
点评 (1)在画三视图时,务必做到主(视图)左(视图)高平齐,主(视图)俯(视图)长对正,俯(视图)左(视图)宽相等.(2)习惯上将主视图与左视图画在同一水平位置上,俯视图在主视图的正下方.
变式训练1 画出如图所示的空间几何体的三视图(尺寸不作严格要求).
简单组合体的三视图
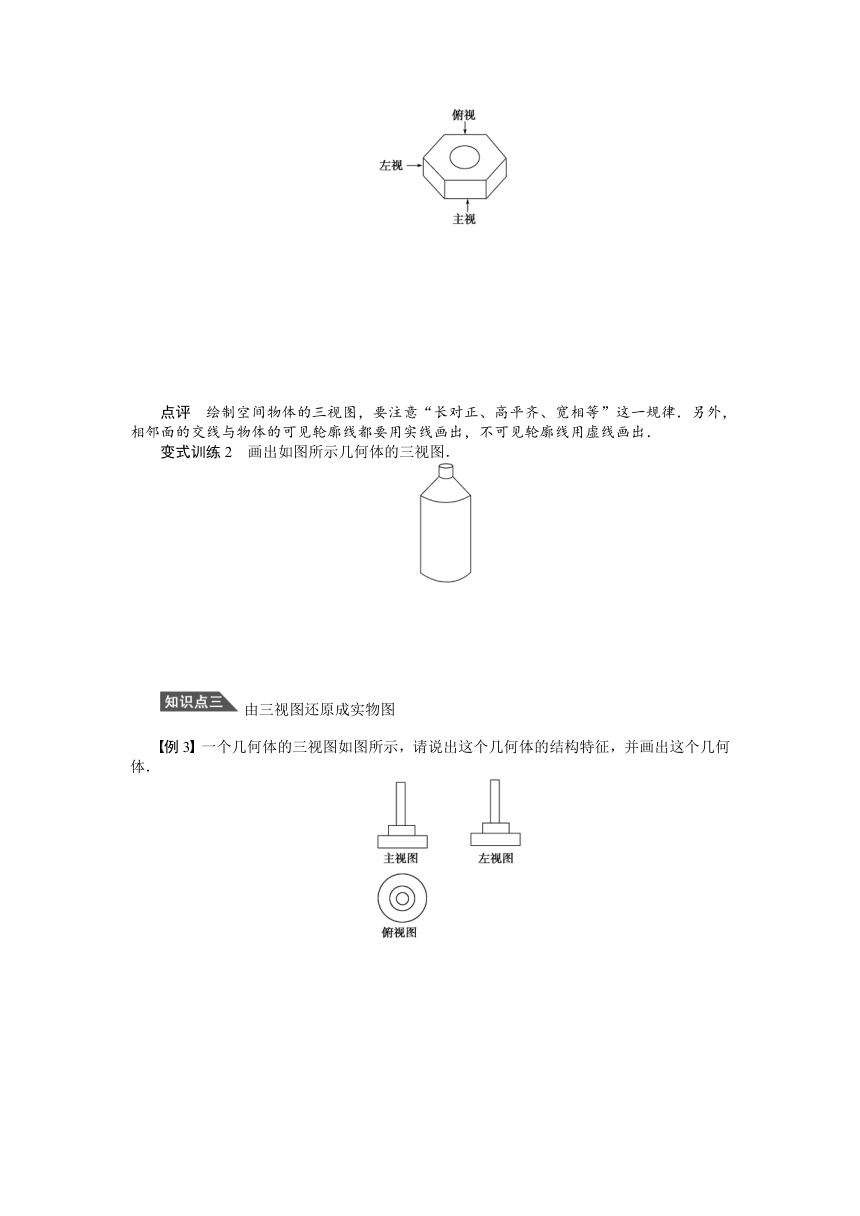
例2 画出螺母的三视图.
点评 绘制空间物体的三视图,要注意“长对正、高平齐、宽相等”这一规律.另外,相邻面的交线与物体的可见轮廓线都要用实线画出,不可见轮廓线用虚线画出.
变式训练2 画出如图所示几何体的三视图.
由三视图还原成实物图
例3 一个几何体的三视图如图所示,请说出这个几何体的结构特征,并画出这个几何体.
点评 只要熟悉简单几何体的三视图形式,由简单几何体的三视图还原几何体并不困难,对于组合体,需要综合主视图、左视图、俯视图的特征,确定分界线,找出组成组合体的简单几何体,再将组合体还原,其中确定分界线是正确还原的关键.
变式训练3 如图所示,根据三视图想像物体原形,并画出它的实物图.
在绘制三视图时,要掌握如下技巧:
(1)若两相邻物体的表面相交,表面的交线是它们的原分界线,在三视图中,分界线和可见轮廓线都用实线画出,不可见轮廓线用虚线画出;
(2)一个物体的三视图的排列规则是:俯视图放在主视图的下面,长度和主视图一样.左视图放在主视图的右面,高度和主视图一样,宽度和俯视图一样,简记为“长对正,高平齐,宽相等”;
(3)在画物体的三视图时应注意观察的角度,角度不同,往往画出的三视图不同.
课时作业
一、选择题
1.下列说法正确的是( )
A.任何几何体的三视图都与其摆放的位置有关
B.任何几何体的三视图都与其摆放的位置无关
C.有的几何体的三视图与其摆放的位置无关
D.正方体的三视图一定是三个全等的正方形
2.下列几何体的三视图中,三个视图不全相同的序号是( )
A.①② B.②③ C.③④ D.②④
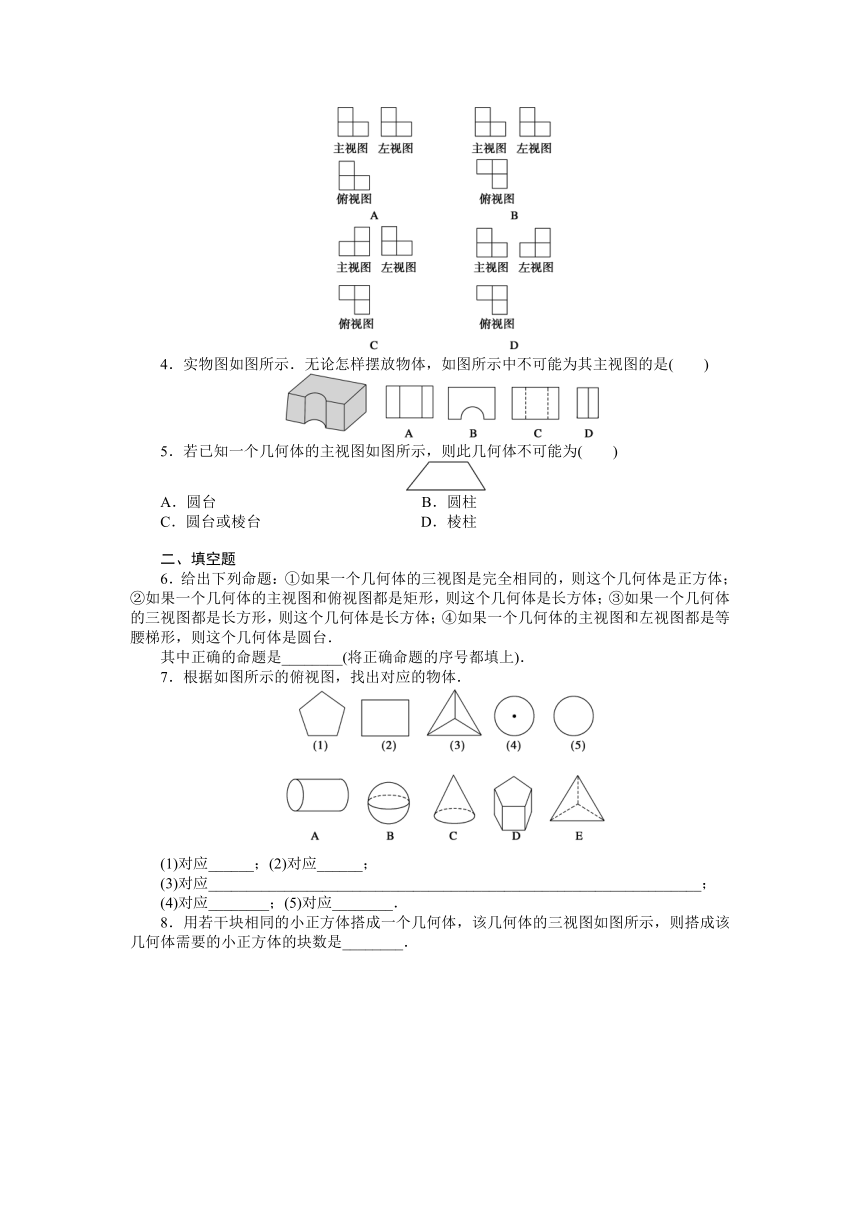
3.四个正方体按如图所示的方式放置,其中阴影部分为我们观察的正面,则该物体的三视图正确的为( )
4.实物图如图所示.无论怎样摆放物体,如图所示中不可能为其主视图的是( )
5.若已知一个几何体的主视图如图所示,则此几何体不可能为( )
A.圆台 B.圆柱
C.圆台或棱台 D.棱柱
二、填空题
6.给出下列命题:①如果一个几何体的三视图是完全相同的,则这个几何体是正方体;②如果一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;③如果一个几何体的三视图都是长方形,则这个几何体是长方体;④如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台.
其中正确的命题是________(将正确命题的序号都填上).
7.根据如图所示的俯视图,找出对应的物体.
(1)对应______;(2)对应______;
(3)对应_________________________________________________________________;
(4)对应________;(5)对应________.
8.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是________.
三、解答题
9.画出如图所示的几何体的三视图.
10.下图是一几何体的三视图,想象该几何体的几何结构特征,画出该几何体的形状.
§3 三视图 答案
自学导引
1.主视图 左视图 俯视图
3.俯视图 左视图
对点讲练
例1 解 正四棱锥的三视图如图所示:
变式训练1 解 三视图分别如图所示.
例2 解 三视图如图所示.
变式训练2 解 三视图如下图所示.
例3 解 由三视图可得几何体的直观图如图所示,该几何体是由三个圆柱拼接而成的组合体.
变式训练3 解
由三视图可以看出,该物体下部是一个长方体,上部是半个圆柱,在中间挖去了一个圆柱,虚线表示被挡住的轮廓线,实物图如图所示.
课时作业
1.C [球的三视图与其摆放位置无关.]
2.D [①的三个视图都是正方形,③的三个视图都是圆.]
3.B
4.D [A图可看做该物体槽向前时的主视图,B图可看做槽向下时的主视图,C图可看做槽向后时的主视图.]
5.B 6.③
7.(1)D (2)A (3)E (4)C (5)B
8.6
解析 由主视图和左视图,知该几何体由两层小正方体拼接成,由俯视图可知,最下层有5个小正方体,由左视图知上层仅有一个正方体,则共有6个小正方体.
9.解 三视图如图所示.
10.
解 由于俯视图有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合体,结合左视图和主视图,可知该几何体是由上面一个圆柱,
下面一个四棱柱拼接成的组合体.
该几何体的形状如图所示.
自主学习
1.了解空间几何体的三视图的概念,初步认识简单几何体的三视图.
2.会画出空间几何体的三视图,并会由空间几何体的三视图画出空间几何体.
1.空间几何体的三视图是指__________、__________、__________.
2.三视图的主视图、俯视图、左视图分别是从正前方、正上方、左侧观察同一个几何体,画出空间几何体的图形.
3.三视图的排列规则是__________放在主视图的下方,长度与主视图一样,__________
放在主视图的右面,高度与主视图一样,宽度与俯视图的宽度一样.
对点讲练
简单几何体的三视图
例1 画出如图所示的正四棱锥的三视图.
点评 (1)在画三视图时,务必做到主(视图)左(视图)高平齐,主(视图)俯(视图)长对正,俯(视图)左(视图)宽相等.(2)习惯上将主视图与左视图画在同一水平位置上,俯视图在主视图的正下方.
变式训练1 画出如图所示的空间几何体的三视图(尺寸不作严格要求).
简单组合体的三视图
例2 画出螺母的三视图.
点评 绘制空间物体的三视图,要注意“长对正、高平齐、宽相等”这一规律.另外,相邻面的交线与物体的可见轮廓线都要用实线画出,不可见轮廓线用虚线画出.
变式训练2 画出如图所示几何体的三视图.
由三视图还原成实物图
例3 一个几何体的三视图如图所示,请说出这个几何体的结构特征,并画出这个几何体.
点评 只要熟悉简单几何体的三视图形式,由简单几何体的三视图还原几何体并不困难,对于组合体,需要综合主视图、左视图、俯视图的特征,确定分界线,找出组成组合体的简单几何体,再将组合体还原,其中确定分界线是正确还原的关键.
变式训练3 如图所示,根据三视图想像物体原形,并画出它的实物图.
在绘制三视图时,要掌握如下技巧:
(1)若两相邻物体的表面相交,表面的交线是它们的原分界线,在三视图中,分界线和可见轮廓线都用实线画出,不可见轮廓线用虚线画出;
(2)一个物体的三视图的排列规则是:俯视图放在主视图的下面,长度和主视图一样.左视图放在主视图的右面,高度和主视图一样,宽度和俯视图一样,简记为“长对正,高平齐,宽相等”;
(3)在画物体的三视图时应注意观察的角度,角度不同,往往画出的三视图不同.
课时作业
一、选择题
1.下列说法正确的是( )
A.任何几何体的三视图都与其摆放的位置有关
B.任何几何体的三视图都与其摆放的位置无关
C.有的几何体的三视图与其摆放的位置无关
D.正方体的三视图一定是三个全等的正方形
2.下列几何体的三视图中,三个视图不全相同的序号是( )
A.①② B.②③ C.③④ D.②④
3.四个正方体按如图所示的方式放置,其中阴影部分为我们观察的正面,则该物体的三视图正确的为( )
4.实物图如图所示.无论怎样摆放物体,如图所示中不可能为其主视图的是( )
5.若已知一个几何体的主视图如图所示,则此几何体不可能为( )
A.圆台 B.圆柱
C.圆台或棱台 D.棱柱
二、填空题
6.给出下列命题:①如果一个几何体的三视图是完全相同的,则这个几何体是正方体;②如果一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;③如果一个几何体的三视图都是长方形,则这个几何体是长方体;④如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台.
其中正确的命题是________(将正确命题的序号都填上).
7.根据如图所示的俯视图,找出对应的物体.
(1)对应______;(2)对应______;
(3)对应_________________________________________________________________;
(4)对应________;(5)对应________.
8.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是________.
三、解答题
9.画出如图所示的几何体的三视图.
10.下图是一几何体的三视图,想象该几何体的几何结构特征,画出该几何体的形状.
§3 三视图 答案
自学导引
1.主视图 左视图 俯视图
3.俯视图 左视图
对点讲练
例1 解 正四棱锥的三视图如图所示:
变式训练1 解 三视图分别如图所示.
例2 解 三视图如图所示.
变式训练2 解 三视图如下图所示.
例3 解 由三视图可得几何体的直观图如图所示,该几何体是由三个圆柱拼接而成的组合体.
变式训练3 解
由三视图可以看出,该物体下部是一个长方体,上部是半个圆柱,在中间挖去了一个圆柱,虚线表示被挡住的轮廓线,实物图如图所示.
课时作业
1.C [球的三视图与其摆放位置无关.]
2.D [①的三个视图都是正方形,③的三个视图都是圆.]
3.B
4.D [A图可看做该物体槽向前时的主视图,B图可看做槽向下时的主视图,C图可看做槽向后时的主视图.]
5.B 6.③
7.(1)D (2)A (3)E (4)C (5)B
8.6
解析 由主视图和左视图,知该几何体由两层小正方体拼接成,由俯视图可知,最下层有5个小正方体,由左视图知上层仅有一个正方体,则共有6个小正方体.
9.解 三视图如图所示.
10.
解 由于俯视图有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合体,结合左视图和主视图,可知该几何体是由上面一个圆柱,
下面一个四棱柱拼接成的组合体.
该几何体的形状如图所示.
