鲁教版五四制九年级数学上册第三章 二次函数 达标检测卷(word版含答案)
文档属性
| 名称 | 鲁教版五四制九年级数学上册第三章 二次函数 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 354.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-13 08:56:47 | ||
图片预览




文档简介
第三章达标检测卷
一、选择题(每题3分,共30分)
1.下列函数中不属于二次函数的是( )
A.y=5x2 B.y=(x+1)2 C.y=2(x+2)2-2x2 D.y=1-x2
2.一个正方形的边长为5 cm,若边长减少x cm,则面积减少y cm2.下列说法正确的是( )
A.边长是自变量,面积减少量是因变量
B.边长是自变量,面积是因变量
C.y与x之间的函数关系式为y=(5-x)2
D.y与x之间的函数关系式为y=52-(5-x)2
3.抛物线y=-2(x-2)2-5的顶点坐标是( )
A.(-2,5) B.(2,5) C.(-2,-5) D.(2,-5)
4.抛物线y=x2-2是由抛物线y=x2( )
A.向下平移2个单位长度得到的 B.向上平移2个单位长度得到的
C.向左平移2个单位长度得到的 D.向右平移2个单位长度得到的
5.二次函数y=x2-2x-3的图象如图所示,当y<0时,自变量x的取值范围是( )
A.-1<x<3 B.x<-1
C.x>3 D.x<-1或x>3
6.点P1(-0.5,y1),P2(2.5,y2),P3(-5,y3)均在二次函数y=-x2+2x的图象上,则y1,y2,y3的大小关系是( )
A.y3>y2>y1 B.y3>y1=y2 C.y1>y2>y3 D.y1=y2>y3
7.已知某汽车刹车后行驶的距离y(单位:m)与行驶的时间t(单位:s)之间近似满足函数关系y=-6t2+15t,则该汽车刹车后到停下来所用的时间约为( )
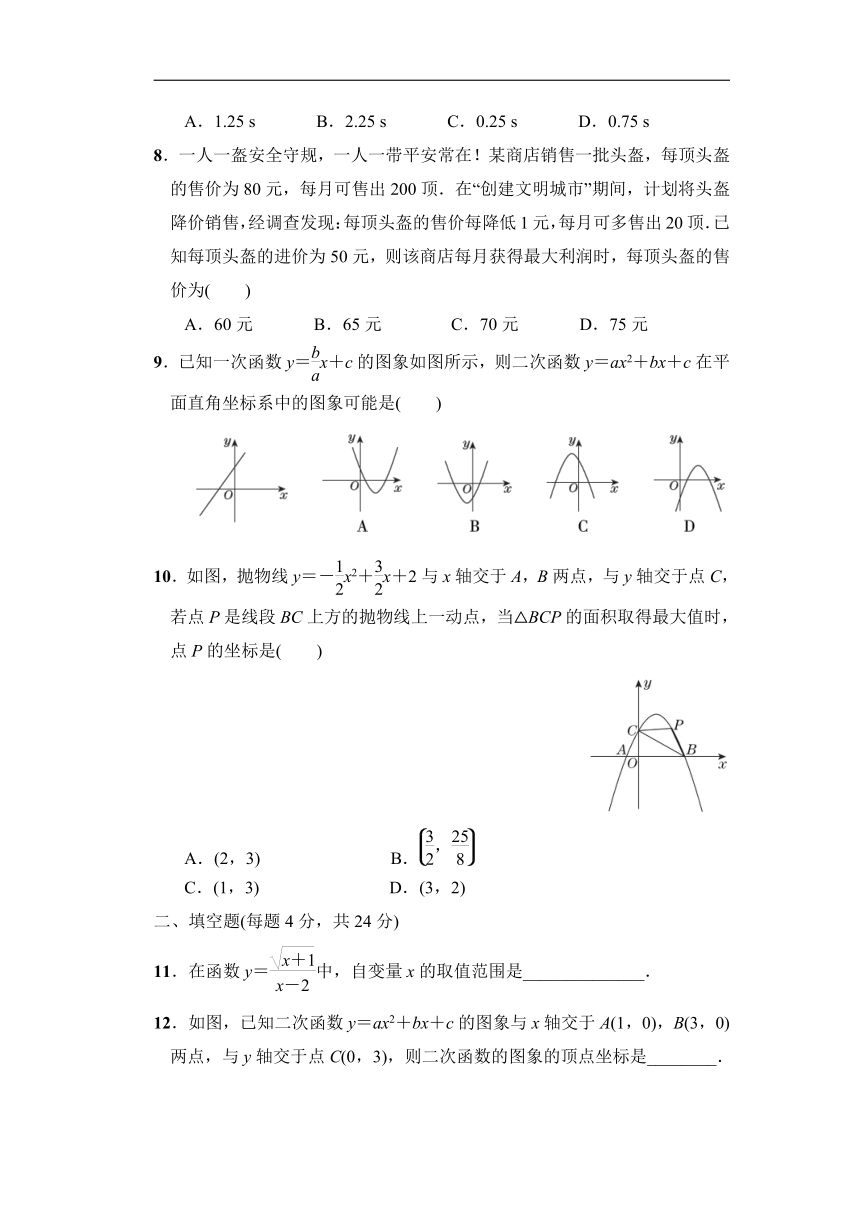
A.1.25 s B.2.25 s C.0.25 s D.0.75 s
8.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,每顶头盔的售价为80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每顶头盔的售价每降低1元,每月可多售出20顶.已知每顶头盔的进价为50元,则该商店每月获得最大利润时,每顶头盔的售价为( )
A.60元 B.65元 C.70元 D.75元
9.已知一次函数y=x+c的图象如图所示,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
10.如图,抛物线y=-x2+x+2与x轴交于A,B两点,与y轴交于点C,若点P是线段BC上方的抛物线上一动点,当△BCP的面积取得最大值时,点P的坐标是( )
A.(2,3) B.
C.(1,3) D.(3,2)
二、填空题(每题4分,共24分)
11.在函数y=中,自变量x的取值范围是______________.
12.如图,已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),则二次函数的图象的顶点坐标是________.
13.若函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为________.
14.从地面竖直向上抛出一小球,小球距地面的高度h(m)与小球的运动时间t(s)之间的函数关系如图所示.当h=30时,则t=________.
15.如图,抛物线y=-2x2+2与x轴交于点A,B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1,将C1向右平移得到C2,C2与x轴交于点B,D,C2的顶点为F,连接EF,则图中阴影部分的面积为________.
16.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A,B,顶点为C,对称轴为直线x=1,给出下列结论:①abc<0;②若点C的坐标为(1,2),则△ABC的面积可以等于2;③M(x1,y1),N(x2,y2)是抛物线上的两点(x1<x2),若x1+x2>2,则y1<y2; ④若抛物线经过点(3,-1),则方程ax2+bx+c+1=0的两根为-1,3.其中正确结论的序号有________.
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分,共66分)
17.已知二次函数的图象的顶点坐标为A(1,-4),且经过点B(3,0).
(1)求该二次函数的表达式;
(2)判断点C(2,-3)是否在该函数的图象上,并说明理由.
18.如图,抛物线y=x2+2与直线y=-x+4相交于B,C两点,抛物线、直线分别与y轴交于A,D两点.
(1)求点A,D的坐标;
(2)求△ABC的面积.
19.某产品每件的成本是120元,试销阶段,每件产品的销售价x(元)与产品的日销售量y(件)的部分对应值如下表,已知产品的日销售量y(件)是每件产品的销售价x(元)的一次函数,设每日获得的利润为P元.
x/元 130 150 165
y/件 70 50 35
(1)求y与x之间的函数关系式.
(2)求P与x之间的函数关系式.
(3)当每件产品的销售价为多少元时,才能使每日获得的利润最大?最大利润为多少?
20.已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的表达式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点?
21.如图,有一条双向公路隧道,其截面由抛物线和矩形的三边组成,隧道的最高点距地面4.9 m,AB=10 m,BC=2.4 m.现把隧道的截面放在直角坐标系中,若有一辆高为4 m、宽为2 m的装有集装箱的汽车要通过隧道,如果不考虑其他因素,汽车的右侧离隧道的右壁至少超过多少米,汽车才不会碰到隧道顶部?(抛物线部分为隧道顶部,AO,BC为石壁)
22.如图,在平面直角坐标系中,直线y=-2x-6与x轴交于点A,与y轴交于点B,抛物线y=x2+bx+c经过A,B两点.点P是位于直线AB下方抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点P到AB的距离最大时,求出点P的坐标;
(3)在(2)的条件下,连接BP,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,P,M,N为顶点,以BP为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.
答案
一、1.C 2.D 3.D 4.A 5.A 6.D
7.A 8.C 9.C
10.A 点拨:对于y=-x2+x+2,令y=0,则-x2+x+2=0,解得x=-1或x=4,令x=0,则y=2,∴点A,B,C的坐标分别为(-1,0),(4,0),(0,2),∴OB=4.
如图,过点P作y轴的平行线交BC于点H,
设直线BC的表达式为y=kx+b,将B(4,0),C(0,2)的坐标代入,得解得
∴直线BC的表达式为y=-x+2,
由题意设点P的坐标为,则点H的坐标为,
∴S△BCP=S△PHB+S△PHC=OB·
PH=×4×=-m2+4m=-(m-2)2+4,易知0<m<4,
∴当m=2时,△BCP的面积取得最大值,此时-m2+m+2=3,∴点P的坐标为(2,3).
二、11.x≥-1且x≠2 12.(2,-1)
13.0或2或-2 14.1.5或4.5 15.4
16.①④ 点拨:①∵抛物线的对称轴在y轴右侧,∴->0,∴a,b异号,即ab<0,∵抛物线与y轴的正半轴相交,
∴c>0,∴abc<0,故①正确;
②易知△ABC的面积=AB·yC,假设△ABC的面积为2,
∵C(1,2),∴AB×2=2,解得AB=2,设A(xA,0),B(xB,0),则AB=xB-xA=2.①
∵抛物线的对称轴为直线x=1,
∴xA+xB=2.②
由①②得,xA=0,xB=2,
∴A(0,0),此时c=0,与图象不符,故②错误;
③令x2>x1>1,此时x1+x2>2,
由图象知当x>1时,y随x的增大而减小,∴y1>y2,故③错误;
④抛物线y=ax2+bx+c向上平移1个单位长度可得抛物线
y=ax2+bx+c+1.
∵抛物线y=ax2+bx+c经过点(3,-1),对称轴为直线x=1,
∴抛物线y=ax2+bx+c+1经过点(3,0),对称轴为直线x=1,
∴抛物线y=ax2+bx+c+1也经过点(-1,0),
∴方程ax2+bx+c+1=0的两根为-1,3,故④正确.故答案为①④.
三、17.解:(1)设的表达式为y=a(x-h)2+k,
∵图象的顶点坐标为A(1,-4),∴y=a(x-1)2-4.
∵图象经过点B(3,0),
∴0=a(3-1)2-4,解得a=1,
∴该的表达式为y=(x-1)2-4=x2-2x-3.
(2)点C(2,-3)在该函数的图象上.
理由:当x=2时,y=22-2×2-3=-3,
∴点C在该函数的图象上.
18.解:(1)将x=0代入y=x2+2,
得y=2,∴点A的坐标为(0,2).
将x=0代入y=-x+4,得y=4,∴点D的坐标为(0,4).
(2)解
得或
∴点B的坐标为(1,3),点C的坐标为(-2,6),
由A(0,2),D(0,4),得AD=2,
∴S△ABC=S△ABD+S△ACD=×2×1+×2×2=3.
19.解:(1)设y与x之间的函数关系式为y=kx+b.
将x=130,y=70;x=150,y=50分别代入,得
解得∴y与x之间的函数关系式为y=-x+200.
(2)由题意知P=(x-120)(-x+200)=-x2+320x-24 000(120≤x≤200).
(3)∵P=-x2+320x-24 000=-(x-160)2+1 600,120≤x≤200,
∴当x=160时,P取最大值,为1 600.
∴当每件产品的销售价为160元时,才能使每日获得的利润最大,最大利润为1 600元.
20.(1)证明:∵y=(x-m)2-(x-m)=x2-(2m+1)x+m2+m,
∴Δ=[-(2m+1)]2-4(m2+m)=1>0,∴不论m为何值,该抛物线与x轴一定有两个公共点.
(2)解:①由(1)知抛物线的对称轴为直线x=-=,
∴m=2,∴该抛物线的表达式为y=x2-5x+6.
②设把该抛物线沿y轴向上平移k个单位长度,则平移后抛物线的表达式为y=x2-5x+6+k,
∵抛物线y=x2-5x+6+k与x轴只有一个公共点,∴Δ=(-5)2-4(6+k)=0,∴k=,
∴把该抛物线沿y轴向上平移个单位长度后,得到的抛物线与x轴只有一个公共点.
21.解:由题意得抛物线的顶点坐标为(5,2.5),且过点C(10,0),易求出抛物线的函数表达式为y=-x2+x.如图,用矩形DEFG表示汽车的截面,设BD=m,DG交x轴于M,延长DG交抛物线于H,则AD=(10-m)m,∴HM=m.
∴HD=m.
由题意得-(10-m)2+12.4-m>4,化简得(m-2)(m-8)<0,∴2<m<8.
易知m≤3,
∴2<m≤3.
答:汽车的右侧离隧道右壁至少超过2 m,汽车才不会碰到隧道顶部.
22.解:(1)对于y=-2x-6,令x=0,得y=-6,令y=0,得x=-3,
∴A(-3,0),B(0,-6),
把A(-3,0),B(0,-6)的坐标分别代入y=x2+bx+c,
得解得
∴抛物线的表达式为y=x2+x-6.
(2)如图,过点P作PH⊥AB于点H,PD⊥x轴于点D,交AB于点Q,则∠ADQ=∠PHQ=90°.
∴∠PQH=∠AQD=90°-∠DAQ,
∵∠AOB=90°,
∴∠ABO=90°-∠DAQ,
∴∠PQH=∠ABO.
又∵∠PHQ=∠AOB=90°,
∴△PHQ∽△AOB,
∴=,
∵A(-3,0),B(0,-6),
∴OA=3,OB=6,
∴AB==3 .
∴=,
∴PH=PQ,
∴当PQ最大时,PH最大.
设P(t,t2+t-6),则Q(t,-2t-6),
∴PQ=(-2t-6)-(t2+t-6)=-t2-3t=-+,
易知-3<t<0,
∴当t=-时,PQ取得最大值,此时PH最大.
当t=-时,t2+t-6=-,
∴点P的坐标为.
(3)存在,由题意知点M的纵坐标为0.设N(n,n2+n-6),由(1)(2)知B(0,-6),P.
①若平行四边形的对角线为MB,NP,
则MB的中点也是NP的中点,
∴0-6=n2+n-6-,
解得n=或n=,
∴点N的坐标为
或 .
②若平行四边形的对角线为MP,NB,则MP的中点也是NB的中点,
∴0-=n2+n-6-6,
解得n=或n=,
∴点N的坐标为
或.
综上所述,点N的坐标为或
或
或
.
一、选择题(每题3分,共30分)
1.下列函数中不属于二次函数的是( )
A.y=5x2 B.y=(x+1)2 C.y=2(x+2)2-2x2 D.y=1-x2
2.一个正方形的边长为5 cm,若边长减少x cm,则面积减少y cm2.下列说法正确的是( )
A.边长是自变量,面积减少量是因变量
B.边长是自变量,面积是因变量
C.y与x之间的函数关系式为y=(5-x)2
D.y与x之间的函数关系式为y=52-(5-x)2
3.抛物线y=-2(x-2)2-5的顶点坐标是( )
A.(-2,5) B.(2,5) C.(-2,-5) D.(2,-5)
4.抛物线y=x2-2是由抛物线y=x2( )
A.向下平移2个单位长度得到的 B.向上平移2个单位长度得到的
C.向左平移2个单位长度得到的 D.向右平移2个单位长度得到的
5.二次函数y=x2-2x-3的图象如图所示,当y<0时,自变量x的取值范围是( )
A.-1<x<3 B.x<-1
C.x>3 D.x<-1或x>3
6.点P1(-0.5,y1),P2(2.5,y2),P3(-5,y3)均在二次函数y=-x2+2x的图象上,则y1,y2,y3的大小关系是( )
A.y3>y2>y1 B.y3>y1=y2 C.y1>y2>y3 D.y1=y2>y3
7.已知某汽车刹车后行驶的距离y(单位:m)与行驶的时间t(单位:s)之间近似满足函数关系y=-6t2+15t,则该汽车刹车后到停下来所用的时间约为( )
A.1.25 s B.2.25 s C.0.25 s D.0.75 s
8.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,每顶头盔的售价为80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每顶头盔的售价每降低1元,每月可多售出20顶.已知每顶头盔的进价为50元,则该商店每月获得最大利润时,每顶头盔的售价为( )
A.60元 B.65元 C.70元 D.75元
9.已知一次函数y=x+c的图象如图所示,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
10.如图,抛物线y=-x2+x+2与x轴交于A,B两点,与y轴交于点C,若点P是线段BC上方的抛物线上一动点,当△BCP的面积取得最大值时,点P的坐标是( )
A.(2,3) B.
C.(1,3) D.(3,2)
二、填空题(每题4分,共24分)
11.在函数y=中,自变量x的取值范围是______________.
12.如图,已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),则二次函数的图象的顶点坐标是________.
13.若函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为________.
14.从地面竖直向上抛出一小球,小球距地面的高度h(m)与小球的运动时间t(s)之间的函数关系如图所示.当h=30时,则t=________.
15.如图,抛物线y=-2x2+2与x轴交于点A,B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1,将C1向右平移得到C2,C2与x轴交于点B,D,C2的顶点为F,连接EF,则图中阴影部分的面积为________.
16.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A,B,顶点为C,对称轴为直线x=1,给出下列结论:①abc<0;②若点C的坐标为(1,2),则△ABC的面积可以等于2;③M(x1,y1),N(x2,y2)是抛物线上的两点(x1<x2),若x1+x2>2,则y1<y2; ④若抛物线经过点(3,-1),则方程ax2+bx+c+1=0的两根为-1,3.其中正确结论的序号有________.
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分,共66分)
17.已知二次函数的图象的顶点坐标为A(1,-4),且经过点B(3,0).
(1)求该二次函数的表达式;
(2)判断点C(2,-3)是否在该函数的图象上,并说明理由.
18.如图,抛物线y=x2+2与直线y=-x+4相交于B,C两点,抛物线、直线分别与y轴交于A,D两点.
(1)求点A,D的坐标;
(2)求△ABC的面积.
19.某产品每件的成本是120元,试销阶段,每件产品的销售价x(元)与产品的日销售量y(件)的部分对应值如下表,已知产品的日销售量y(件)是每件产品的销售价x(元)的一次函数,设每日获得的利润为P元.
x/元 130 150 165
y/件 70 50 35
(1)求y与x之间的函数关系式.
(2)求P与x之间的函数关系式.
(3)当每件产品的销售价为多少元时,才能使每日获得的利润最大?最大利润为多少?
20.已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的表达式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点?
21.如图,有一条双向公路隧道,其截面由抛物线和矩形的三边组成,隧道的最高点距地面4.9 m,AB=10 m,BC=2.4 m.现把隧道的截面放在直角坐标系中,若有一辆高为4 m、宽为2 m的装有集装箱的汽车要通过隧道,如果不考虑其他因素,汽车的右侧离隧道的右壁至少超过多少米,汽车才不会碰到隧道顶部?(抛物线部分为隧道顶部,AO,BC为石壁)
22.如图,在平面直角坐标系中,直线y=-2x-6与x轴交于点A,与y轴交于点B,抛物线y=x2+bx+c经过A,B两点.点P是位于直线AB下方抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点P到AB的距离最大时,求出点P的坐标;
(3)在(2)的条件下,连接BP,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,P,M,N为顶点,以BP为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.
答案
一、1.C 2.D 3.D 4.A 5.A 6.D
7.A 8.C 9.C
10.A 点拨:对于y=-x2+x+2,令y=0,则-x2+x+2=0,解得x=-1或x=4,令x=0,则y=2,∴点A,B,C的坐标分别为(-1,0),(4,0),(0,2),∴OB=4.
如图,过点P作y轴的平行线交BC于点H,
设直线BC的表达式为y=kx+b,将B(4,0),C(0,2)的坐标代入,得解得
∴直线BC的表达式为y=-x+2,
由题意设点P的坐标为,则点H的坐标为,
∴S△BCP=S△PHB+S△PHC=OB·
PH=×4×=-m2+4m=-(m-2)2+4,易知0<m<4,
∴当m=2时,△BCP的面积取得最大值,此时-m2+m+2=3,∴点P的坐标为(2,3).
二、11.x≥-1且x≠2 12.(2,-1)
13.0或2或-2 14.1.5或4.5 15.4
16.①④ 点拨:①∵抛物线的对称轴在y轴右侧,∴->0,∴a,b异号,即ab<0,∵抛物线与y轴的正半轴相交,
∴c>0,∴abc<0,故①正确;
②易知△ABC的面积=AB·yC,假设△ABC的面积为2,
∵C(1,2),∴AB×2=2,解得AB=2,设A(xA,0),B(xB,0),则AB=xB-xA=2.①
∵抛物线的对称轴为直线x=1,
∴xA+xB=2.②
由①②得,xA=0,xB=2,
∴A(0,0),此时c=0,与图象不符,故②错误;
③令x2>x1>1,此时x1+x2>2,
由图象知当x>1时,y随x的增大而减小,∴y1>y2,故③错误;
④抛物线y=ax2+bx+c向上平移1个单位长度可得抛物线
y=ax2+bx+c+1.
∵抛物线y=ax2+bx+c经过点(3,-1),对称轴为直线x=1,
∴抛物线y=ax2+bx+c+1经过点(3,0),对称轴为直线x=1,
∴抛物线y=ax2+bx+c+1也经过点(-1,0),
∴方程ax2+bx+c+1=0的两根为-1,3,故④正确.故答案为①④.
三、17.解:(1)设的表达式为y=a(x-h)2+k,
∵图象的顶点坐标为A(1,-4),∴y=a(x-1)2-4.
∵图象经过点B(3,0),
∴0=a(3-1)2-4,解得a=1,
∴该的表达式为y=(x-1)2-4=x2-2x-3.
(2)点C(2,-3)在该函数的图象上.
理由:当x=2时,y=22-2×2-3=-3,
∴点C在该函数的图象上.
18.解:(1)将x=0代入y=x2+2,
得y=2,∴点A的坐标为(0,2).
将x=0代入y=-x+4,得y=4,∴点D的坐标为(0,4).
(2)解
得或
∴点B的坐标为(1,3),点C的坐标为(-2,6),
由A(0,2),D(0,4),得AD=2,
∴S△ABC=S△ABD+S△ACD=×2×1+×2×2=3.
19.解:(1)设y与x之间的函数关系式为y=kx+b.
将x=130,y=70;x=150,y=50分别代入,得
解得∴y与x之间的函数关系式为y=-x+200.
(2)由题意知P=(x-120)(-x+200)=-x2+320x-24 000(120≤x≤200).
(3)∵P=-x2+320x-24 000=-(x-160)2+1 600,120≤x≤200,
∴当x=160时,P取最大值,为1 600.
∴当每件产品的销售价为160元时,才能使每日获得的利润最大,最大利润为1 600元.
20.(1)证明:∵y=(x-m)2-(x-m)=x2-(2m+1)x+m2+m,
∴Δ=[-(2m+1)]2-4(m2+m)=1>0,∴不论m为何值,该抛物线与x轴一定有两个公共点.
(2)解:①由(1)知抛物线的对称轴为直线x=-=,
∴m=2,∴该抛物线的表达式为y=x2-5x+6.
②设把该抛物线沿y轴向上平移k个单位长度,则平移后抛物线的表达式为y=x2-5x+6+k,
∵抛物线y=x2-5x+6+k与x轴只有一个公共点,∴Δ=(-5)2-4(6+k)=0,∴k=,
∴把该抛物线沿y轴向上平移个单位长度后,得到的抛物线与x轴只有一个公共点.
21.解:由题意得抛物线的顶点坐标为(5,2.5),且过点C(10,0),易求出抛物线的函数表达式为y=-x2+x.如图,用矩形DEFG表示汽车的截面,设BD=m,DG交x轴于M,延长DG交抛物线于H,则AD=(10-m)m,∴HM=m.
∴HD=m.
由题意得-(10-m)2+12.4-m>4,化简得(m-2)(m-8)<0,∴2<m<8.
易知m≤3,
∴2<m≤3.
答:汽车的右侧离隧道右壁至少超过2 m,汽车才不会碰到隧道顶部.
22.解:(1)对于y=-2x-6,令x=0,得y=-6,令y=0,得x=-3,
∴A(-3,0),B(0,-6),
把A(-3,0),B(0,-6)的坐标分别代入y=x2+bx+c,
得解得
∴抛物线的表达式为y=x2+x-6.
(2)如图,过点P作PH⊥AB于点H,PD⊥x轴于点D,交AB于点Q,则∠ADQ=∠PHQ=90°.
∴∠PQH=∠AQD=90°-∠DAQ,
∵∠AOB=90°,
∴∠ABO=90°-∠DAQ,
∴∠PQH=∠ABO.
又∵∠PHQ=∠AOB=90°,
∴△PHQ∽△AOB,
∴=,
∵A(-3,0),B(0,-6),
∴OA=3,OB=6,
∴AB==3 .
∴=,
∴PH=PQ,
∴当PQ最大时,PH最大.
设P(t,t2+t-6),则Q(t,-2t-6),
∴PQ=(-2t-6)-(t2+t-6)=-t2-3t=-+,
易知-3<t<0,
∴当t=-时,PQ取得最大值,此时PH最大.
当t=-时,t2+t-6=-,
∴点P的坐标为.
(3)存在,由题意知点M的纵坐标为0.设N(n,n2+n-6),由(1)(2)知B(0,-6),P.
①若平行四边形的对角线为MB,NP,
则MB的中点也是NP的中点,
∴0-6=n2+n-6-,
解得n=或n=,
∴点N的坐标为
或 .
②若平行四边形的对角线为MP,NB,则MP的中点也是NB的中点,
∴0-=n2+n-6-6,
解得n=或n=,
∴点N的坐标为
或.
综上所述,点N的坐标为或
或
或
.
