2021-2022学年鲁教版(五四制)数学九年级上册 第四章 投影与视图 达标检测卷(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)数学九年级上册 第四章 投影与视图 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-13 09:33:08 | ||
图片预览


文档简介
第四章达标检测卷
(120分,90分钟)
一、选择题(每题3分,共30分)
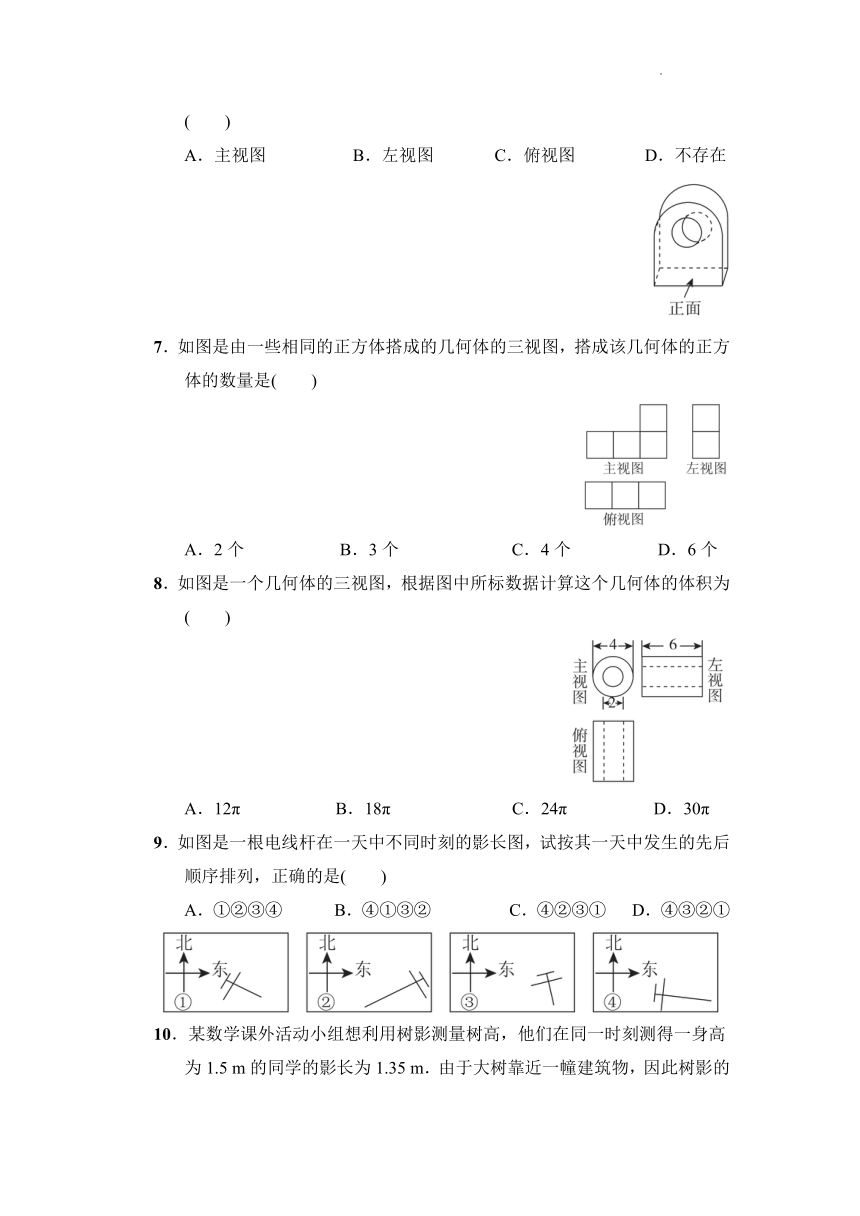
1.如图,该几何体的俯视图是( )
A.正方形 B.长方形 C.三角形 D.圆
2.下列各种现象属于中心投影的是( )
A.晚上人走在路灯下的影子 B.中午用来乘凉的树影
C.上午人走在路上的影子 D.早上升旗时地面上旗杆的影子
3.如图是某个几何体的三视图,该几何体是( )
A.三棱柱 B.三棱锥 C.四棱锥 D.四棱柱
4.圆形的物体在太阳光照射下的投影的形状是( )
A.圆 B.椭圆 C.线段 D.以上都有可能
5.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30 cm,光源到屏幕的距离为90 cm,且幻灯片上的图形的高度为7 cm,则屏幕上图形的高度为( )
A.21 cm B.14 cm C.6 cm D.24 cm
6.如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( )
A.主视图 B.左视图 C.俯视图 D.不存在
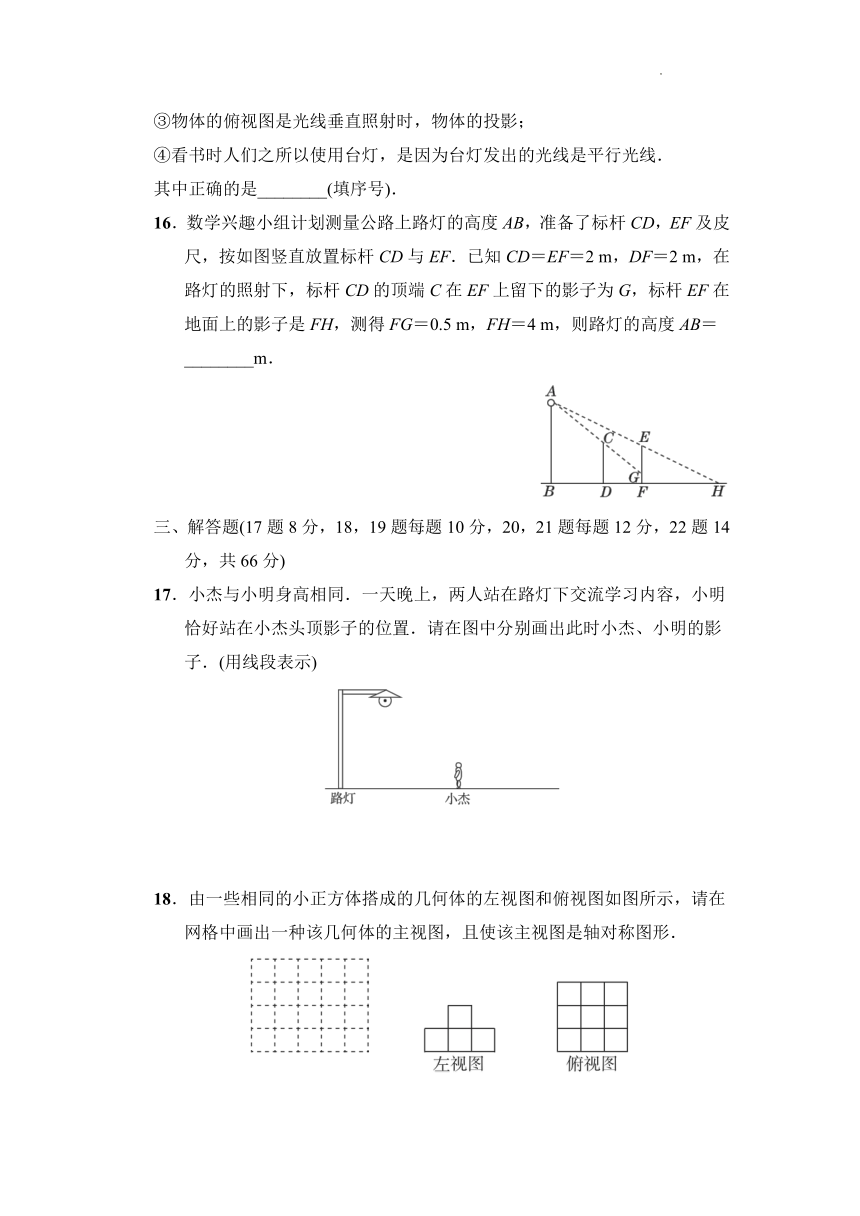
7.如图是由一些相同的正方体搭成的几何体的三视图,搭成该几何体的正方体的数量是( )
A.2个 B.3个 C.4个 D.6个
8.如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( )
A.12π B.18π C.24π D.30π
9.如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
10.某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5 m的同学的影长为1.35 m.由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6 m,建筑物上的影长为1.8 m,则树的高度为( )
A.5.4 m B.5.8 m C.5.22 m D.6.4 m
二、填空题(每题4分,共24分)
11.在桌面上放置以下几何体:①圆柱;②正方体;③球.其中,主视图与左视图可能不同的是__________(填序号).
12.某学校操场上立着高度不同的甲、乙两种篮球架,那么在某一时刻的太阳光的照射下,甲种篮球架的高度与其影长的比________(填“大于”“小于”或“等于”)乙种篮球架的高度与其影长的比.
13.一个长方体的主视图和俯视图如图所示,则这个长方体左视图的面积为______cm2.
14.如图是由几个相同的小正方体搭成的几何体,在保持主视图和左视图不变的情况下,最多可以拿掉________个小正方体.
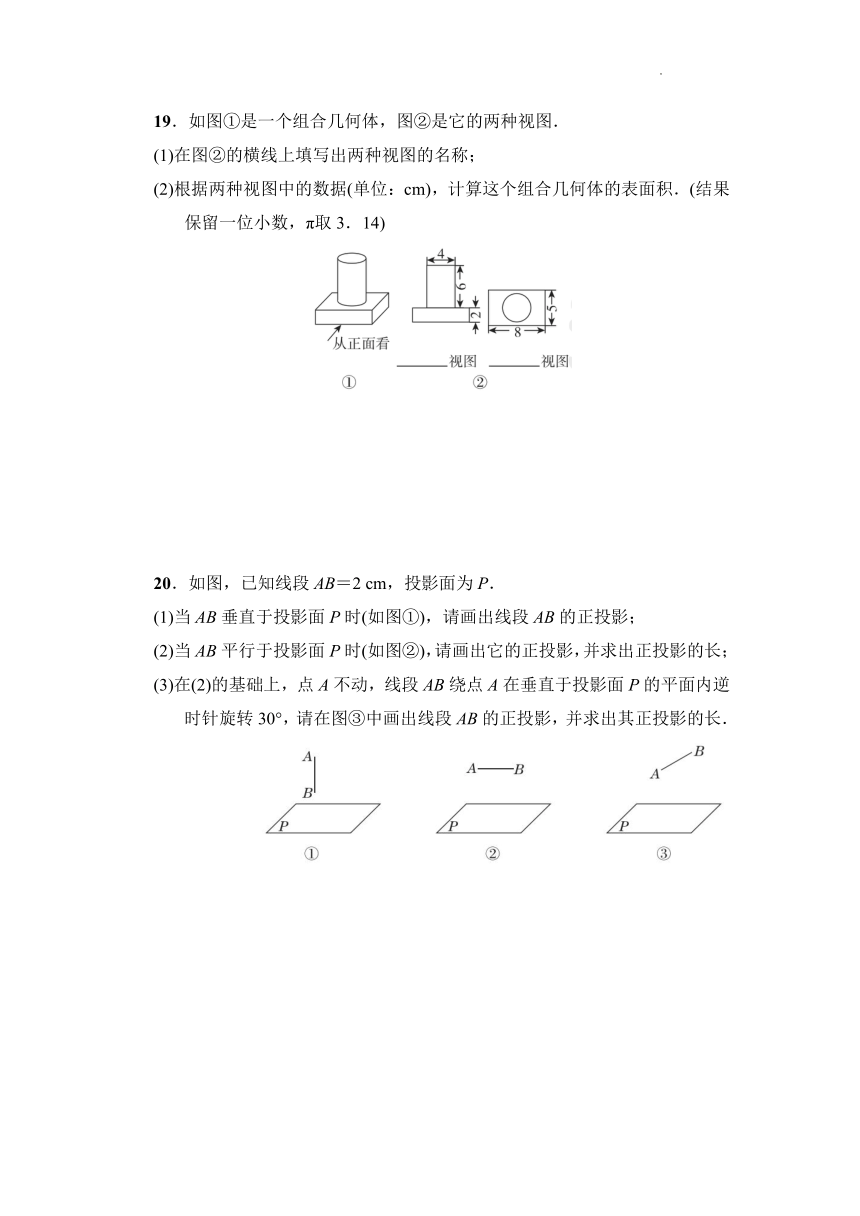
15.对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;
③物体的俯视图是光线垂直照射时,物体的投影;
④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.
其中正确的是________(填序号).
16.数学兴趣小组计划测量公路上路灯的高度AB,准备了标杆CD,EF及皮尺,按如图竖直放置标杆CD与EF.已知CD=EF=2 m,DF=2 m,在路灯的照射下,标杆CD的顶端C在EF上留下的影子为G,标杆EF在地面上的影子是FH,测得FG=0.5 m,FH=4 m,则路灯的高度AB=________m.
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分,共66分)
17.小杰与小明身高相同.一天晚上,两人站在路灯下交流学习内容,小明恰好站在小杰头顶影子的位置.请在图中分别画出此时小杰、小明的影子.(用线段表示)
18.由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中画出一种该几何体的主视图,且使该主视图是轴对称图形.
19.如图①是一个组合几何体,图②是它的两种视图.
(1)在图②的横线上填写出两种视图的名称;
(2)根据两种视图中的数据(单位:cm),计算这个组合几何体的表面积.(结果保留一位小数,π取3.14)
20.如图,已知线段AB=2 cm,投影面为P.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的正投影;
(2)当AB平行于投影面P时(如图②),请画出它的正投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图③中画出线段AB的正投影,并求出其正投影的长.
21.如图,九(1)班的小明与小艳两名同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画法;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
22.为加快新农村建设,某市投入资金建设新型农村社区.如图为住宅区内的两幢楼,它们的高AB=CD=30 m,现需了解甲楼对乙楼采光情况的影响.当太阳光线与水平线的夹角为30°时,试求:
(1)若两楼间的距离AC=24 m,则甲楼落在乙楼上的影子有多高;(结果保留根号)
(2)若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当有多远.(结果保留根号)
答案
一、1.C 2.A 3.C 4.D 5.A 6.C
7.C 8.B 9.B 10.B
二、11. ① 12.等于 13.6 14.1 15.①
16.5 点拨:如图,延长CG交FH于点M.
∵∠GMF=∠CMD,∠GFM=∠CDM=90°,∴△GFM∽△CDM.
∴=,即=,
解得FM= m.
设BD=x m,AB=y m,
易得△AMB∽△CMD,△ABH∽△EFH,∴=,=,
可得
解得∴AB=5 m.
三、17.解:如图,小杰、小明的影子分别为线段EF、线段DF.
18.解:如图所示.
19.解:(1)主;俯
(2)这个组合几何体的表面积为: 2×(8×5+8×2+5×2)+4×π×6≈132+4×3.14×6≈207.4(cm2).
20.解:(1)画图略.
(2)画图略.
线段AB的正投影的长为2 cm.
(3)画图略.
线段AB的正投影的长为2cos 30°=2×=(cm).
21.解:(1)如图,线段EF就是此时旗杆DE在阳光下的投影.
画法:连接AC,过点D作DF∥AC,交直线BE于点F,则线段EF即为所求.
(2)∵AC∥DF,∴∠ACB=∠DFE.
又∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF.∴=.
∵AB=3 m,BC=2 m,EF=6 m,
∴=.
∴DE=9 m,即旗杆DE的高度为9 m.
22.解:(1)由AB=CD=30 m,AB⊥AC,CD⊥AC,易得四边形ABDC是矩形.
∴BD=AC=24 m,∠BDE=90°.
∵∠DBE=30°,
∴DE=BD·tan ∠DBE=24×tan 30°=24×=8 (m).
∴EC=CD-DE=(30-8 )m,
即甲楼落在乙楼上的影子有(30-8 )m高.
(2)如图.当太阳光照射到点C时,甲楼的影子刚好不影响乙楼.
在Rt△ABC中,AB=30 m,∠ACB=30°,
∴AC===30×=30 (m).
∴若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当有30 m远.
1
(120分,90分钟)
一、选择题(每题3分,共30分)
1.如图,该几何体的俯视图是( )
A.正方形 B.长方形 C.三角形 D.圆
2.下列各种现象属于中心投影的是( )
A.晚上人走在路灯下的影子 B.中午用来乘凉的树影
C.上午人走在路上的影子 D.早上升旗时地面上旗杆的影子
3.如图是某个几何体的三视图,该几何体是( )
A.三棱柱 B.三棱锥 C.四棱锥 D.四棱柱
4.圆形的物体在太阳光照射下的投影的形状是( )
A.圆 B.椭圆 C.线段 D.以上都有可能
5.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30 cm,光源到屏幕的距离为90 cm,且幻灯片上的图形的高度为7 cm,则屏幕上图形的高度为( )
A.21 cm B.14 cm C.6 cm D.24 cm
6.如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( )
A.主视图 B.左视图 C.俯视图 D.不存在
7.如图是由一些相同的正方体搭成的几何体的三视图,搭成该几何体的正方体的数量是( )
A.2个 B.3个 C.4个 D.6个
8.如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( )
A.12π B.18π C.24π D.30π
9.如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
10.某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5 m的同学的影长为1.35 m.由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6 m,建筑物上的影长为1.8 m,则树的高度为( )
A.5.4 m B.5.8 m C.5.22 m D.6.4 m
二、填空题(每题4分,共24分)
11.在桌面上放置以下几何体:①圆柱;②正方体;③球.其中,主视图与左视图可能不同的是__________(填序号).
12.某学校操场上立着高度不同的甲、乙两种篮球架,那么在某一时刻的太阳光的照射下,甲种篮球架的高度与其影长的比________(填“大于”“小于”或“等于”)乙种篮球架的高度与其影长的比.
13.一个长方体的主视图和俯视图如图所示,则这个长方体左视图的面积为______cm2.
14.如图是由几个相同的小正方体搭成的几何体,在保持主视图和左视图不变的情况下,最多可以拿掉________个小正方体.
15.对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;
③物体的俯视图是光线垂直照射时,物体的投影;
④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.
其中正确的是________(填序号).
16.数学兴趣小组计划测量公路上路灯的高度AB,准备了标杆CD,EF及皮尺,按如图竖直放置标杆CD与EF.已知CD=EF=2 m,DF=2 m,在路灯的照射下,标杆CD的顶端C在EF上留下的影子为G,标杆EF在地面上的影子是FH,测得FG=0.5 m,FH=4 m,则路灯的高度AB=________m.
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分,共66分)
17.小杰与小明身高相同.一天晚上,两人站在路灯下交流学习内容,小明恰好站在小杰头顶影子的位置.请在图中分别画出此时小杰、小明的影子.(用线段表示)
18.由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中画出一种该几何体的主视图,且使该主视图是轴对称图形.
19.如图①是一个组合几何体,图②是它的两种视图.
(1)在图②的横线上填写出两种视图的名称;
(2)根据两种视图中的数据(单位:cm),计算这个组合几何体的表面积.(结果保留一位小数,π取3.14)
20.如图,已知线段AB=2 cm,投影面为P.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的正投影;
(2)当AB平行于投影面P时(如图②),请画出它的正投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图③中画出线段AB的正投影,并求出其正投影的长.
21.如图,九(1)班的小明与小艳两名同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画法;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
22.为加快新农村建设,某市投入资金建设新型农村社区.如图为住宅区内的两幢楼,它们的高AB=CD=30 m,现需了解甲楼对乙楼采光情况的影响.当太阳光线与水平线的夹角为30°时,试求:
(1)若两楼间的距离AC=24 m,则甲楼落在乙楼上的影子有多高;(结果保留根号)
(2)若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当有多远.(结果保留根号)
答案
一、1.C 2.A 3.C 4.D 5.A 6.C
7.C 8.B 9.B 10.B
二、11. ① 12.等于 13.6 14.1 15.①
16.5 点拨:如图,延长CG交FH于点M.
∵∠GMF=∠CMD,∠GFM=∠CDM=90°,∴△GFM∽△CDM.
∴=,即=,
解得FM= m.
设BD=x m,AB=y m,
易得△AMB∽△CMD,△ABH∽△EFH,∴=,=,
可得
解得∴AB=5 m.
三、17.解:如图,小杰、小明的影子分别为线段EF、线段DF.
18.解:如图所示.
19.解:(1)主;俯
(2)这个组合几何体的表面积为: 2×(8×5+8×2+5×2)+4×π×6≈132+4×3.14×6≈207.4(cm2).
20.解:(1)画图略.
(2)画图略.
线段AB的正投影的长为2 cm.
(3)画图略.
线段AB的正投影的长为2cos 30°=2×=(cm).
21.解:(1)如图,线段EF就是此时旗杆DE在阳光下的投影.
画法:连接AC,过点D作DF∥AC,交直线BE于点F,则线段EF即为所求.
(2)∵AC∥DF,∴∠ACB=∠DFE.
又∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF.∴=.
∵AB=3 m,BC=2 m,EF=6 m,
∴=.
∴DE=9 m,即旗杆DE的高度为9 m.
22.解:(1)由AB=CD=30 m,AB⊥AC,CD⊥AC,易得四边形ABDC是矩形.
∴BD=AC=24 m,∠BDE=90°.
∵∠DBE=30°,
∴DE=BD·tan ∠DBE=24×tan 30°=24×=8 (m).
∴EC=CD-DE=(30-8 )m,
即甲楼落在乙楼上的影子有(30-8 )m高.
(2)如图.当太阳光照射到点C时,甲楼的影子刚好不影响乙楼.
在Rt△ABC中,AB=30 m,∠ACB=30°,
∴AC===30×=30 (m).
∴若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当有30 m远.
1
