2021-2022学年上海市徐汇区重点中学九年级(下)摸底数学试卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年上海市徐汇区重点中学九年级(下)摸底数学试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-13 08:44:09 | ||
图片预览


文档简介
2021-2022学年上海市徐汇区重点中学九年级(下)摸底数学试卷
一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.下列属于单项式的是( )
A.a+b B. C. D.1
2.下列运算中,正确的是( )
A.2x4﹣3x2=﹣x2 B.2x4+3x2=5x6
C.2x4 3x2=6x8 D.2x4 3x2=6x6
3.已知A(1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m>﹣ D.m<﹣
4.某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )
年龄(单位:岁) 14 15 16 17 18
人数 3 3 5 3 2
A.16,17 B.16,16 C.16,16.5 D.3,17
5.下列命题中,假命题是( )
A.对角线垂直的平行四边形是菱形
B.对角线互相平分且垂直的四边形是菱形
C.对角线互相平分且平分一组内角的四边形是菱形
D.对角线相等且垂直的四边形是菱形
6.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,DE∥BC,且AD=2CD,则以点C为圆心、DC长为半径的圆C和以点E为圆心、EB长为半径的圆E的位置关系是( )
A.外离 B.相交 C.外切 D.不能确定
二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置]
7.数据384400用科学记数法表示为 .
8.化简:= .
9.若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是 .
10.方程=3的解是 .
11.方程x2﹣=3x﹣4中,如果设y=x2﹣3x,那么原方程可化为关于y的整式方程是 .
12.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,从盒子中任意摸出1个球,若摸出红球的概率是0.2,那么n= .
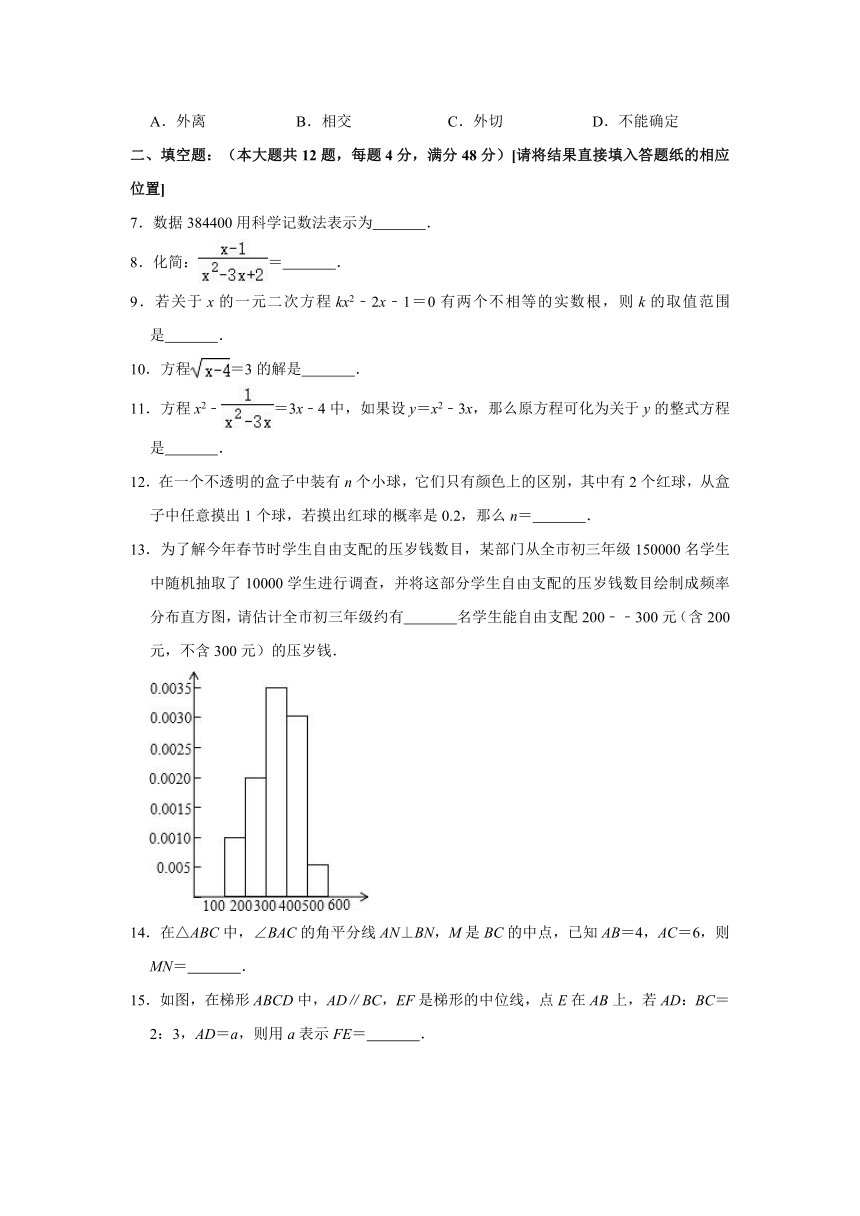
13.为了解今年春节时学生自由支配的压岁钱数目,某部门从全市初三年级150000名学生中随机抽取了10000学生进行调查,并将这部分学生自由支配的压岁钱数目绘制成频率分布直方图,请估计全市初三年级约有 名学生能自由支配200﹣﹣300元(含200元,不含300元)的压岁钱.
14.在△ABC中,∠BAC的角平分线AN⊥BN,M是BC的中点,已知AB=4,AC=6,则MN= .
15.如图,在梯形ABCD中,AD∥BC,EF是梯形的中位线,点E在AB上,若AD:BC=2:3,AD=a,则用a表示FE= .
16.若正四边形的半径是1,则它的边长是 .
17.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”是(1,2)的点的个数共有 个.
18.如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为 .
三、解答题(本大题共7题,满分78分)
19.计算:(+1)0﹣|sin60°﹣1|﹣+(﹣1)3
20.解不等式组:,并把数集在数轴上表示出来.
21.在△ABC中,∠ABC的角平分线交AC边于点D.
(1)用尺规作∠ABC的角平分线BD(不写作法,保留作图痕迹)
(2)若BD=9,sin∠DBC=,BC=,求tanC.
22.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
(1)分别求出甲、乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系及定义域;
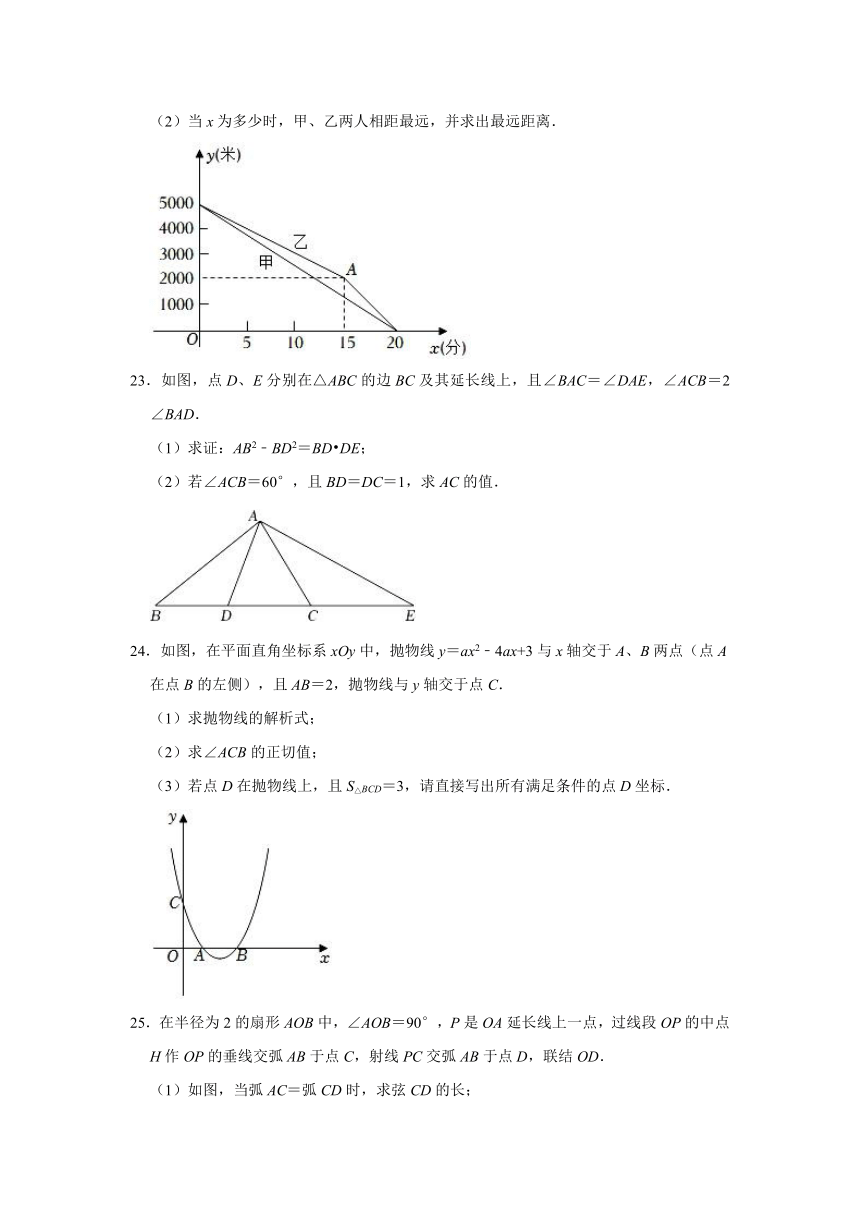
(2)当x为多少时,甲、乙两人相距最远,并求出最远距离.
23.如图,点D、E分别在△ABC的边BC及其延长线上,且∠BAC=∠DAE,∠ACB=2∠BAD.
(1)求证:AB2﹣BD2=BD DE;
(2)若∠ACB=60°,且BD=DC=1,求AC的值.
24.如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+3与x轴交于A、B两点(点A在点B的左侧),且AB=2,抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求∠ACB的正切值;
(3)若点D在抛物线上,且S△BCD=3,请直接写出所有满足条件的点D坐标.
25.在半径为2的扇形AOB中,∠AOB=90°,P是OA延长线上一点,过线段OP的中点H作OP的垂线交弧AB于点C,射线PC交弧AB于点D,联结OD.
(1)如图,当弧AC=弧CD时,求弦CD的长;
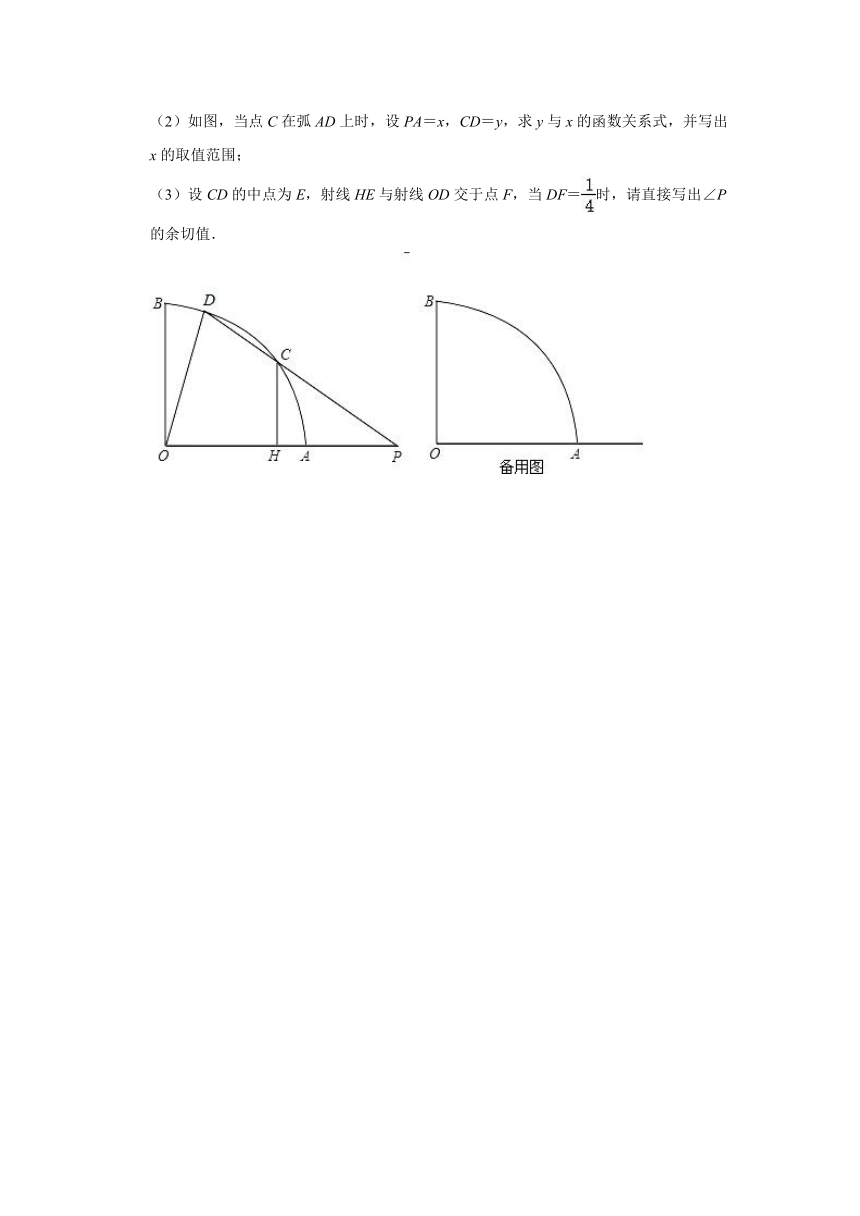
(2)如图,当点C在弧AD上时,设PA=x,CD=y,求y与x的函数关系式,并写出x的取值范围;
(3)设CD的中点为E,射线HE与射线OD交于点F,当DF=时,请直接写出∠P的余切值.
参考答案
一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.下列属于单项式的是( )
A.a+b B. C. D.1
【分析】数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式,根据单项式的定义即可判断.
解:A、是多项式,故本选项不符合题意;
B、是分式,不是单项式,故本选项不符合题意;
C、是多项式,故本选项不符合题意;
D、是单项式,故本选项符合题意;
故选:D.
2.下列运算中,正确的是( )
A.2x4﹣3x2=﹣x2 B.2x4+3x2=5x6
C.2x4 3x2=6x8 D.2x4 3x2=6x6
【分析】根据同类项,合并同类项法则,单项式乘以单项式法则,同底数幂的乘法求出每个式子的值,再判断即可.
解:A、2x4和﹣3x2不能合并,故本选项错误;
B、2x4和3x2不能合并,故本选项错误;
C、2x4 3x2=6x6,故本选项错误;
D、2x4 3x2=6x6,故本选项正确;
故选:D.
3.已知A(1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m>﹣ D.m<﹣
【分析】根据已知得3+2m>0,从而得出m的取值范围.
解:∵点A(1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,
∴3+2m>0,
∴m>﹣,
∴m的取值范围是m>﹣,
故选:C.
4.某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )
年龄(单位:岁) 14 15 16 17 18
人数 3 3 5 3 2
A.16,17 B.16,16 C.16,16.5 D.3,17
【分析】根据中位数、众数的意义进行计算即可.
解:篮球队16名队员的年龄出现次数最多的是16岁,共出现5次,因此众数是16岁,
将这16名队员的年龄从小到大排列,处在中间位置的两个数都是16岁,因此中位数是16岁,
故选:B.
5.下列命题中,假命题是( )
A.对角线垂直的平行四边形是菱形
B.对角线互相平分且垂直的四边形是菱形
C.对角线互相平分且平分一组内角的四边形是菱形
D.对角线相等且垂直的四边形是菱形
【分析】利用菱形的判定定理分别对每个选项逐一判断后即可得到正确的选项.
解:A、正确,是真命题;
B、正确,是真命题;
C、正确,是真命题;
D、对角线相等且垂直的四边形也可能是等腰梯形,故错误,是假命题,
故选:D.
6.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,DE∥BC,且AD=2CD,则以点C为圆心、DC长为半径的圆C和以点E为圆心、EB长为半径的圆E的位置关系是( )
A.外离 B.相交 C.外切 D.不能确定
【分析】根据勾股定理得到AC==4,根据相似三角形的性质得到BE=,CD=,DE=2,求得CE===,于是得到结论.
解:∵∠C=90°,AB=5,BC=3,
∴AC==4,
∵DE∥BC,
∴△ADE∽△ACB,
∴==,
∵AD=2CD,
∴=,
∴BE=,CD=,DE=2,
∴CE===,
∵BE+CD=>,
∴以点C为圆心、DC长为半径的圆C和以点E为圆心、EB长为半径的圆E的位置关系是相交,
故选:B.
二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置]
7.数据384400用科学记数法表示为 3.844×105 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于384400有6位,所以可以确定n=6﹣1=5.
解:384 400=3.844×105.
故答案为:3.844×105.
8.化简:= .
【分析】先利用“十字相乘法”对分母进行因式分解,然后通过约分进行化简.
解:
=
=.
故答案是:.
9.若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是 k>﹣1且k≠0 .
【分析】由关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,即可得判别式Δ>0且k≠0,则可求得k的取值范围.
解:∵关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,
∴Δ=b2﹣4ac=(﹣2)2﹣4×k×(﹣1)=4+4k>0,
∴k>﹣1,
∵x的一元二次方程kx2﹣2x﹣1=0
∴k≠0,
∴k的取值范围是:k>﹣1且k≠0.
故答案为:k>﹣1且k≠0.
10.方程=3的解是 x=13 .
【分析】因为x﹣4的算术平方根为3,所以得x﹣4=9,再解即可.
解:=3,
x﹣4=9,
x=13.
故答案为:x=13.
11.方程x2﹣=3x﹣4中,如果设y=x2﹣3x,那么原方程可化为关于y的整式方程是 y2+4y﹣1=0 .
【分析】移项观察,方程各项具备倒数关系,设y=x2﹣3x,则原方程另一个分式为.可用换元法转化为关于y的分式方程.去分母即可.
解:原方程移项得:x2﹣3x﹣+4=0中,
把y=x2﹣3x代入原方程得:y﹣+4=0,
方程两边同乘以y整理得:y2+4y﹣1=0.
故答案为:y2+4y﹣1=0.
12.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,从盒子中任意摸出1个球,若摸出红球的概率是0.2,那么n= 10 .
【分析】根据概率的求法,找准两点:
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
使用树状图分析时,一定要做到不重不漏.
解:根据题意得:=0.2,
解得:n=10.
13.为了解今年春节时学生自由支配的压岁钱数目,某部门从全市初三年级150000名学生中随机抽取了10000学生进行调查,并将这部分学生自由支配的压岁钱数目绘制成频率分布直方图,请估计全市初三年级约有 30000 名学生能自由支配200﹣﹣300元(含200元,不含300元)的压岁钱.
【分析】根据图上所给出的数据可知每组的组距为100,求出第二组的频率,再用全市初三年级的总人数乘以频率,即可得出答案.
解:根据题意得:150000×(100×0.0020)=30000(名),
答:全市初三年级约有30000名学生能自由支配200﹣﹣300元(含200元,不含300元)的压岁钱.
故答案为:30000.
14.在△ABC中,∠BAC的角平分线AN⊥BN,M是BC的中点,已知AB=4,AC=6,则MN= 1 .
【分析】延长线段BN,交AC于E,利用已知易证△ABN≌△AEN,所以BN=EN,从而证得MN是△BCE的中位线,所以求出EC,再运用中位线定理求MN.
解:延长线段BN,交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN.
∵在△ABN与△AEN中,
,
∴△ABN≌△AEN(ASA).
∴AE=AB=14,BN=NE.
又∵M是△ABC的边BC的中点,
故MN=EC=(AC﹣AE)=(6﹣4)=1.
故答案是:1.
15.如图,在梯形ABCD中,AD∥BC,EF是梯形的中位线,点E在AB上,若AD:BC=2:3,AD=a,则用a表示FE= a .
【分析】利用梯形的中位线定理求解即可.
解:∵AD:BC=2:3,AD=a,
∴BC=a,
∵EF是梯形ABCD的中位线,
∴EF=(AD+BC)=(a+a)=a,
故答案为:a.
16.若正四边形的半径是1,则它的边长是 .
【分析】首先根据题意画出图形,由四边形ABCD是正四边形,可得∠AOB=90°,然后由勾股定理求得它的边长.
解:如图:根据题意得:OA=OB=1,
∵四边形ABCD是正四边形,
∴∠AOB=90°,
∴AB==.
即它的边长是:.
故答案为:.
17.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”是(1,2)的点的个数共有 4 个.
【分析】根据“距离坐标”分别写出各点即可得解.
解:“距离坐标”是(1,2)的点有M1,M2,M3,M4共4个.
如图:
故答案为:4.
18.如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为 48 .
【分析】根据点G是△ABC的重心,CG的延长线交AB于D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,得出DG=DE=4,以及BE=10,即可得出△EBG的面积,进而得出答案.
解:∵点G是△ABC的重心,CG的延长线交AB于D,GC=8,
∴DE=4,
∵将△ADG绕点D顺时针方向旋转180°得到△BDE,
∴DG=DE=4,AG=BE=10,∵BG=6,
∵62+82=102,
∴△BGE是直角三角形,
∴△BGE的面积为:×6×8=24,
∵∠BGE=90°,
∴∠BGC=90°,
∴△BGC的面积为:×6×8=24,
∴△EBC的面积为:48.
故答案为:48.
三、解答题(本大题共7题,满分78分)
19.计算:(+1)0﹣|sin60°﹣1|﹣+(﹣1)3
【分析】由于(+1)0=1;|sin60°﹣1|=1﹣;=;(﹣1)3=﹣1.由此即可求解.
解:原式=1﹣(1﹣)﹣﹣1
=﹣﹣1
=﹣.
20.解不等式组:,并把数集在数轴上表示出来.
【分析】先求出每个不等式的解集,找出不等式组的解集,最后在数轴上表示出来即可.
解:∵由①得:x>﹣1,
由②得:x≤3,
∴原不等式组的解集为:﹣1<x≤3,
在数轴上表示为.
21.在△ABC中,∠ABC的角平分线交AC边于点D.
(1)用尺规作∠ABC的角平分线BD(不写作法,保留作图痕迹)
(2)若BD=9,sin∠DBC=,BC=,求tanC.
【分析】(1)①以点B为圆心,以任意长为半径画弧,两弧交角ABC两边于点M,N;
②分别以点M,N为圆心,以大于MN的长度为半径画弧,两弧交于点E;
③作射线BE交AC与D.
则线段BD为△ABC的角平分线.
(2)过点D作DE⊥BC,垂足为点E,首先求得DE,然后利用勾股定理求得BE,从而根据BC的长求得EC,然后利用正切的定义求得答案即可.
解:(1)如图:
(2)过点D作DE⊥BC,垂足为点E,
∵在Rt△BDE中,BD=9,sin∠DBC=,
∴DE=3,
∴BE==6,
∵BC=,
∴EC=,
∴在Rt△DEC中,
∴tanC===.
22.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
(1)分别求出甲、乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系及定义域;
(2)当x为多少时,甲、乙两人相距最远,并求出最远距离.
【分析】(1)观察函数图象,根据图中给出的点的坐标,利用待定系数法即可求出甲、乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式及定义域;
(2)
解:(1)设甲在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式为y=k1x+b1(k1≠0),
将(0,5000),(20,0)代入y=k1x+b1得:,
解得:,
∴甲在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式为y=﹣250x+5000(0≤x≤20).
当0≤x≤15时,设乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=k2x+b2(k2≠0),
将(0,5000),(15,2000)代入y=k2x+b2得:,
解得:,
∴乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=﹣200x+5000(0≤x≤15);
当15<x≤20时,设乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=k3x+b3(k3≠0),
将(15,2000),(20,0)代入y=k3x+b3得:,
解得:,
∴乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=﹣400x+8000(15<x≤20).
∴乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式为.
(2)由图可知,当x=15时,甲、乙两人相距最远,
当x=15时,y=﹣250×15+5000=1250,
2000﹣1250=750(米),
即最大距离为750米.
∴当x=15时,甲、乙两人相距最远,最远距离为750米.
23.如图,点D、E分别在△ABC的边BC及其延长线上,且∠BAC=∠DAE,∠ACB=2∠BAD.
(1)求证:AB2﹣BD2=BD DE;
(2)若∠ACB=60°,且BD=DC=1,求AC的值.
【分析】(1)通过证明△BAD∽△BEA,可得,可得结论;
(2)由直角三角形的性质可求,,由勾股定理可求解.
【解答】(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
设∠BAD=∠CAE=α,
由∠ACB=2∠BAD=2α,
∴∠E=∠ACB﹣∠CAE=2α﹣α=α,
∴∠BAD=∠E=α,
又∠B=∠B,
∴△BAD∽△BEA,
∴,
即AB2=BD BE=BD (BD+DE)=BD2+BD DE,
∴AB2﹣BD2=BD DE.
(2)解:作AF⊥BC于点F,
设AC=x,
∵∠CAE=∠E=α,
∴CE=AC=x,
又∵∠ACB=60°,
∴,,
又∵BD=DC=1,
∴,
由勾股定理得,AB2=BF2+AF2,
又∵AB2=BD BE,
∴BF2+AF2=BD BE,
∴(2﹣x)2+(x)2=1×(2+x),
∴x1=1,x2=2,
∴AC的值为1或2.
24.如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+3与x轴交于A、B两点(点A在点B的左侧),且AB=2,抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求∠ACB的正切值;
(3)若点D在抛物线上,且S△BCD=3,请直接写出所有满足条件的点D坐标.
【分析】(1)由抛物线的解析式求得对称轴为直线x=2,然后由AB=2求得点A的坐标为(1,0),点B的坐标为(3,0),从而代入点A得到抛物线的解析式;
(2)过点A作AH⊥BC于点H,先求得点C的坐标,然后得到OC,OB,BC的长,求得△OBC是等腰直角三角形,从而得到△ABH是等腰直角三角形,再由AB=2求得AH、BH的长,再求得CH的长,最后即可求得∠ACB的正切值;
(3)先求得△ABC的面积为3,由△BCD的面积为3得知两三角形的面积相等,结合两三角形具有公共边,从而得到△BCD边BC上的高与AH长度相等,①当点D在直线BC下方时,过点A作直线BC的平行线,交y轴于点E,交抛物线于点D1,D2,先求得直线BC的解析式,再由直线平行的性质求得直线AE的解析式,再联立直线AE和抛物线的解析式求得点D1,D2;②当点D在直线BC上方时,取点FC=EC,过点F作BC的平行线,交抛物线于点D3,D4,由点F的坐标求得直线D3D4的解析式,再联立直线D3D4和抛物线的解析式求得点D3,D4的坐标.
解:(1)∵y=ax2﹣4ax+3,
∴抛物线的对称轴为直线x=﹣=2,
又∵AB=2,
∴点A的坐标为(1,0),点B的坐标为(3,0),
将点A(1,0)代入y=ax2﹣4ax+3得:a﹣4a+3=0,
解得:a=1,
∴抛物线的解析式为y=x2﹣4x+3.
(2)过点A作AH⊥BC于点H,则∠AHC=∠AHB=90°,
对y=x2﹣4x+3,当x=0时,y=3,
∴C(0,3),
又∵O(0,0),A(1,0),B(3,0),
∴BO=CO=3,BC=3,
∵∠COB=90°,
∴△OBC是等腰直角三角形,
∴∠OBC=45°,
∴△ABH是等腰直角三角形,
∵AB=2,
∴AH=BH=,
∴CH=BC﹣BH=2,
∴tan∠ACB===;
(3)∵AB=2,OC=3,
∴S△ABC=×2×3=3,
∴S△ABC=S△BCD=3,
∴△BCD边BC上的高与AH长度相等,
①当点D在直线BC下方时,过点A作直线BC的平行线,交y轴于点E,交抛物线于点D1,D2,
设直线BC的解析式为y=kx+b,则
,解得:,
∴直线BC的解析式为y=﹣x+3,
设直线AE的解析式为y=﹣x+b,
将点A(1,0)代入y=﹣x+b,得﹣1+b=0,
∴b=1,
∴E(0,1),直线AE的解析式为y=﹣x+1,
由,解得:或,
∴点D1(2,﹣1),D2(1,0);
②当点D在直线BC上方时,取点FC=EC,过点F作BC的平行线,交抛物线于点D3,D4,则F(0,5),
设直线D3D4的解析式为y=﹣x+m,
将点F代入y=﹣x+m,得m=5,
∴直线D3D4的解析式为y=﹣x+5,
由,解得:或,
∴,,
综上所述,当S△BCD=3时,满足条件的点D坐标的坐标为D1(2,﹣1),D2(1,0),,.
25.在半径为2的扇形AOB中,∠AOB=90°,P是OA延长线上一点,过线段OP的中点H作OP的垂线交弧AB于点C,射线PC交弧AB于点D,联结OD.
(1)如图,当弧AC=弧CD时,求弦CD的长;
(2)如图,当点C在弧AD上时,设PA=x,CD=y,求y与x的函数关系式,并写出x的取值范围;
(3)设CD的中点为E,射线HE与射线OD交于点F,当DF=时,请直接写出∠P的余切值.
【分析】(1)根据弧AC=弧CD,得出∠DOC=∠AOC,进而求出PC=OC,以及△DOC∽△DPO,再利用相似三角形的性质得出即可;
(2)根据切割线定理即可求得.
(3)利用等腰三角形的性质以及锐角三角函数关系即可得出tan∠P的值.
【解答】
解:如图1,(1)联结CO,∵HC垂直平分OP,
∴CP=CO=2,
∴∠COP=∠P,
∵=,
∴∠COP=∠DOC,
∴∠DOC=∠P,
又∵∠ODC=∠PDO,
∴△DOC∽△DPO,
∴=
又CP=OD=OC=2,
∴=,
∴4=DC(DC+2),
解得:CD=﹣1+,CD=﹣1﹣(舍去)
(2)根据割线定理可知:PC PD=PA (AP+OA)
∵PC=OC=2,
∴2(2+y)=x(x+4),
∴y=x2+2x﹣2,(2﹣2≤x≤2﹣2)
(3)如图2,连接OC和OE.
显然可以得:Rt△CHP≌Rt△CHO,
∴∠CPH=∠COH=x(不妨设其大小为x)
∴∠DCO=2x.(三角形外角的性质定理),
同时,PC=OC=2,
∵CE=DE(已知)
∴由垂径定理可知:OE⊥CD,
∵OD=OC,
∴∠ODC=∠OCD=2x.
同时,由锐角三角函数定义,
在Rt△OPE中.
tan∠APD=,
∵∠CHO=∠CEO=90°,
∴四点H,C,E,O四点共圆,
∴由同圆中,同弧上的圆周角相等可知
∠HEC=∠HOC=x,
∴∠DEF=∠HEC=∠HOC=x.
在△DEF中,由三角形外角性质定理,
∠ODC=∠F+∠DEF,
∴2x=∠F+x,
∴∠F=x.
∴△DEF为等腰三角形,
CE=DE=DF=.
∴PE=PC+CE=2+=,
在Rt△ODE中,DE=,OD=2,
∴由勾股定理可得OE=,
∴cot∠P===,
一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.下列属于单项式的是( )
A.a+b B. C. D.1
2.下列运算中,正确的是( )
A.2x4﹣3x2=﹣x2 B.2x4+3x2=5x6
C.2x4 3x2=6x8 D.2x4 3x2=6x6
3.已知A(1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m>﹣ D.m<﹣
4.某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )
年龄(单位:岁) 14 15 16 17 18
人数 3 3 5 3 2
A.16,17 B.16,16 C.16,16.5 D.3,17
5.下列命题中,假命题是( )
A.对角线垂直的平行四边形是菱形
B.对角线互相平分且垂直的四边形是菱形
C.对角线互相平分且平分一组内角的四边形是菱形
D.对角线相等且垂直的四边形是菱形
6.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,DE∥BC,且AD=2CD,则以点C为圆心、DC长为半径的圆C和以点E为圆心、EB长为半径的圆E的位置关系是( )
A.外离 B.相交 C.外切 D.不能确定
二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置]
7.数据384400用科学记数法表示为 .
8.化简:= .
9.若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是 .
10.方程=3的解是 .
11.方程x2﹣=3x﹣4中,如果设y=x2﹣3x,那么原方程可化为关于y的整式方程是 .
12.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,从盒子中任意摸出1个球,若摸出红球的概率是0.2,那么n= .
13.为了解今年春节时学生自由支配的压岁钱数目,某部门从全市初三年级150000名学生中随机抽取了10000学生进行调查,并将这部分学生自由支配的压岁钱数目绘制成频率分布直方图,请估计全市初三年级约有 名学生能自由支配200﹣﹣300元(含200元,不含300元)的压岁钱.
14.在△ABC中,∠BAC的角平分线AN⊥BN,M是BC的中点,已知AB=4,AC=6,则MN= .
15.如图,在梯形ABCD中,AD∥BC,EF是梯形的中位线,点E在AB上,若AD:BC=2:3,AD=a,则用a表示FE= .
16.若正四边形的半径是1,则它的边长是 .
17.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”是(1,2)的点的个数共有 个.
18.如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为 .
三、解答题(本大题共7题,满分78分)
19.计算:(+1)0﹣|sin60°﹣1|﹣+(﹣1)3
20.解不等式组:,并把数集在数轴上表示出来.
21.在△ABC中,∠ABC的角平分线交AC边于点D.
(1)用尺规作∠ABC的角平分线BD(不写作法,保留作图痕迹)
(2)若BD=9,sin∠DBC=,BC=,求tanC.
22.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
(1)分别求出甲、乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系及定义域;
(2)当x为多少时,甲、乙两人相距最远,并求出最远距离.
23.如图,点D、E分别在△ABC的边BC及其延长线上,且∠BAC=∠DAE,∠ACB=2∠BAD.
(1)求证:AB2﹣BD2=BD DE;
(2)若∠ACB=60°,且BD=DC=1,求AC的值.
24.如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+3与x轴交于A、B两点(点A在点B的左侧),且AB=2,抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求∠ACB的正切值;
(3)若点D在抛物线上,且S△BCD=3,请直接写出所有满足条件的点D坐标.
25.在半径为2的扇形AOB中,∠AOB=90°,P是OA延长线上一点,过线段OP的中点H作OP的垂线交弧AB于点C,射线PC交弧AB于点D,联结OD.
(1)如图,当弧AC=弧CD时,求弦CD的长;
(2)如图,当点C在弧AD上时,设PA=x,CD=y,求y与x的函数关系式,并写出x的取值范围;
(3)设CD的中点为E,射线HE与射线OD交于点F,当DF=时,请直接写出∠P的余切值.
参考答案
一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.下列属于单项式的是( )
A.a+b B. C. D.1
【分析】数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式,根据单项式的定义即可判断.
解:A、是多项式,故本选项不符合题意;
B、是分式,不是单项式,故本选项不符合题意;
C、是多项式,故本选项不符合题意;
D、是单项式,故本选项符合题意;
故选:D.
2.下列运算中,正确的是( )
A.2x4﹣3x2=﹣x2 B.2x4+3x2=5x6
C.2x4 3x2=6x8 D.2x4 3x2=6x6
【分析】根据同类项,合并同类项法则,单项式乘以单项式法则,同底数幂的乘法求出每个式子的值,再判断即可.
解:A、2x4和﹣3x2不能合并,故本选项错误;
B、2x4和3x2不能合并,故本选项错误;
C、2x4 3x2=6x6,故本选项错误;
D、2x4 3x2=6x6,故本选项正确;
故选:D.
3.已知A(1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m>﹣ D.m<﹣
【分析】根据已知得3+2m>0,从而得出m的取值范围.
解:∵点A(1,y1),B(2,y2)两点在双曲线y=上,且y1>y2,
∴3+2m>0,
∴m>﹣,
∴m的取值范围是m>﹣,
故选:C.
4.某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )
年龄(单位:岁) 14 15 16 17 18
人数 3 3 5 3 2
A.16,17 B.16,16 C.16,16.5 D.3,17
【分析】根据中位数、众数的意义进行计算即可.
解:篮球队16名队员的年龄出现次数最多的是16岁,共出现5次,因此众数是16岁,
将这16名队员的年龄从小到大排列,处在中间位置的两个数都是16岁,因此中位数是16岁,
故选:B.
5.下列命题中,假命题是( )
A.对角线垂直的平行四边形是菱形
B.对角线互相平分且垂直的四边形是菱形
C.对角线互相平分且平分一组内角的四边形是菱形
D.对角线相等且垂直的四边形是菱形
【分析】利用菱形的判定定理分别对每个选项逐一判断后即可得到正确的选项.
解:A、正确,是真命题;
B、正确,是真命题;
C、正确,是真命题;
D、对角线相等且垂直的四边形也可能是等腰梯形,故错误,是假命题,
故选:D.
6.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,DE∥BC,且AD=2CD,则以点C为圆心、DC长为半径的圆C和以点E为圆心、EB长为半径的圆E的位置关系是( )
A.外离 B.相交 C.外切 D.不能确定
【分析】根据勾股定理得到AC==4,根据相似三角形的性质得到BE=,CD=,DE=2,求得CE===,于是得到结论.
解:∵∠C=90°,AB=5,BC=3,
∴AC==4,
∵DE∥BC,
∴△ADE∽△ACB,
∴==,
∵AD=2CD,
∴=,
∴BE=,CD=,DE=2,
∴CE===,
∵BE+CD=>,
∴以点C为圆心、DC长为半径的圆C和以点E为圆心、EB长为半径的圆E的位置关系是相交,
故选:B.
二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置]
7.数据384400用科学记数法表示为 3.844×105 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于384400有6位,所以可以确定n=6﹣1=5.
解:384 400=3.844×105.
故答案为:3.844×105.
8.化简:= .
【分析】先利用“十字相乘法”对分母进行因式分解,然后通过约分进行化简.
解:
=
=.
故答案是:.
9.若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是 k>﹣1且k≠0 .
【分析】由关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,即可得判别式Δ>0且k≠0,则可求得k的取值范围.
解:∵关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,
∴Δ=b2﹣4ac=(﹣2)2﹣4×k×(﹣1)=4+4k>0,
∴k>﹣1,
∵x的一元二次方程kx2﹣2x﹣1=0
∴k≠0,
∴k的取值范围是:k>﹣1且k≠0.
故答案为:k>﹣1且k≠0.
10.方程=3的解是 x=13 .
【分析】因为x﹣4的算术平方根为3,所以得x﹣4=9,再解即可.
解:=3,
x﹣4=9,
x=13.
故答案为:x=13.
11.方程x2﹣=3x﹣4中,如果设y=x2﹣3x,那么原方程可化为关于y的整式方程是 y2+4y﹣1=0 .
【分析】移项观察,方程各项具备倒数关系,设y=x2﹣3x,则原方程另一个分式为.可用换元法转化为关于y的分式方程.去分母即可.
解:原方程移项得:x2﹣3x﹣+4=0中,
把y=x2﹣3x代入原方程得:y﹣+4=0,
方程两边同乘以y整理得:y2+4y﹣1=0.
故答案为:y2+4y﹣1=0.
12.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,从盒子中任意摸出1个球,若摸出红球的概率是0.2,那么n= 10 .
【分析】根据概率的求法,找准两点:
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
使用树状图分析时,一定要做到不重不漏.
解:根据题意得:=0.2,
解得:n=10.
13.为了解今年春节时学生自由支配的压岁钱数目,某部门从全市初三年级150000名学生中随机抽取了10000学生进行调查,并将这部分学生自由支配的压岁钱数目绘制成频率分布直方图,请估计全市初三年级约有 30000 名学生能自由支配200﹣﹣300元(含200元,不含300元)的压岁钱.
【分析】根据图上所给出的数据可知每组的组距为100,求出第二组的频率,再用全市初三年级的总人数乘以频率,即可得出答案.
解:根据题意得:150000×(100×0.0020)=30000(名),
答:全市初三年级约有30000名学生能自由支配200﹣﹣300元(含200元,不含300元)的压岁钱.
故答案为:30000.
14.在△ABC中,∠BAC的角平分线AN⊥BN,M是BC的中点,已知AB=4,AC=6,则MN= 1 .
【分析】延长线段BN,交AC于E,利用已知易证△ABN≌△AEN,所以BN=EN,从而证得MN是△BCE的中位线,所以求出EC,再运用中位线定理求MN.
解:延长线段BN,交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN.
∵在△ABN与△AEN中,
,
∴△ABN≌△AEN(ASA).
∴AE=AB=14,BN=NE.
又∵M是△ABC的边BC的中点,
故MN=EC=(AC﹣AE)=(6﹣4)=1.
故答案是:1.
15.如图,在梯形ABCD中,AD∥BC,EF是梯形的中位线,点E在AB上,若AD:BC=2:3,AD=a,则用a表示FE= a .
【分析】利用梯形的中位线定理求解即可.
解:∵AD:BC=2:3,AD=a,
∴BC=a,
∵EF是梯形ABCD的中位线,
∴EF=(AD+BC)=(a+a)=a,
故答案为:a.
16.若正四边形的半径是1,则它的边长是 .
【分析】首先根据题意画出图形,由四边形ABCD是正四边形,可得∠AOB=90°,然后由勾股定理求得它的边长.
解:如图:根据题意得:OA=OB=1,
∵四边形ABCD是正四边形,
∴∠AOB=90°,
∴AB==.
即它的边长是:.
故答案为:.
17.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”是(1,2)的点的个数共有 4 个.
【分析】根据“距离坐标”分别写出各点即可得解.
解:“距离坐标”是(1,2)的点有M1,M2,M3,M4共4个.
如图:
故答案为:4.
18.如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为 48 .
【分析】根据点G是△ABC的重心,CG的延长线交AB于D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,得出DG=DE=4,以及BE=10,即可得出△EBG的面积,进而得出答案.
解:∵点G是△ABC的重心,CG的延长线交AB于D,GC=8,
∴DE=4,
∵将△ADG绕点D顺时针方向旋转180°得到△BDE,
∴DG=DE=4,AG=BE=10,∵BG=6,
∵62+82=102,
∴△BGE是直角三角形,
∴△BGE的面积为:×6×8=24,
∵∠BGE=90°,
∴∠BGC=90°,
∴△BGC的面积为:×6×8=24,
∴△EBC的面积为:48.
故答案为:48.
三、解答题(本大题共7题,满分78分)
19.计算:(+1)0﹣|sin60°﹣1|﹣+(﹣1)3
【分析】由于(+1)0=1;|sin60°﹣1|=1﹣;=;(﹣1)3=﹣1.由此即可求解.
解:原式=1﹣(1﹣)﹣﹣1
=﹣﹣1
=﹣.
20.解不等式组:,并把数集在数轴上表示出来.
【分析】先求出每个不等式的解集,找出不等式组的解集,最后在数轴上表示出来即可.
解:∵由①得:x>﹣1,
由②得:x≤3,
∴原不等式组的解集为:﹣1<x≤3,
在数轴上表示为.
21.在△ABC中,∠ABC的角平分线交AC边于点D.
(1)用尺规作∠ABC的角平分线BD(不写作法,保留作图痕迹)
(2)若BD=9,sin∠DBC=,BC=,求tanC.
【分析】(1)①以点B为圆心,以任意长为半径画弧,两弧交角ABC两边于点M,N;
②分别以点M,N为圆心,以大于MN的长度为半径画弧,两弧交于点E;
③作射线BE交AC与D.
则线段BD为△ABC的角平分线.
(2)过点D作DE⊥BC,垂足为点E,首先求得DE,然后利用勾股定理求得BE,从而根据BC的长求得EC,然后利用正切的定义求得答案即可.
解:(1)如图:
(2)过点D作DE⊥BC,垂足为点E,
∵在Rt△BDE中,BD=9,sin∠DBC=,
∴DE=3,
∴BE==6,
∵BC=,
∴EC=,
∴在Rt△DEC中,
∴tanC===.
22.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
(1)分别求出甲、乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系及定义域;
(2)当x为多少时,甲、乙两人相距最远,并求出最远距离.
【分析】(1)观察函数图象,根据图中给出的点的坐标,利用待定系数法即可求出甲、乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式及定义域;
(2)
解:(1)设甲在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式为y=k1x+b1(k1≠0),
将(0,5000),(20,0)代入y=k1x+b1得:,
解得:,
∴甲在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式为y=﹣250x+5000(0≤x≤20).
当0≤x≤15时,设乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=k2x+b2(k2≠0),
将(0,5000),(15,2000)代入y=k2x+b2得:,
解得:,
∴乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=﹣200x+5000(0≤x≤15);
当15<x≤20时,设乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=k3x+b3(k3≠0),
将(15,2000),(20,0)代入y=k3x+b3得:,
解得:,
∴乙距离终点的路程y(米)和跑步时间x(分)之间的函数关系为y=﹣400x+8000(15<x≤20).
∴乙在整个过程中距离终点的路程y(米)和跑步时间x(分)之间的函数关系式为.
(2)由图可知,当x=15时,甲、乙两人相距最远,
当x=15时,y=﹣250×15+5000=1250,
2000﹣1250=750(米),
即最大距离为750米.
∴当x=15时,甲、乙两人相距最远,最远距离为750米.
23.如图,点D、E分别在△ABC的边BC及其延长线上,且∠BAC=∠DAE,∠ACB=2∠BAD.
(1)求证:AB2﹣BD2=BD DE;
(2)若∠ACB=60°,且BD=DC=1,求AC的值.
【分析】(1)通过证明△BAD∽△BEA,可得,可得结论;
(2)由直角三角形的性质可求,,由勾股定理可求解.
【解答】(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
设∠BAD=∠CAE=α,
由∠ACB=2∠BAD=2α,
∴∠E=∠ACB﹣∠CAE=2α﹣α=α,
∴∠BAD=∠E=α,
又∠B=∠B,
∴△BAD∽△BEA,
∴,
即AB2=BD BE=BD (BD+DE)=BD2+BD DE,
∴AB2﹣BD2=BD DE.
(2)解:作AF⊥BC于点F,
设AC=x,
∵∠CAE=∠E=α,
∴CE=AC=x,
又∵∠ACB=60°,
∴,,
又∵BD=DC=1,
∴,
由勾股定理得,AB2=BF2+AF2,
又∵AB2=BD BE,
∴BF2+AF2=BD BE,
∴(2﹣x)2+(x)2=1×(2+x),
∴x1=1,x2=2,
∴AC的值为1或2.
24.如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+3与x轴交于A、B两点(点A在点B的左侧),且AB=2,抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求∠ACB的正切值;
(3)若点D在抛物线上,且S△BCD=3,请直接写出所有满足条件的点D坐标.
【分析】(1)由抛物线的解析式求得对称轴为直线x=2,然后由AB=2求得点A的坐标为(1,0),点B的坐标为(3,0),从而代入点A得到抛物线的解析式;
(2)过点A作AH⊥BC于点H,先求得点C的坐标,然后得到OC,OB,BC的长,求得△OBC是等腰直角三角形,从而得到△ABH是等腰直角三角形,再由AB=2求得AH、BH的长,再求得CH的长,最后即可求得∠ACB的正切值;
(3)先求得△ABC的面积为3,由△BCD的面积为3得知两三角形的面积相等,结合两三角形具有公共边,从而得到△BCD边BC上的高与AH长度相等,①当点D在直线BC下方时,过点A作直线BC的平行线,交y轴于点E,交抛物线于点D1,D2,先求得直线BC的解析式,再由直线平行的性质求得直线AE的解析式,再联立直线AE和抛物线的解析式求得点D1,D2;②当点D在直线BC上方时,取点FC=EC,过点F作BC的平行线,交抛物线于点D3,D4,由点F的坐标求得直线D3D4的解析式,再联立直线D3D4和抛物线的解析式求得点D3,D4的坐标.
解:(1)∵y=ax2﹣4ax+3,
∴抛物线的对称轴为直线x=﹣=2,
又∵AB=2,
∴点A的坐标为(1,0),点B的坐标为(3,0),
将点A(1,0)代入y=ax2﹣4ax+3得:a﹣4a+3=0,
解得:a=1,
∴抛物线的解析式为y=x2﹣4x+3.
(2)过点A作AH⊥BC于点H,则∠AHC=∠AHB=90°,
对y=x2﹣4x+3,当x=0时,y=3,
∴C(0,3),
又∵O(0,0),A(1,0),B(3,0),
∴BO=CO=3,BC=3,
∵∠COB=90°,
∴△OBC是等腰直角三角形,
∴∠OBC=45°,
∴△ABH是等腰直角三角形,
∵AB=2,
∴AH=BH=,
∴CH=BC﹣BH=2,
∴tan∠ACB===;
(3)∵AB=2,OC=3,
∴S△ABC=×2×3=3,
∴S△ABC=S△BCD=3,
∴△BCD边BC上的高与AH长度相等,
①当点D在直线BC下方时,过点A作直线BC的平行线,交y轴于点E,交抛物线于点D1,D2,
设直线BC的解析式为y=kx+b,则
,解得:,
∴直线BC的解析式为y=﹣x+3,
设直线AE的解析式为y=﹣x+b,
将点A(1,0)代入y=﹣x+b,得﹣1+b=0,
∴b=1,
∴E(0,1),直线AE的解析式为y=﹣x+1,
由,解得:或,
∴点D1(2,﹣1),D2(1,0);
②当点D在直线BC上方时,取点FC=EC,过点F作BC的平行线,交抛物线于点D3,D4,则F(0,5),
设直线D3D4的解析式为y=﹣x+m,
将点F代入y=﹣x+m,得m=5,
∴直线D3D4的解析式为y=﹣x+5,
由,解得:或,
∴,,
综上所述,当S△BCD=3时,满足条件的点D坐标的坐标为D1(2,﹣1),D2(1,0),,.
25.在半径为2的扇形AOB中,∠AOB=90°,P是OA延长线上一点,过线段OP的中点H作OP的垂线交弧AB于点C,射线PC交弧AB于点D,联结OD.
(1)如图,当弧AC=弧CD时,求弦CD的长;
(2)如图,当点C在弧AD上时,设PA=x,CD=y,求y与x的函数关系式,并写出x的取值范围;
(3)设CD的中点为E,射线HE与射线OD交于点F,当DF=时,请直接写出∠P的余切值.
【分析】(1)根据弧AC=弧CD,得出∠DOC=∠AOC,进而求出PC=OC,以及△DOC∽△DPO,再利用相似三角形的性质得出即可;
(2)根据切割线定理即可求得.
(3)利用等腰三角形的性质以及锐角三角函数关系即可得出tan∠P的值.
【解答】
解:如图1,(1)联结CO,∵HC垂直平分OP,
∴CP=CO=2,
∴∠COP=∠P,
∵=,
∴∠COP=∠DOC,
∴∠DOC=∠P,
又∵∠ODC=∠PDO,
∴△DOC∽△DPO,
∴=
又CP=OD=OC=2,
∴=,
∴4=DC(DC+2),
解得:CD=﹣1+,CD=﹣1﹣(舍去)
(2)根据割线定理可知:PC PD=PA (AP+OA)
∵PC=OC=2,
∴2(2+y)=x(x+4),
∴y=x2+2x﹣2,(2﹣2≤x≤2﹣2)
(3)如图2,连接OC和OE.
显然可以得:Rt△CHP≌Rt△CHO,
∴∠CPH=∠COH=x(不妨设其大小为x)
∴∠DCO=2x.(三角形外角的性质定理),
同时,PC=OC=2,
∵CE=DE(已知)
∴由垂径定理可知:OE⊥CD,
∵OD=OC,
∴∠ODC=∠OCD=2x.
同时,由锐角三角函数定义,
在Rt△OPE中.
tan∠APD=,
∵∠CHO=∠CEO=90°,
∴四点H,C,E,O四点共圆,
∴由同圆中,同弧上的圆周角相等可知
∠HEC=∠HOC=x,
∴∠DEF=∠HEC=∠HOC=x.
在△DEF中,由三角形外角性质定理,
∠ODC=∠F+∠DEF,
∴2x=∠F+x,
∴∠F=x.
∴△DEF为等腰三角形,
CE=DE=DF=.
∴PE=PC+CE=2+=,
在Rt△ODE中,DE=,OD=2,
∴由勾股定理可得OE=,
∴cot∠P===,
同课章节目录
