5.4 圆周运动 课件(人教必修2)
文档属性
| 名称 | 5.4 圆周运动 课件(人教必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-12-27 21:19:25 | ||
图片预览











文档简介
课件42张PPT。第五章新知预习·巧设计名师课堂
·一点通要点一要点二第4节创新演练
·大冲关随堂检测归纳小结课下作业综合提升1. 理解匀速圆周运动的概念,知道匀
速圆周运动是变速运动。
2.理解匀速圆周运动的线速度和角速
度、周期、转速等描述圆周运动快
慢的概念。
3.掌握线速度、角速度、周期和频率
间的关系。[读教材·填要点]1.描述圆周运动的物理量
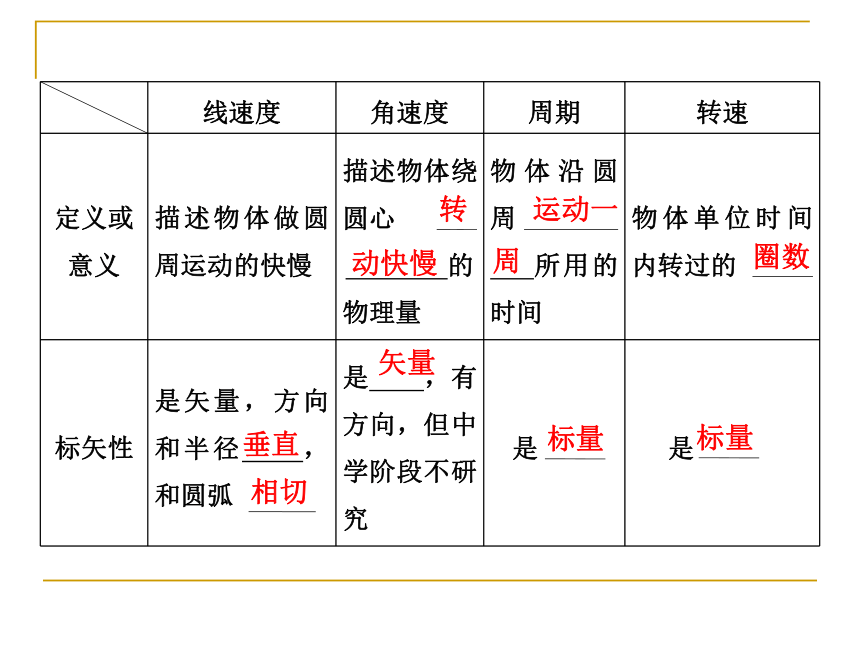
(1)圆周运动:物体沿着 的运动。
(2)描述圆周运动的物理量及相互关系圆周垂直相切转动快慢运动一周圈数标量标量矢量m/srad/ssr/s r/min [关键一点] 注意区别角速度的单位rad/s和转速的单位r/s,分别表示每秒转过的角度和圈数。2.匀速圆周运动
(1)定义:线速度的大小处处 的圆周运动。
(2)特点:
①线速度大小 ,方向 ,是一种 运动。
②角速度 。
③转速、 不变。相等不变时刻改变变速不变周期[试身手·夯基础]1.下列关于匀速圆周运动的说法中,正确的是 ( )
A.是线速度不变的运动
B.是角速度不变的运动
C.是角速度不断变化的运动
D.是相对圆心位移不变的运动
解析:匀速圆周运动,角速度保持不变,线速度大小保持不变,方向时刻变化,A、C错误,B正确;相对圆心的位移大小不变,方向时刻变化,D错误。
答案:B2.一质点做匀速圆周运动,其线速度大小为4 m/s,
转动周期为2 s,则不正确的是 ( )
A.角速度为0.5 rad/s
B.转速为0.5 r/s
C.运动轨迹的半径为1.27 m
D.频率为 Hz.答案:A3.质点做匀速圆周运动,则:
①在任何相等的时间里,质点的位移都相等
②在任何相等的时间里,质点通过的路程都相等
③在任何相等的时间里,质点运动的平均速度都相同
④在任何相等的时间里,连接质点和圆心的半径转过的角度都相等
以上说法中正确的是 ( )
A.①② B.③④
C.①③ D.②④解析:匀速圆周运动是变速运动,故在相等的时间内通过的路程相等,但位移不等,故①错,②正确。因为做匀速圆周运动的角速度不变,故④正确。平均速度是位移与时间的比值,所以③错。
答案:D4.光滑的水平面上固定着一个螺旋形光
滑轨道,俯视如图5-4-1所示。一个小球以一定速度沿轨道切线方向进入轨道,小球从进入轨道直到到达螺旋形中央区的时间内,关于小球运动的角速度和线速度大小变化的说法正确的是 ( )
A.增大、减小 B.不变、不变
C.增大、不变 D.减小、减小图5-4-1解析:由于轨道是光滑的,小球运动的线速度大小不变,由于半径逐渐减小,由 ,ω逐渐增大,故C项正确。
答案:C1.线速度v与角速度ω的关系
(1)关系式:v=ωr。
(2)理解:
①当半径一定时,线速度的大小与角速度成正比。
②当角速度一定时,线速度的大小与半径成正比。
③当线速度一定时,半径与角速度成反比。 4.频率f与角速度ω、线速度v的关系
ω=2πf,v=2πfr。
5.频率f与转速n的关系
f=n(n的单位必须用r/s)。
6.角速度与转速的关系
做圆周运动的物体每转过一圈转过的角度为2π,所以ω=2πn。(n的单位r/s)[名师点睛] 1.2010年温哥华冬奥会双人滑比赛中,申雪、赵宏博拿到中国花样滑冰史上首枚冬奥会金牌,如图5-4-2所示,赵宏博(男)以自己为转轴拉着申雪(女)做匀速圆周运动,转速为30 r/min。申雪的脚到转轴的距离为1.6 m。求:
(1)申雪做匀速圆周运动的角速度;
(2)申雪的脚运动速度的大小。图5-4-2 [解析] (1)转动转速n=30 r/min=0.5 r/s
角速度ω=2π·n=2π×0.5 rad/s=π rad/s。
(2)申雪的脚做圆周运动的半径r=1.6 m,所以她的脚的运动速度大小v=ωr=π×1.6 m/s≈5.0 m/s。
[答案] (1)π rad/s (2)5.0 m/s 在讨论v、ω、r三者间的关系时,应先确保一个量不变,再确定另外两个量间的正、反比例关系。图5-4-3图5-4-4图5-4-5 [名师点睛] 在处理传动装置中各物理量间的关系时,首先确定是皮带、齿轮传动还是同轴转动,即确定v、ω中的不变量,从而确定其他各量的变化情况。 2.如图5-4-6所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB。若皮带不打滑,求A、B、C三轮边缘上a、b、c三点的角速度之比和线速度之比。图5-4-6[思路点拨] 解答本题时可按以下思路分析: [解析] A、B两轮通过皮带传动,皮带不打滑,则A、B两轮边缘的线速度大小相等,
即va=vb或va∶vb=1∶1 ①
由v=ωr得ωa∶ωb=rB∶rA=1∶2 ②
B、C两轮固定在一起绕同一轴转动,则B、C两轮的角 速度相等,即ωb=ωc或ωb∶ωc=1∶1 ③
由v=ωr得vb∶vc=rB∶rC=1∶2 ④
由②③得ωa∶ωb∶ωc=1∶2∶2,
由①④得va∶vb∶vc=1∶1∶2。
[答案] 1∶2∶2 1∶1∶2 解决传动问题时应明确装置的特点:
(1)同轴传动的物体上各点的角速度、转速和周期相等,但在同一轮上半径不同的各点线速度不同。
(2)皮带传动(皮带不打滑)中与皮带接触的两轮边缘上各点(或啮合的齿轮边缘的各点)的线速度大小相同,角速度与半径有关。解析:只有当ω一定时,线速度v才与轨道半径r成正比,所以A错误。同理v一定时,角速度ω才与轨道半径r成反比,所以B错误。在用转速或周期表示角速度时,角速度与转速成正比,与周期成反比,故C、D正确。
答案:CD2.(对应要点一)教师在黑板上画圆,圆规脚之间的距离是
25 cm,他保持这个距离不变,让粉笔在黑板上匀速的画了一个圆,粉笔的线速度是2.5 m/s。关于粉笔的运动,有下列说法:
①角速度是0.1 rad/s;②角速度是10 rad/s;③周期是
10 s;④周期是0.628 s;⑤频率是10 Hz;⑥频率是
1.59 Hz;⑦转速小于2 r/s;⑧转速大于2 r/s。下列哪个选项中的结果是全部正确的 ( )
A.①③⑤⑦ B.②④⑥⑧
C.②④⑥⑦ D.①③⑤⑧答案:C3.(对应要点二)某变速箱中有甲、乙、丙三个齿轮,如图5
-4-7所示,其半径分别为r1、r2、r3,若甲轮的角速度为ω,则丙轮的角速度为 ( )图5-4-7答案:A4.(对应要点二)如图5-4-8所示,圆环以
过其直径的直线AB为轴匀速转动。已知其半径R=0.5 m,周期T=4 s,求环上P点和Q点的角速度和线速度大小。图5-4-8答案:ωP=ωQ=1.57 rad/s
vP≈0.39 m/s vQ≈0.68 m/s
点击下图进入“课下作业综合提升”
·一点通要点一要点二第4节创新演练
·大冲关随堂检测归纳小结课下作业综合提升1. 理解匀速圆周运动的概念,知道匀
速圆周运动是变速运动。
2.理解匀速圆周运动的线速度和角速
度、周期、转速等描述圆周运动快
慢的概念。
3.掌握线速度、角速度、周期和频率
间的关系。[读教材·填要点]1.描述圆周运动的物理量
(1)圆周运动:物体沿着 的运动。
(2)描述圆周运动的物理量及相互关系圆周垂直相切转动快慢运动一周圈数标量标量矢量m/srad/ssr/s r/min [关键一点] 注意区别角速度的单位rad/s和转速的单位r/s,分别表示每秒转过的角度和圈数。2.匀速圆周运动
(1)定义:线速度的大小处处 的圆周运动。
(2)特点:
①线速度大小 ,方向 ,是一种 运动。
②角速度 。
③转速、 不变。相等不变时刻改变变速不变周期[试身手·夯基础]1.下列关于匀速圆周运动的说法中,正确的是 ( )
A.是线速度不变的运动
B.是角速度不变的运动
C.是角速度不断变化的运动
D.是相对圆心位移不变的运动
解析:匀速圆周运动,角速度保持不变,线速度大小保持不变,方向时刻变化,A、C错误,B正确;相对圆心的位移大小不变,方向时刻变化,D错误。
答案:B2.一质点做匀速圆周运动,其线速度大小为4 m/s,
转动周期为2 s,则不正确的是 ( )
A.角速度为0.5 rad/s
B.转速为0.5 r/s
C.运动轨迹的半径为1.27 m
D.频率为 Hz.答案:A3.质点做匀速圆周运动,则:
①在任何相等的时间里,质点的位移都相等
②在任何相等的时间里,质点通过的路程都相等
③在任何相等的时间里,质点运动的平均速度都相同
④在任何相等的时间里,连接质点和圆心的半径转过的角度都相等
以上说法中正确的是 ( )
A.①② B.③④
C.①③ D.②④解析:匀速圆周运动是变速运动,故在相等的时间内通过的路程相等,但位移不等,故①错,②正确。因为做匀速圆周运动的角速度不变,故④正确。平均速度是位移与时间的比值,所以③错。
答案:D4.光滑的水平面上固定着一个螺旋形光
滑轨道,俯视如图5-4-1所示。一个小球以一定速度沿轨道切线方向进入轨道,小球从进入轨道直到到达螺旋形中央区的时间内,关于小球运动的角速度和线速度大小变化的说法正确的是 ( )
A.增大、减小 B.不变、不变
C.增大、不变 D.减小、减小图5-4-1解析:由于轨道是光滑的,小球运动的线速度大小不变,由于半径逐渐减小,由 ,ω逐渐增大,故C项正确。
答案:C1.线速度v与角速度ω的关系
(1)关系式:v=ωr。
(2)理解:
①当半径一定时,线速度的大小与角速度成正比。
②当角速度一定时,线速度的大小与半径成正比。
③当线速度一定时,半径与角速度成反比。 4.频率f与角速度ω、线速度v的关系
ω=2πf,v=2πfr。
5.频率f与转速n的关系
f=n(n的单位必须用r/s)。
6.角速度与转速的关系
做圆周运动的物体每转过一圈转过的角度为2π,所以ω=2πn。(n的单位r/s)[名师点睛] 1.2010年温哥华冬奥会双人滑比赛中,申雪、赵宏博拿到中国花样滑冰史上首枚冬奥会金牌,如图5-4-2所示,赵宏博(男)以自己为转轴拉着申雪(女)做匀速圆周运动,转速为30 r/min。申雪的脚到转轴的距离为1.6 m。求:
(1)申雪做匀速圆周运动的角速度;
(2)申雪的脚运动速度的大小。图5-4-2 [解析] (1)转动转速n=30 r/min=0.5 r/s
角速度ω=2π·n=2π×0.5 rad/s=π rad/s。
(2)申雪的脚做圆周运动的半径r=1.6 m,所以她的脚的运动速度大小v=ωr=π×1.6 m/s≈5.0 m/s。
[答案] (1)π rad/s (2)5.0 m/s 在讨论v、ω、r三者间的关系时,应先确保一个量不变,再确定另外两个量间的正、反比例关系。图5-4-3图5-4-4图5-4-5 [名师点睛] 在处理传动装置中各物理量间的关系时,首先确定是皮带、齿轮传动还是同轴转动,即确定v、ω中的不变量,从而确定其他各量的变化情况。 2.如图5-4-6所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB。若皮带不打滑,求A、B、C三轮边缘上a、b、c三点的角速度之比和线速度之比。图5-4-6[思路点拨] 解答本题时可按以下思路分析: [解析] A、B两轮通过皮带传动,皮带不打滑,则A、B两轮边缘的线速度大小相等,
即va=vb或va∶vb=1∶1 ①
由v=ωr得ωa∶ωb=rB∶rA=1∶2 ②
B、C两轮固定在一起绕同一轴转动,则B、C两轮的角 速度相等,即ωb=ωc或ωb∶ωc=1∶1 ③
由v=ωr得vb∶vc=rB∶rC=1∶2 ④
由②③得ωa∶ωb∶ωc=1∶2∶2,
由①④得va∶vb∶vc=1∶1∶2。
[答案] 1∶2∶2 1∶1∶2 解决传动问题时应明确装置的特点:
(1)同轴传动的物体上各点的角速度、转速和周期相等,但在同一轮上半径不同的各点线速度不同。
(2)皮带传动(皮带不打滑)中与皮带接触的两轮边缘上各点(或啮合的齿轮边缘的各点)的线速度大小相同,角速度与半径有关。解析:只有当ω一定时,线速度v才与轨道半径r成正比,所以A错误。同理v一定时,角速度ω才与轨道半径r成反比,所以B错误。在用转速或周期表示角速度时,角速度与转速成正比,与周期成反比,故C、D正确。
答案:CD2.(对应要点一)教师在黑板上画圆,圆规脚之间的距离是
25 cm,他保持这个距离不变,让粉笔在黑板上匀速的画了一个圆,粉笔的线速度是2.5 m/s。关于粉笔的运动,有下列说法:
①角速度是0.1 rad/s;②角速度是10 rad/s;③周期是
10 s;④周期是0.628 s;⑤频率是10 Hz;⑥频率是
1.59 Hz;⑦转速小于2 r/s;⑧转速大于2 r/s。下列哪个选项中的结果是全部正确的 ( )
A.①③⑤⑦ B.②④⑥⑧
C.②④⑥⑦ D.①③⑤⑧答案:C3.(对应要点二)某变速箱中有甲、乙、丙三个齿轮,如图5
-4-7所示,其半径分别为r1、r2、r3,若甲轮的角速度为ω,则丙轮的角速度为 ( )图5-4-7答案:A4.(对应要点二)如图5-4-8所示,圆环以
过其直径的直线AB为轴匀速转动。已知其半径R=0.5 m,周期T=4 s,求环上P点和Q点的角速度和线速度大小。图5-4-8答案:ωP=ωQ=1.57 rad/s
vP≈0.39 m/s vQ≈0.68 m/s
点击下图进入“课下作业综合提升”
