华东师大版八年级下册数学 19.2.1 菱形的性质 课件(共14张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.2.1 菱形的性质 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-13 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
菱形的性质
将一张矩形的纸对折再对折,然后沿着图中的斜线剪下,然后打开,你发现这是一个什么样的图形呢
探究活动1:动手做一做
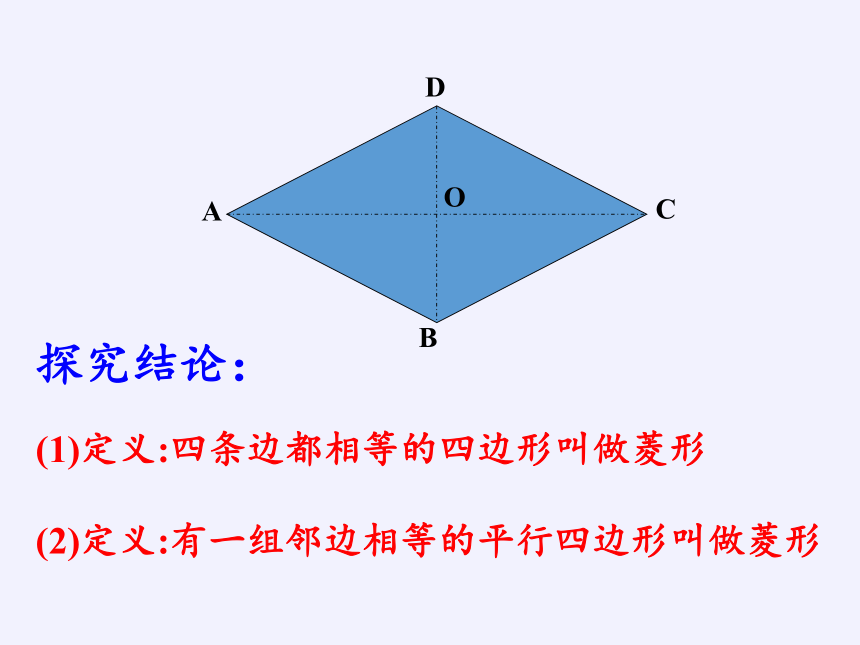
A
B
C
D
O
(1)定义:四条边都相等的四边形叫做菱形
(2)定义:有一组邻边相等的平行四边形叫做菱形
探究结论:
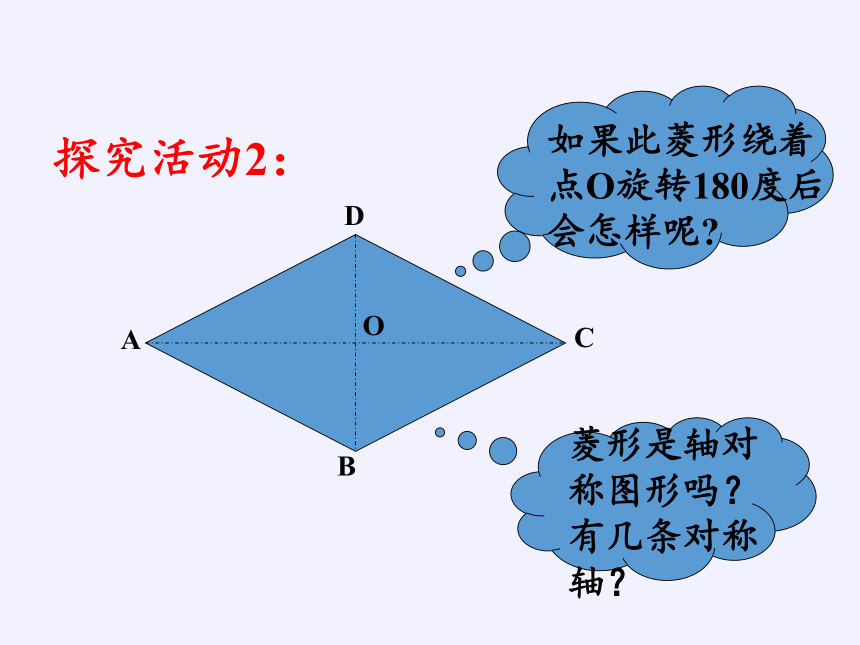
A
B
C
D
O
如果此菱形绕着
点O旋转180度后
会怎样呢
探究活动2:
菱形是轴对称图形吗?有几条对称轴?
我们发现:
菱形是轴对称图形,有两条对称轴;
它的对称轴是两条对角线所在的直线
我们发现:菱形是中心对称图形,
对称中心是两条对角线的交点。
探究结论:
菱形的性质
根据以上的探究,你能发现菱形
除了具备平行四边形的所有性质外,
它还有哪些特有的性质?
建议:可由菱形的边、对角线、角等方面考虑
1、菱形的四条边都相等
2、菱形的对角线互相垂直。
打好基础:
比一比,看谁的反应最快!
1、下列说法中错误的是( )
A、一组邻边相等的平行四边形是菱形;
B、对角线互相垂直的平行四边形是菱形;
C、对角线互相平分的四边形是菱形;
D、菱形的每一条对角线平分一组对角。
2、对于以下图形(1)矩形(2)等边三角形(3)平行四边形(4)菱形(5)圆(6)线段,既是轴对称图形又是中心对称图形的有( )
A、1个 B、2个 C、3个 D、4个
3、已知菱形的两条对角线长分别是10和24,则
菱形的周长为_____。
52
C
D
4、如图,矩形ABCD对角线相交于点O,CE∥BD,DE∥AC,DE和CE交于点E,四边形DOCE是菱形吗?请说明理由。
B
A
D
C
O
E
解:∵ DE∥AC,CE∥DB(已知)
∴四边形DOCE是平行四边形
(平行四边形的定义)
又∵四边形ABCD是矩形 ∴OD=OC(矩形对角线相等且平分)
∴四边形DOCE是菱形(一组邻边相等的平行四边形是菱形)
灵活运用、提升自我
5、如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。
A
C
B
D
解法一:在菱形ABCD中
∵AD//BC
∴∠B+∠BAD=180°
(两直线平行,同旁内角互补)
又∵ ∠BAD=2∠B(已知)
∴ ∠B + 2∠B=180°(等量代换)
∴ ∠B= 60°。
又∵AB=BC(菱形的四条边都相等)
∴ ΔABC是等边三角形
(有一个内角是60°的等腰三角形是等边三角形)
5:如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。
解法二:在菱形ABCD中,∠BAD=∠BCD
∵AC 平分∠BAD、∠BCD
(菱形的对角线平分一组内角)
∴∠1=∠2= ∠BAD
A
C
B
D
又∵ ∠BAD=2∠B(已知)
∴∠B= ∠BAD(等式的性质)
∴∠1=∠2 =∠B(等量代换)
∴AB=AC=BC(等角对等边)
即ΔABC是等边三角形
(三条边都相等的三角形是等边三角形)
1
2
菱形的应用非常广泛.
有一种衣帽架,可以根据需要将它伸缩,形成各种形状的菱形,固定在墙上,既美观又实用.
1、一个菱形的周长是20cm,它的一个内角
是60°,则此菱形较短对角线的长是_____。
课堂反馈
2、如图,菱形ABCD的对角线AC=12cm,
BD=16cm,AE⊥BC,求AE的长。
A
B
C
D
E
O
5cm
解:在菱形ABCD中,AC⊥BD,
OA=OC,OB=OD
∴OA=6cm,OB=8cm
∴AB=BC=10 cm
∵ AE⊥BC
∴ BC×AE= AC×OB
∴AE=9.6 cm
菱形 边 对称性 角 对角线
性 质
对边平行
四条边都相等
中心对称图形
轴对称图形
对角相等
对角线互相垂直
对角线互相平分
每一条对角线平分一组对角
大家一起来归纳:
作业:A组:P112练习1、B组P112练习:2、C组P112练习:3题.
谢 谢
菱形的性质
将一张矩形的纸对折再对折,然后沿着图中的斜线剪下,然后打开,你发现这是一个什么样的图形呢
探究活动1:动手做一做
A
B
C
D
O
(1)定义:四条边都相等的四边形叫做菱形
(2)定义:有一组邻边相等的平行四边形叫做菱形
探究结论:
A
B
C
D
O
如果此菱形绕着
点O旋转180度后
会怎样呢
探究活动2:
菱形是轴对称图形吗?有几条对称轴?
我们发现:
菱形是轴对称图形,有两条对称轴;
它的对称轴是两条对角线所在的直线
我们发现:菱形是中心对称图形,
对称中心是两条对角线的交点。
探究结论:
菱形的性质
根据以上的探究,你能发现菱形
除了具备平行四边形的所有性质外,
它还有哪些特有的性质?
建议:可由菱形的边、对角线、角等方面考虑
1、菱形的四条边都相等
2、菱形的对角线互相垂直。
打好基础:
比一比,看谁的反应最快!
1、下列说法中错误的是( )
A、一组邻边相等的平行四边形是菱形;
B、对角线互相垂直的平行四边形是菱形;
C、对角线互相平分的四边形是菱形;
D、菱形的每一条对角线平分一组对角。
2、对于以下图形(1)矩形(2)等边三角形(3)平行四边形(4)菱形(5)圆(6)线段,既是轴对称图形又是中心对称图形的有( )
A、1个 B、2个 C、3个 D、4个
3、已知菱形的两条对角线长分别是10和24,则
菱形的周长为_____。
52
C
D
4、如图,矩形ABCD对角线相交于点O,CE∥BD,DE∥AC,DE和CE交于点E,四边形DOCE是菱形吗?请说明理由。
B
A
D
C
O
E
解:∵ DE∥AC,CE∥DB(已知)
∴四边形DOCE是平行四边形
(平行四边形的定义)
又∵四边形ABCD是矩形 ∴OD=OC(矩形对角线相等且平分)
∴四边形DOCE是菱形(一组邻边相等的平行四边形是菱形)
灵活运用、提升自我
5、如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。
A
C
B
D
解法一:在菱形ABCD中
∵AD//BC
∴∠B+∠BAD=180°
(两直线平行,同旁内角互补)
又∵ ∠BAD=2∠B(已知)
∴ ∠B + 2∠B=180°(等量代换)
∴ ∠B= 60°。
又∵AB=BC(菱形的四条边都相等)
∴ ΔABC是等边三角形
(有一个内角是60°的等腰三角形是等边三角形)
5:如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。
解法二:在菱形ABCD中,∠BAD=∠BCD
∵AC 平分∠BAD、∠BCD
(菱形的对角线平分一组内角)
∴∠1=∠2= ∠BAD
A
C
B
D
又∵ ∠BAD=2∠B(已知)
∴∠B= ∠BAD(等式的性质)
∴∠1=∠2 =∠B(等量代换)
∴AB=AC=BC(等角对等边)
即ΔABC是等边三角形
(三条边都相等的三角形是等边三角形)
1
2
菱形的应用非常广泛.
有一种衣帽架,可以根据需要将它伸缩,形成各种形状的菱形,固定在墙上,既美观又实用.
1、一个菱形的周长是20cm,它的一个内角
是60°,则此菱形较短对角线的长是_____。
课堂反馈
2、如图,菱形ABCD的对角线AC=12cm,
BD=16cm,AE⊥BC,求AE的长。
A
B
C
D
E
O
5cm
解:在菱形ABCD中,AC⊥BD,
OA=OC,OB=OD
∴OA=6cm,OB=8cm
∴AB=BC=10 cm
∵ AE⊥BC
∴ BC×AE= AC×OB
∴AE=9.6 cm
菱形 边 对称性 角 对角线
性 质
对边平行
四条边都相等
中心对称图形
轴对称图形
对角相等
对角线互相垂直
对角线互相平分
每一条对角线平分一组对角
大家一起来归纳:
作业:A组:P112练习1、B组P112练习:2、C组P112练习:3题.
谢 谢
