华东师大版八年级下册数学 平行四边形复习 教案
文档属性
| 名称 | 华东师大版八年级下册数学 平行四边形复习 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 42.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-13 18:27:21 | ||
图片预览

文档简介
平行四边形复习
一、【复习目标】:
1.知道平行四边形与特殊平行四边形的关系;
2.引导学生通过练习回忆学过的知识,提高逻辑思维能力,掌握并能灵活利用平行四边形和特殊平行四边形的判定与性质.
二、【复习重难点】:
平行四边形与特殊平行四边形性质与判定的综合应用.
三、【复习过程】:
(—)【温故·习新】
问题1本章学习了哪些特殊的四边形?是按照什么次序学习的?请说说这些四边形是怎样形成的?
设计意图:引导学生有条理地回顾概念,并建立概念之间的联系。
(二)【研讨·拓展】
例1:在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,
求证: 四边形DEBF是平行四边形.
设计意图:引导学生多角度思考证明思路,巩固平行四边形的性质和判定。
师生活动:先有学生独立思考,然后由学生说思路,老师追问:你是怎样想到的?其他学生补充不同的方法,老师在黑板上整理出关键思路和步骤。
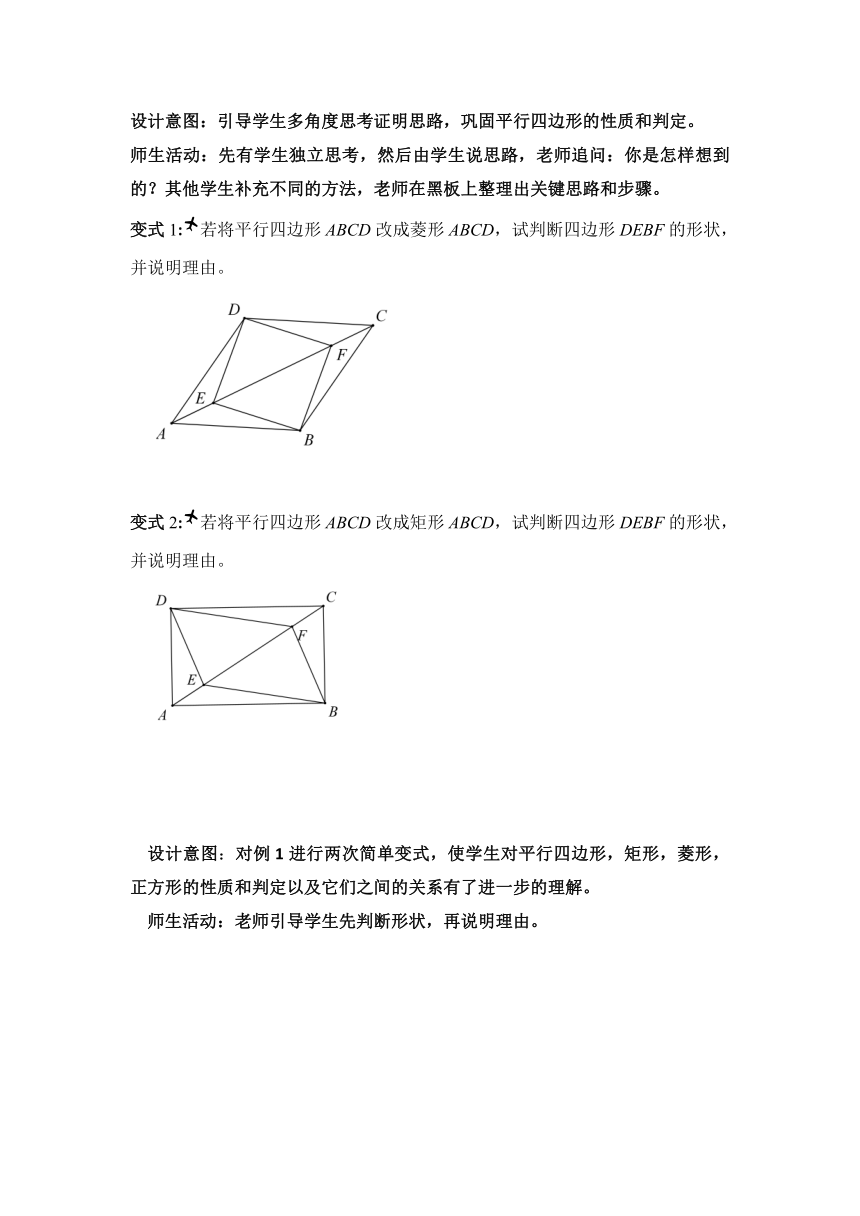
变式1:若将平行四边形ABCD改成菱形ABCD,试判断四边形DEBF的形状,并说明理由。
变式2:若将平行四边形ABCD改成矩形ABCD,试判断四边形DEBF的形状,并说明理由。
设计意图:对例1进行两次简单变式,使学生对平行四边形,矩形,菱形,正方形的性质和判定以及它们之间的关系有了进一步的理解。
师生活动:老师引导学生先判断形状,再说明理由。
例2如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AC⊥AB,则四边形ADCF是什么四边形?并证明你的结论.
(3)若AC=AB, 则四边形ADCF是什么四边形?并证明你的结论.
(4)若四边形ADCF为正方形,则△ABC需添加什么条件?
设计意图:通过一系列的改变条件和结论,使学生能较灵活地运用平行四边形,矩形,菱形,正方形的性质和判定解决有关问题。 并且等腰三角形三线合一,直角三角形的性质都得到合理的运用。
【反馈·提炼】
1 已知:如图,在ABCD中,AE=CF,EF与BD的交点为点O,
求证:OE=OF.
2如图所示,已知△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F,求证:四边形CFDE是正方形
3已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
【学习小结】
五、【课后作业】
一、【复习目标】:
1.知道平行四边形与特殊平行四边形的关系;
2.引导学生通过练习回忆学过的知识,提高逻辑思维能力,掌握并能灵活利用平行四边形和特殊平行四边形的判定与性质.
二、【复习重难点】:
平行四边形与特殊平行四边形性质与判定的综合应用.
三、【复习过程】:
(—)【温故·习新】
问题1本章学习了哪些特殊的四边形?是按照什么次序学习的?请说说这些四边形是怎样形成的?
设计意图:引导学生有条理地回顾概念,并建立概念之间的联系。
(二)【研讨·拓展】
例1:在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,
求证: 四边形DEBF是平行四边形.
设计意图:引导学生多角度思考证明思路,巩固平行四边形的性质和判定。
师生活动:先有学生独立思考,然后由学生说思路,老师追问:你是怎样想到的?其他学生补充不同的方法,老师在黑板上整理出关键思路和步骤。
变式1:若将平行四边形ABCD改成菱形ABCD,试判断四边形DEBF的形状,并说明理由。
变式2:若将平行四边形ABCD改成矩形ABCD,试判断四边形DEBF的形状,并说明理由。
设计意图:对例1进行两次简单变式,使学生对平行四边形,矩形,菱形,正方形的性质和判定以及它们之间的关系有了进一步的理解。
师生活动:老师引导学生先判断形状,再说明理由。
例2如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AC⊥AB,则四边形ADCF是什么四边形?并证明你的结论.
(3)若AC=AB, 则四边形ADCF是什么四边形?并证明你的结论.
(4)若四边形ADCF为正方形,则△ABC需添加什么条件?
设计意图:通过一系列的改变条件和结论,使学生能较灵活地运用平行四边形,矩形,菱形,正方形的性质和判定解决有关问题。 并且等腰三角形三线合一,直角三角形的性质都得到合理的运用。
【反馈·提炼】
1 已知:如图,在ABCD中,AE=CF,EF与BD的交点为点O,
求证:OE=OF.
2如图所示,已知△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F,求证:四边形CFDE是正方形
3已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
【学习小结】
五、【课后作业】
