2021-2022学年人教版数学七年级下册6.3 实数 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册6.3 实数 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 858.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 06:53:50 | ||
图片预览





文档简介
(共24张PPT)
6.3 实数
阅读课本53页,弄清以下概念:
无限不循环小数叫无理数.
1、什么是无理数?
无理数的两个条件:①无限,
②不循环。
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
2、我们学过哪些形式的无理数?
注意:带根号的数不一定是无理数
(如:2.1211221112222…)
(无限不循环小数)
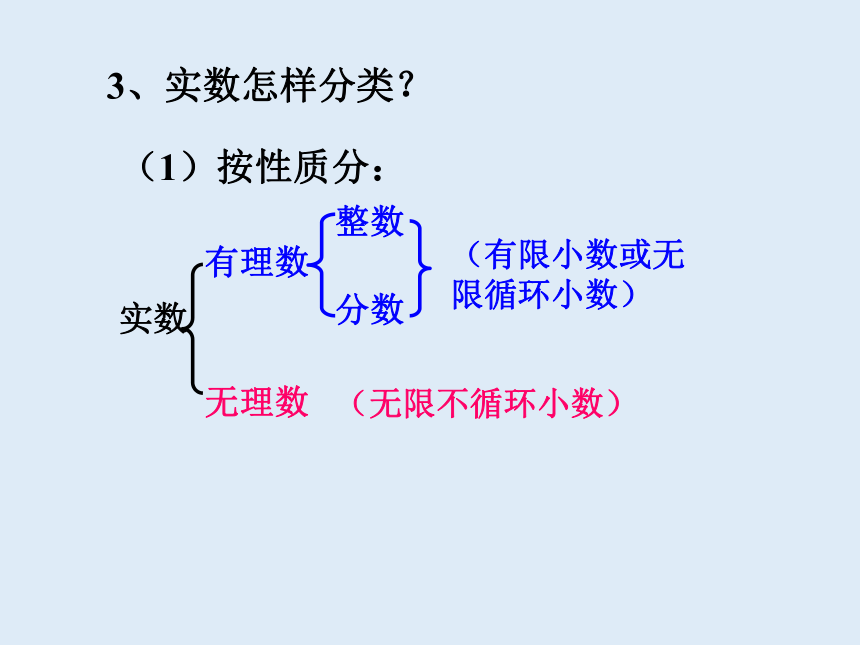
3、实数怎样分类?
无理数
有理数
实数
分数
整数
(有限小数或无限循环小数)
(1)按性质分:
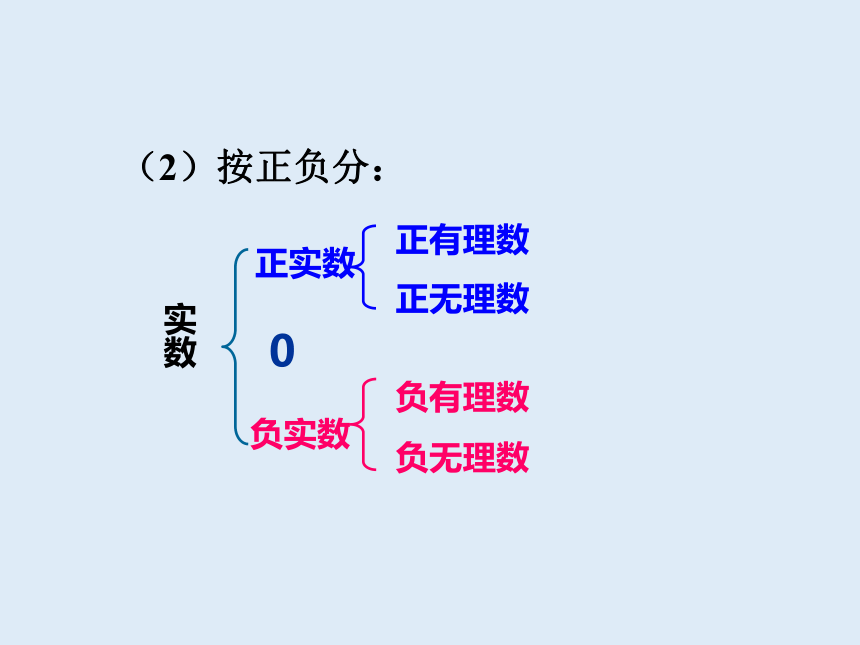
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
(2)按正负分:
把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
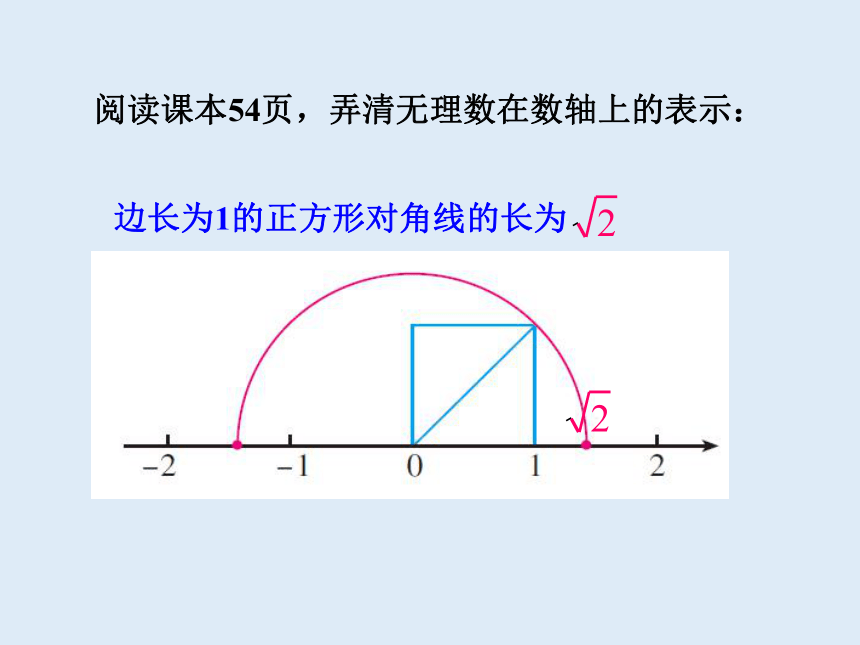
阅读课本54页,弄清无理数在数轴上的表示:
2
边长为1的正方形对角线的长为
2
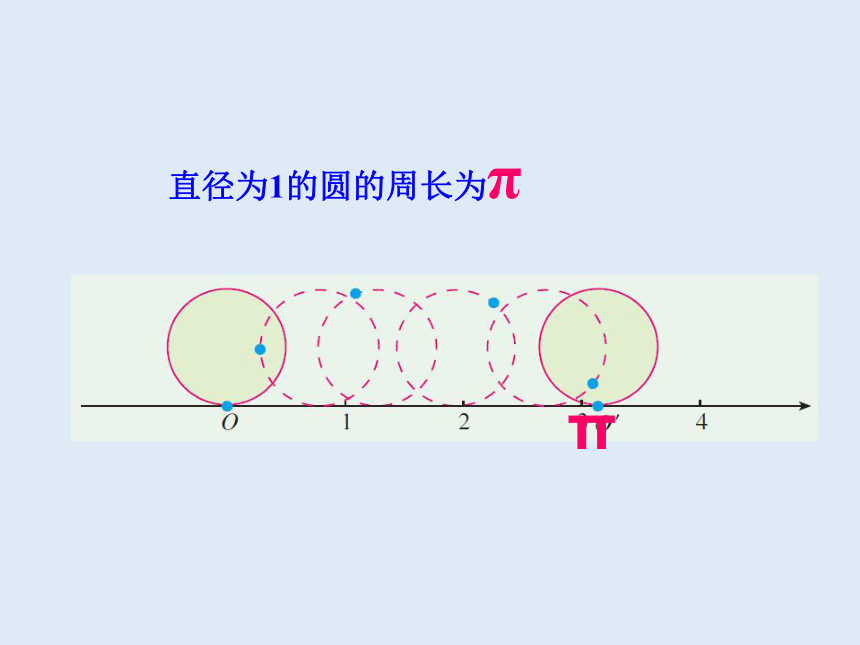
直径为1的圆的周长为π
π
归纳
数的范围从有理数抗充到实数后,
每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
实数与数轴上的点一一对应。
判断正误.
(1)无理数都是无限小数;( )
(2) 实数包括正实数、0、负实数;( )
(3)不带根号的数都是有理数;( )
(4)有理数都可以用数轴上的点表示,无理数也可以用数轴上的点表示。( )
√
√
×
×
强化训练
1、若无理数a满足:1<a<4,请写出两个你熟悉的无理数:_____,______.
2、判断下列说法是否正确:
(1)带根号的数是无理数;( )
(2)不带根号的数一定是有理数;( )
(3)负数没有立方根;( )
(4)-
是17的平方根.( )
×
×
×
√
练习1 下列各数中,哪些是有理数?哪些是无理数?
有理数
有理数
无理数
有理数
有理数
无理数
实数的性质
14
2022/3/13
15
知识回忆
只有符号不同的两个数,其中一个是另一个的相反数.
1、相反数
2、绝对值
数轴上表示数a的点到原点的距离叫做数a的绝对值,用︱a︱表示.
3、倒数
如果两个数的积是1,则这两个数互为倒数.
思考:无理数有相反数、绝对值或倒数吗?如何表示?
2022/3/13
16
有理数中的相反数、绝对值、倒数等概念对实数仍然适用.
如:
1. 相反数
2. 绝对值
数轴上一个数表示的点离开原点的距离
叫这个数的绝对值.
如:
3. 倒数
如果两个数的积等于1,这两个数叫互为倒数.
其中一个叫另一个的倒数.
一、实数的性质
如: 的倒数是
2022/3/13
17
的相反数是 ,
的相反数是 .
的相反数是 ,
-π的绝对值是 ,
= .
= ,
-π的绝对值是 ,
= .
= ,
2022/3/13
18
1.a是一个实数,实数a的相反数为-a.
2.①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③0的绝对值是0.
总结归纳
2022/3/13
19
例:求下列各数的相反数和绝对值:
解: 因为
所以, 的相反数分别为
由绝对值的意义得:
2022/3/13
20
当数从有理数扩充到实数以后,实数之间不仅可以进行加、减、乘、除、乘方运算,又增加了非负数的开平方运算,任意实数可以进行开立方运算.进行实数运算时,有理数的运算法则及性质等同样适用.
实数的运算顺序
(1)先算乘方和开方;
(2)再算乘除,最后算加减;
(3)如果有括号,则先进行括号里的运算.
二、实数的运算
2022/3/13
21
例: 计算下列各式的值:
反思总结:
你有什么收获?和同学交流一下
2022/3/13
22
2022/3/13
23
(2)注意两点:一是运算顺序;二是灵活运用运算律简化计算.
(1)实数的加、减、乘、除、乘方和开方运算:①减法变加法:减去一个数等于加上这个数的相
反数,即:a-b=a+(-b);
②除法变乘法:除以一个不等于0的数等于乘以这
个数的倒数,即a÷b=a×
课堂小结
谢谢倾听
2022/3/13
24
6.3 实数
阅读课本53页,弄清以下概念:
无限不循环小数叫无理数.
1、什么是无理数?
无理数的两个条件:①无限,
②不循环。
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
2、我们学过哪些形式的无理数?
注意:带根号的数不一定是无理数
(如:2.1211221112222…)
(无限不循环小数)
3、实数怎样分类?
无理数
有理数
实数
分数
整数
(有限小数或无限循环小数)
(1)按性质分:
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
(2)按正负分:
把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
阅读课本54页,弄清无理数在数轴上的表示:
2
边长为1的正方形对角线的长为
2
直径为1的圆的周长为π
π
归纳
数的范围从有理数抗充到实数后,
每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
实数与数轴上的点一一对应。
判断正误.
(1)无理数都是无限小数;( )
(2) 实数包括正实数、0、负实数;( )
(3)不带根号的数都是有理数;( )
(4)有理数都可以用数轴上的点表示,无理数也可以用数轴上的点表示。( )
√
√
×
×
强化训练
1、若无理数a满足:1<a<4,请写出两个你熟悉的无理数:_____,______.
2、判断下列说法是否正确:
(1)带根号的数是无理数;( )
(2)不带根号的数一定是有理数;( )
(3)负数没有立方根;( )
(4)-
是17的平方根.( )
×
×
×
√
练习1 下列各数中,哪些是有理数?哪些是无理数?
有理数
有理数
无理数
有理数
有理数
无理数
实数的性质
14
2022/3/13
15
知识回忆
只有符号不同的两个数,其中一个是另一个的相反数.
1、相反数
2、绝对值
数轴上表示数a的点到原点的距离叫做数a的绝对值,用︱a︱表示.
3、倒数
如果两个数的积是1,则这两个数互为倒数.
思考:无理数有相反数、绝对值或倒数吗?如何表示?
2022/3/13
16
有理数中的相反数、绝对值、倒数等概念对实数仍然适用.
如:
1. 相反数
2. 绝对值
数轴上一个数表示的点离开原点的距离
叫这个数的绝对值.
如:
3. 倒数
如果两个数的积等于1,这两个数叫互为倒数.
其中一个叫另一个的倒数.
一、实数的性质
如: 的倒数是
2022/3/13
17
的相反数是 ,
的相反数是 .
的相反数是 ,
-π的绝对值是 ,
= .
= ,
-π的绝对值是 ,
= .
= ,
2022/3/13
18
1.a是一个实数,实数a的相反数为-a.
2.①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③0的绝对值是0.
总结归纳
2022/3/13
19
例:求下列各数的相反数和绝对值:
解: 因为
所以, 的相反数分别为
由绝对值的意义得:
2022/3/13
20
当数从有理数扩充到实数以后,实数之间不仅可以进行加、减、乘、除、乘方运算,又增加了非负数的开平方运算,任意实数可以进行开立方运算.进行实数运算时,有理数的运算法则及性质等同样适用.
实数的运算顺序
(1)先算乘方和开方;
(2)再算乘除,最后算加减;
(3)如果有括号,则先进行括号里的运算.
二、实数的运算
2022/3/13
21
例: 计算下列各式的值:
反思总结:
你有什么收获?和同学交流一下
2022/3/13
22
2022/3/13
23
(2)注意两点:一是运算顺序;二是灵活运用运算律简化计算.
(1)实数的加、减、乘、除、乘方和开方运算:①减法变加法:减去一个数等于加上这个数的相
反数,即:a-b=a+(-b);
②除法变乘法:除以一个不等于0的数等于乘以这
个数的倒数,即a÷b=a×
课堂小结
谢谢倾听
2022/3/13
24
