高中数学人教A版(2019)必修第二册第十章验收检测卷B(Word含答案解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修第二册第十章验收检测卷B(Word含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 477.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 00:00:00 | ||
图片预览




文档简介
高中数学人教A版(2019) 必修第二册 第十章 验收检测卷
一、单选题
1.已知,,则事件与事件( )
A.互斥 B.对立 C.独立 D.以上均不正确
2.为了缓解道路拥堵,合理分配车流,有关部门对城市若干道路的流量情况展开调查.调查员甲经实地观察发现,道路K由于较为偏僻,在分钟内出现车辆的概率仅为 .若车辆在任何时刻出现的概率都是独立的,则甲观察分钟就能发现车辆的概率约为( )
A.0.3 B.0.4 C.0.5 D.0.6
3.2021年世界园艺博览会于2021年4月到10月在江苏省扬州市举行,“花艺园”的某个部位摆放了10盆牡丹花,编号分别为0,1,2,3,……,9,若从任取1盆,则编号“大于5”的概率是( )
A. B. C. D.
4.已知A与是互斥事件,且,,则等于( )
A.0.1 B.0.3 C.0.4 D.0.8
5.某学校食堂推出两款优惠套餐,甲、乙、丙三位同学选择同一款套餐的概率为( )
A. B. C. D.
6.在这个热“晴”似火的7月,多地持续高温,某市气象局将发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温37摄氏度以上的概率是.某人用计算机生成了20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用0,1,2,3,4表示高温橙色预警,用5,6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )A. B. C. D.
7.下列问题中不是组合问题的是( )
A.10个朋友聚会,每两人握手一次,一共握手多少次
B.平面上有2020个不同点,它们中任意三点不共线,连接任意两点可以构成多少条直线
C.集合的含有三个元素的子集有多少个
D.从高二(6)班的50名学生中选出2名学生分别参加校庆晚会的独唱、独舞节目,有多少种选法
8.关于圆周率,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计的值:先请100名同学每人随机写下一个,都小于1的正实数对;再统计两数能与1构成钝角三角形三边的数对的个数;最后再根据统计数估计的值,假如某次统计结果是,那么本次实验可以估计的值为( ).
A. B. C. D.
二、多选题
9.袋中装有形状完全相同的个白球和个黑球,从中一次摸出个球,下列事件是互斥事件的是( )
A.摸出三个白球事件和摸出三个黑球事件
B.恰好有一黑球事件和都是黑球事件
C.至少一个黑球事件和至多一个白球事件
D.至少一个黑球事件和全是白球事件
10.甲、乙两人下棋,和棋的概率为,乙获胜的概率为,则下列说法错误的是( )
A.甲获胜的概率是 B.甲不输的概率是
C.乙输的概率是 D.乙不输的概率是
11.(多选)在一次随机试验中,,,,是彼此互斥的事件,且是必然事件,则下列说法正确的是( )
A.与是互斥事件,也是对立事件
B.与是互斥事件,但不是对立事件
C.与是互斥事件,但不是对立事件
D.与是互斥事件,也是对立事件
12.若,,,则事件与的关系错误是( )
A.事件与互斥 B.事件与对立
C.事件与相互独立 D.事件与既互斥又独立
三、填空题
13.世卫组织就新型冠状病毒感染的肺炎疫情称,新型病毒可能造成“持续人传人”.通俗点说就是存在A传B,B又传C,C又传D,这就是“持续人传人”.那么A、B、C就会被称为第一代、第二代、第三代传播者.假设一个身体健康的人被第一代、第二代、第三代传播者感染的概率分别为0.9,0.8,0.7,健康的小明参加了一次多人宴会,事后知道,参加宴会的人有5名第一代传播者,3名第二代传播者,2名第三代传播者,试计算,小明参加聚会,仅和感染的10个人其中一个接触,感染的概率有多大________.
14.有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是______结果用最简分数表示.
15.从3名男生和4名女生中选3人参加志愿者活动,则选到的志愿者中既有男生又有女生的不同选法共有__________种.(用数字作答)
16.从一批羽毛球产品中任取一个,质量小于4.8 g的概率为0.3,质量小于4.85 g的概率为0.32,那么质量在[4.8,4.85)(g)范围内的概率是________.
四、解答题
17.在标准化考试中既有单选题又有多选题,多选题是从A, B, C, D四个选项中选出所有正确的答案(四个选项中至少有两个选项是正确的).同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?
18.某手机厂家生产、、三种型号的手机,每种型号手机又分为标准版和版两个版本,某月的产量(单位:部)如表:
型号 型号 型号
标准版 200 650
版 300 350 600
该厂质检部门采用分层随机抽样的方法从这个月生产的手机中抽取100部,其中型号手机20部.
(1)求的值;
(2)在型号手机中采用分层随机抽样的方法抽取5部手机,再从这5部手机中任意抽取2部,求至多有1部手机为版的概率;
(3)该手机厂家所在城市的质量技术监督部门从型号手机中采用简单随机抽样的方法抽取了8部手机,经相关技术部门进行检测,这8部手机的综合质量得分分别为9.2、8.8、8.5、9.0、9.3、9.2、8.6、9.4(满分均为10分),将这8部手机的得分看成一个整体,若这8部手机中,与该整体平均得分之差的绝对值不超过0.3的概率低于0.65时,则该型号的手机不能投入市场.请通过计算判断型号手机是否能投入市场?
19.甲、乙两个乒乓球选手进行比赛,他们每一局获胜的概率均为,且每局比赛互补影响,规定“七局四胜”,即先赢四局者胜,若已知甲先赢了前两局,求:
(1)乙取胜的概率;
(2)设比赛局数为,求的分布列.
20.某单位一办公室现安排4个人去参加植树活动,该活动有甲、乙两个地点可供选择.约定:每个人通过掷一枚质地均匀的骰子决定自己去哪个地点植树,掷出点数为1或2的人去甲地,掷出点数大于2的人去乙地.
(1)求这4个人中恰有2人去甲地的概率;
(2)求这4个人中去甲地的人数大于去乙地的人数的概率;
(3)用X,Y分别表示这4个人中去甲、乙两地的人数,记,求随机变量的分布列与数学期望.
21.设某工厂有两个车间生产同型号家用电器,第一车间的次品率为0.15,第二车间的次品率为0.12,两个车间的成品都混合堆放在一个仓库.假设第一车间和第二车间生产的成品比例为2:3,今有一客户从成品仓库中随机提一台产品,求该产品合格的概率.
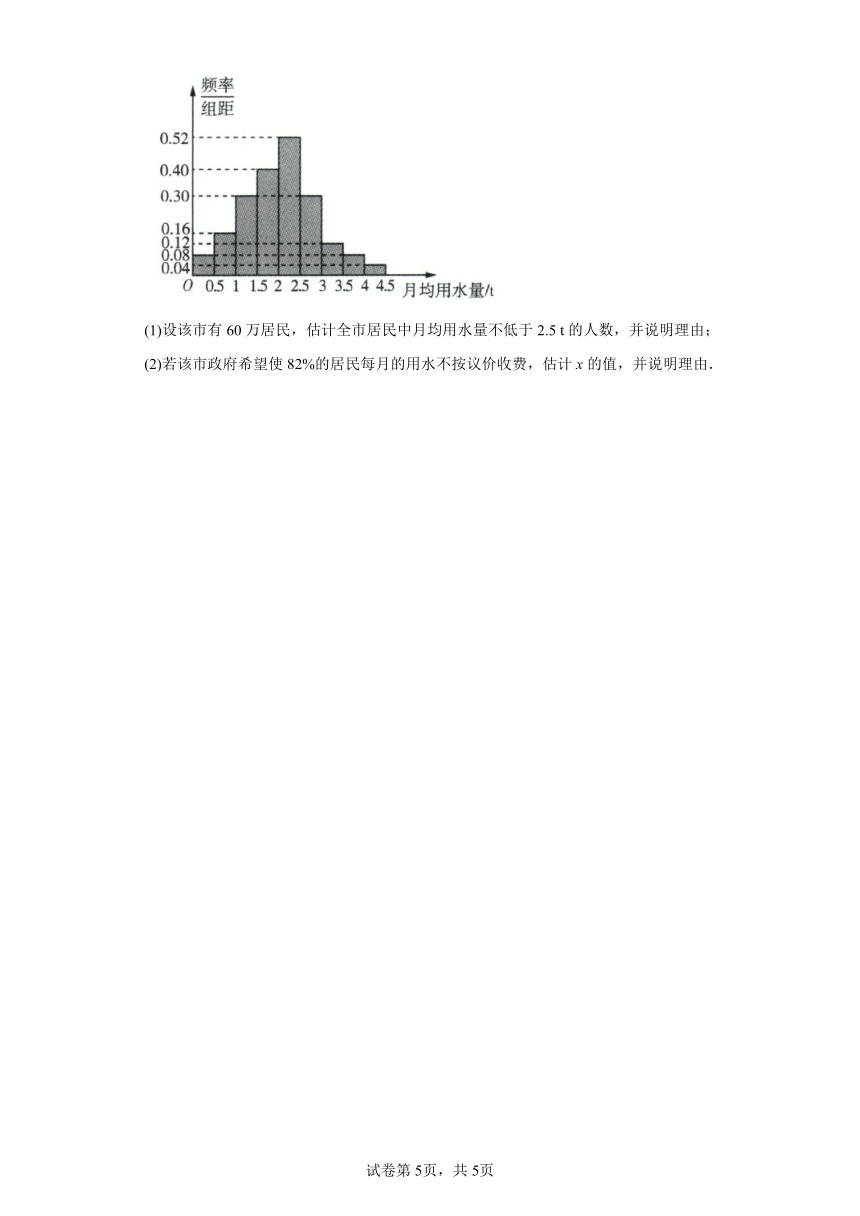
22.“水是生命之源”,但是据科学界统计,可用淡水资源仅占地球储水总量的2.8%,全世界近80%人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(单位:t):一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过随机抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照,,,分成9组,制成了如图所示的频率分布直方图.
(1)设该市有60万居民,估计全市居民中月均用水量不低于2.5 t的人数,并说明理由;
(2)若该市政府希望使82%的居民每月的用水不按议价收费,估计x的值,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
利用对立事件概率计算及条件概率公式推导出即可得解.
【详解】
依题意,,则,即,
于是得,所以事件与事件独立.
故选:C
2.B
【解析】
【分析】
由于车辆在任何时刻出现的概率都是独立的,所以观察到与观察不到的概率相等,又分钟小于分钟,根据题意,即可求出结果.
【详解】
由题意可知,在分钟内出现车辆的概率仅为,30分钟内不出现车辆的概率为0.2,30分钟内不出现车辆即是连续三个10分钟不出现车辆,即约等于0.6,
所以观察分钟就能发现车辆的概率约为.
故选:B.
3.B
【解析】
【分析】
设编号为随机变量,结合题设可得其各可能值的对应概率,再应用互斥事件概率的加法公式求即可.
【详解】
设任取1盆的编号为随机变量,
∴的可能取值为0,1,2,……,9,且,
∴.
故选:B.
4.D
【解析】
【分析】
根据互斥事件概率的加法关系即可求解.
【详解】
由题:A,B是互斥事件,
所以,
且,,
则.
故选:D
5.C
【解析】
【分析】
根据题意求得基本事件的总数,再利用列举法求得所求事件包含的基本事件的个数,利用古典摡型的概率计算公式,即可求解.
【详解】
设两款优惠套餐分别为A,B,甲乙丙三位同学,每人都有两种选法,
由分步计数原理,可得甲乙丙三位同学共有种不同的选法,
其中甲、乙、丙三位同学选择同一款套餐包括:有2种选法,
根据古典摡型的概率计算公式,可得概率为.
故选:C.
6.A
【解析】
【分析】
运用列举法得,今后的3天中恰有2天发布高温橙色预警信号的随机数有12个,由古典概型公式可得选项.
【详解】
解:今后的3天中恰有2天发布高温橙色预警信号的随机数有12个,分别为:
116, 812, 730, 452, 125, 217, 109, 361, 284, 147, 318, 027,
则今后的3天中恰有2天发布高温橙色预警信号的概率估计是:,
故选:A.
7.D
【解析】
【分析】
因为组合是与顺序无关的,所以A,B,C都是组合问题,D是排列问题.
【详解】
选项A中 ,是组合问题;选项B中,是组合问题;选项C中,是组合问题;选项D中 有顺序,是排列问题.
故选:D.
8.C
【解析】
【分析】
根据约束条件画出可行域,得到面积,根据几何概型得到答案.
【详解】
∵而满足构成钝角三角形,则需画出图像:
弓形面积:,∴.
故选
【点睛】
本题考查了几何概型,画出图像是解题的关键,意在考查学生的综合应用能力.
9.ABD
【解析】
【分析】
根据互斥事件的定义可判断各选项的正误,从而可得正确的选项.
【详解】
对于A,摸出三个白球事件和摸出三个黑球事件不可能同时发生,故它们为互斥事件,故A正确.
对于B,恰好有一黑球事件和都是黑球事件不可能同时发生,故它们为互斥事件,故B正确.
对于C,比如三个球中两个黑球和1个白球,则至少一个黑球事件和至多一个白球事件可同时发生,故C错误.
对于D,至少一个黑球事件和全是白球事件也不可能同时发生,故D正确.
故选:ABD.
10.BCD
【解析】
【分析】
由对立事件、互斥事件、并事件的概率计算公式代入计算,对选项逐一判断.
【详解】
“甲获胜”是“和棋或乙获胜”的对立事件,所以“甲获胜”的概率是,故A正确;设甲不输为事件A,则事件A是“甲获胜”和“和棋”这两个互斥事件的并事件,所以,故B错误;“乙输”的概率即“甲获胜”的概率,为,故C错误;设乙不输为事件B,则事件B是“乙获胜”和“和棋”这两个互斥事件的并事件,所以,故D错误;
故选:BCD
11.BD
【解析】
【分析】
根据互斥事件和对立事件的定义进行判断即可.
【详解】
由于,,,彼此互斥,且是必然事件,故事件的关系如图所示.
由图可知,任何一个事件与其余三个事件的并事件互为对立事件,任何两个事件的并事件与其余两个事件中任何一个是互斥事件,但不是对立事件,任何两个事件的并事件与其余两个事件的并事件互为对立事件,
故选:BD
12.ABD
【解析】
【分析】
计算得出,由此可得出结论.
【详解】
由题意可得,因为,,所以,,
故事件与相互独立.
故选:ABD.
13.
【解析】
【分析】
求出小明与第一代、第二代、第三代传播者接触的概率,利用独立事件、互斥事件的概率公式求解即可.
【详解】
设事件,,为第一代、第二代、第三代传播者接触,
事件为小明被感染,由已知得:
(A),(B),(C),,,,
(D)(A)(B)(C)
.
小明参加聚会,仅和感染的10个人其中一个接触,感染的概率为0.83.
故答案为:0.83.
【点睛】
本题考查概率的求法,考查独立事件、互斥事件的概率公式以及条件概率的性质等基础知识,考查运算求解能力,是基础题.
14.
【解析】
【分析】
求出所有事件的总数,求出三个砝码的总质量为9克的事件总数,然后用古典概率公式求解概率即可.
【详解】
编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,
从中随机选取三个,所有的事件总数为:,
这三个砝码的总质量为9克的事件只有:5,3,1或5,2,2两种情况,
所以:这三个砝码的总质量为9克的概率是:,
故答案为:.
15.30
【解析】
【分析】
由题可得共有种不同选法,然后计算3人都是男生或都是女生的选法,即求.
【详解】
从3名男生和4名女生中选3人参加志愿者活动,共有种不同选法,
其中3人都是男生或都是女生的选法有种,
所以选到的志愿者中既有男生又有女生的不同选法共有种.
故答案为:30.
16.0.02
【解析】
【分析】
把质量小于4.85 g的事件分拆成质量小于4.8 g的事件与质量在[4.8,4.85)(g)范围内的事件的和,再利用概率的加法公式即可得解.
【详解】
从羽毛球产品中任取一个,A={质量小于4.8 g},B={质量在[4.8,4.85)(g)范围内},C={质量小于4.85 g},
事件A与B互斥,且C=A+B,而P(A)=0.3,P(C)=0.32,
由P(C)=P(A+B)=P(A)+P(B),得P(B)=P(C)-P(A)=0.32-0.3=0.02,
所以质量在[4.8,4.85)(g)范围内的概率是0.02.
故答案为:0.02
17.答案见解析
【解析】
【分析】
列出基本事件个数,利用古典概型的概率计算公式求出概率即可得出答案.
【详解】
易知单选题猜对的概率为,对于多选题,
试验的样本空间为
{AB, AC, AD, BC, BD, CD, ABC, ABD, ACD, BCD, ABCD},
样本点共有11个,而正确答案只有1个,因此猜对的概率为 ,
因为<,即多选题猜对的概率小,所以多选题更难猜对.
18.(1)400
(2)
(3)该型号的手机不能投入市场
【解析】
【分析】
(1)根据分成抽样的知识,利用比例列方程,化简求得.
(2)结合古典概型概率计算公式,计算出所求概率.
(3)先求得总体平均分,然后求得“这8部手机中,与该整体平均得分之差的绝对值不超过0.3的概率”,进而作出判断.
(1)
由分层抽样的性质得:
,
解得.
(2)
在型号手机中采用分层随机抽样的方法抽取5部手机,
则标准版抽取部,版抽取部,
再从这5部手机中任意抽取2部,
基本事件总数,
至多有1部手机为版包含的基本事件个数,
至多有1部手机为版的概率.
(3)
这8部手机的综合质量得分分别为9.2、8.8、8.5、9.0、9.3、9.2、8.6、9.4(满分均为10分),
将这8部手机的得分看成一个整体,
该整体平均得分为,
这8部手机中,与该整体平均得分之差的绝对值不超过0.3的综合质量得分有:
9.2、8.8、9.0、9.3、9.2,共5个,
这8部手机中,与该整体平均得分之差的绝对值不超过0.3的概率,
该型号的手机不能投入市场.
19.(1)
(2)分布列见解析
【解析】
【分析】
(1)当甲先胜了前两局时,乙取胜的性质有两种:第一种是乙连胜三局,第二种是在第三局到第六局,乙胜了三局,第七局乙胜,求出两种情况的概率和可得答案;
(2)求出的可能取值和对应的概率可得答案.
(1)
当甲先胜了前两局时,乙取胜的性质有两种:第一种是乙连胜三局,第二种是在第三局到第六局,乙胜了三局,第七局乙胜,
第一种情况下乙取胜的概率为:,
第二种情况下乙取值的概率为:,
甲先赢了前两局,乙取胜的概率为
.
(2)
由已知得的可能取值为4,5,6,7,
,
,
,
,
的分布列为:
4 5 6 7
20.(1)
(2)
(3)分布列见解析,
【解析】
【分析】
(1)利用独立事件乘法公式求4个人中恰有2人去甲地的概率;
(2)由(1)知:4个人中恰有3或4人去甲地,应用互斥事件的加法公式,概率即可;
(3)根据(1)确定的可能值,并求出对应的概率,进而写出分布列,根据分布列求期望即可.
(1)
依题意知,这4个人中每个人去甲地的概率为,去乙地的概率为.
设“这4个人中恰有i人去甲地”为事件,则.
∴这4个人中恰有2人去甲地的概率.
(2)
设“这4个人中去甲地的人数大于去乙地的人数”为事件B,则.
由于与互斥,故.
∴这4个人中去甲地的人数大于去乙地的人数的概率为.
(3)
的所有可能的取值为0,2,4,由于与互斥,与互斥,
故,,.
∴的分布列为
0 2 4
P
故.
21.0.868
【解析】
【分析】
利用相互独立事件概率乘法公式能求出该产品合格的概率.
【详解】
设某工厂有两个车间生产同型号家用电器,第一车间的次品率为0.15,第二车间的次品率为0.12,
两个车间的成品都混合堆放在一个仓库,假设第1,2车间生产的成品比例为,
今有一客户从成品仓库中随机提一台产品,
则该产品合格的概率为.
该产品合格的概率为0.868.
22.(1)估计全市居民中月均用水量不低于2.5 t的人数为(万),理由见解析
(2)估计x的值为2.8,理由见解析
【解析】
【分析】
(1)先根据频率分布直方图求出月均用水量不低于2.5 t人数所占百分比,再乘以全市居民人数即可;
(2)先通过88%的居民月均用水量小于3 t得到,再根据计算即可.
(1)
由题图可知,不低于2.5 t人数所占百分比为,
所以估计全市居民中月均用水量不低于2.5 t的人数为(万).
(2)
由(1)可知,月均用水量小于2.5 t的居民人数所占百分比为73%,
即73%的居民月均用水量小于2.5 t,
则73%+
所以88%的居民月均用水量小于3 t,故,
所以.
故估计x的值为2.8.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知,,则事件与事件( )
A.互斥 B.对立 C.独立 D.以上均不正确
2.为了缓解道路拥堵,合理分配车流,有关部门对城市若干道路的流量情况展开调查.调查员甲经实地观察发现,道路K由于较为偏僻,在分钟内出现车辆的概率仅为 .若车辆在任何时刻出现的概率都是独立的,则甲观察分钟就能发现车辆的概率约为( )
A.0.3 B.0.4 C.0.5 D.0.6
3.2021年世界园艺博览会于2021年4月到10月在江苏省扬州市举行,“花艺园”的某个部位摆放了10盆牡丹花,编号分别为0,1,2,3,……,9,若从任取1盆,则编号“大于5”的概率是( )
A. B. C. D.
4.已知A与是互斥事件,且,,则等于( )
A.0.1 B.0.3 C.0.4 D.0.8
5.某学校食堂推出两款优惠套餐,甲、乙、丙三位同学选择同一款套餐的概率为( )
A. B. C. D.
6.在这个热“晴”似火的7月,多地持续高温,某市气象局将发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温37摄氏度以上的概率是.某人用计算机生成了20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用0,1,2,3,4表示高温橙色预警,用5,6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )A. B. C. D.
7.下列问题中不是组合问题的是( )
A.10个朋友聚会,每两人握手一次,一共握手多少次
B.平面上有2020个不同点,它们中任意三点不共线,连接任意两点可以构成多少条直线
C.集合的含有三个元素的子集有多少个
D.从高二(6)班的50名学生中选出2名学生分别参加校庆晚会的独唱、独舞节目,有多少种选法
8.关于圆周率,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计的值:先请100名同学每人随机写下一个,都小于1的正实数对;再统计两数能与1构成钝角三角形三边的数对的个数;最后再根据统计数估计的值,假如某次统计结果是,那么本次实验可以估计的值为( ).
A. B. C. D.
二、多选题
9.袋中装有形状完全相同的个白球和个黑球,从中一次摸出个球,下列事件是互斥事件的是( )
A.摸出三个白球事件和摸出三个黑球事件
B.恰好有一黑球事件和都是黑球事件
C.至少一个黑球事件和至多一个白球事件
D.至少一个黑球事件和全是白球事件
10.甲、乙两人下棋,和棋的概率为,乙获胜的概率为,则下列说法错误的是( )
A.甲获胜的概率是 B.甲不输的概率是
C.乙输的概率是 D.乙不输的概率是
11.(多选)在一次随机试验中,,,,是彼此互斥的事件,且是必然事件,则下列说法正确的是( )
A.与是互斥事件,也是对立事件
B.与是互斥事件,但不是对立事件
C.与是互斥事件,但不是对立事件
D.与是互斥事件,也是对立事件
12.若,,,则事件与的关系错误是( )
A.事件与互斥 B.事件与对立
C.事件与相互独立 D.事件与既互斥又独立
三、填空题
13.世卫组织就新型冠状病毒感染的肺炎疫情称,新型病毒可能造成“持续人传人”.通俗点说就是存在A传B,B又传C,C又传D,这就是“持续人传人”.那么A、B、C就会被称为第一代、第二代、第三代传播者.假设一个身体健康的人被第一代、第二代、第三代传播者感染的概率分别为0.9,0.8,0.7,健康的小明参加了一次多人宴会,事后知道,参加宴会的人有5名第一代传播者,3名第二代传播者,2名第三代传播者,试计算,小明参加聚会,仅和感染的10个人其中一个接触,感染的概率有多大________.
14.有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是______结果用最简分数表示.
15.从3名男生和4名女生中选3人参加志愿者活动,则选到的志愿者中既有男生又有女生的不同选法共有__________种.(用数字作答)
16.从一批羽毛球产品中任取一个,质量小于4.8 g的概率为0.3,质量小于4.85 g的概率为0.32,那么质量在[4.8,4.85)(g)范围内的概率是________.
四、解答题
17.在标准化考试中既有单选题又有多选题,多选题是从A, B, C, D四个选项中选出所有正确的答案(四个选项中至少有两个选项是正确的).同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?
18.某手机厂家生产、、三种型号的手机,每种型号手机又分为标准版和版两个版本,某月的产量(单位:部)如表:
型号 型号 型号
标准版 200 650
版 300 350 600
该厂质检部门采用分层随机抽样的方法从这个月生产的手机中抽取100部,其中型号手机20部.
(1)求的值;
(2)在型号手机中采用分层随机抽样的方法抽取5部手机,再从这5部手机中任意抽取2部,求至多有1部手机为版的概率;
(3)该手机厂家所在城市的质量技术监督部门从型号手机中采用简单随机抽样的方法抽取了8部手机,经相关技术部门进行检测,这8部手机的综合质量得分分别为9.2、8.8、8.5、9.0、9.3、9.2、8.6、9.4(满分均为10分),将这8部手机的得分看成一个整体,若这8部手机中,与该整体平均得分之差的绝对值不超过0.3的概率低于0.65时,则该型号的手机不能投入市场.请通过计算判断型号手机是否能投入市场?
19.甲、乙两个乒乓球选手进行比赛,他们每一局获胜的概率均为,且每局比赛互补影响,规定“七局四胜”,即先赢四局者胜,若已知甲先赢了前两局,求:
(1)乙取胜的概率;
(2)设比赛局数为,求的分布列.
20.某单位一办公室现安排4个人去参加植树活动,该活动有甲、乙两个地点可供选择.约定:每个人通过掷一枚质地均匀的骰子决定自己去哪个地点植树,掷出点数为1或2的人去甲地,掷出点数大于2的人去乙地.
(1)求这4个人中恰有2人去甲地的概率;
(2)求这4个人中去甲地的人数大于去乙地的人数的概率;
(3)用X,Y分别表示这4个人中去甲、乙两地的人数,记,求随机变量的分布列与数学期望.
21.设某工厂有两个车间生产同型号家用电器,第一车间的次品率为0.15,第二车间的次品率为0.12,两个车间的成品都混合堆放在一个仓库.假设第一车间和第二车间生产的成品比例为2:3,今有一客户从成品仓库中随机提一台产品,求该产品合格的概率.
22.“水是生命之源”,但是据科学界统计,可用淡水资源仅占地球储水总量的2.8%,全世界近80%人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(单位:t):一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过随机抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照,,,分成9组,制成了如图所示的频率分布直方图.
(1)设该市有60万居民,估计全市居民中月均用水量不低于2.5 t的人数,并说明理由;
(2)若该市政府希望使82%的居民每月的用水不按议价收费,估计x的值,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
利用对立事件概率计算及条件概率公式推导出即可得解.
【详解】
依题意,,则,即,
于是得,所以事件与事件独立.
故选:C
2.B
【解析】
【分析】
由于车辆在任何时刻出现的概率都是独立的,所以观察到与观察不到的概率相等,又分钟小于分钟,根据题意,即可求出结果.
【详解】
由题意可知,在分钟内出现车辆的概率仅为,30分钟内不出现车辆的概率为0.2,30分钟内不出现车辆即是连续三个10分钟不出现车辆,即约等于0.6,
所以观察分钟就能发现车辆的概率约为.
故选:B.
3.B
【解析】
【分析】
设编号为随机变量,结合题设可得其各可能值的对应概率,再应用互斥事件概率的加法公式求即可.
【详解】
设任取1盆的编号为随机变量,
∴的可能取值为0,1,2,……,9,且,
∴.
故选:B.
4.D
【解析】
【分析】
根据互斥事件概率的加法关系即可求解.
【详解】
由题:A,B是互斥事件,
所以,
且,,
则.
故选:D
5.C
【解析】
【分析】
根据题意求得基本事件的总数,再利用列举法求得所求事件包含的基本事件的个数,利用古典摡型的概率计算公式,即可求解.
【详解】
设两款优惠套餐分别为A,B,甲乙丙三位同学,每人都有两种选法,
由分步计数原理,可得甲乙丙三位同学共有种不同的选法,
其中甲、乙、丙三位同学选择同一款套餐包括:有2种选法,
根据古典摡型的概率计算公式,可得概率为.
故选:C.
6.A
【解析】
【分析】
运用列举法得,今后的3天中恰有2天发布高温橙色预警信号的随机数有12个,由古典概型公式可得选项.
【详解】
解:今后的3天中恰有2天发布高温橙色预警信号的随机数有12个,分别为:
116, 812, 730, 452, 125, 217, 109, 361, 284, 147, 318, 027,
则今后的3天中恰有2天发布高温橙色预警信号的概率估计是:,
故选:A.
7.D
【解析】
【分析】
因为组合是与顺序无关的,所以A,B,C都是组合问题,D是排列问题.
【详解】
选项A中 ,是组合问题;选项B中,是组合问题;选项C中,是组合问题;选项D中 有顺序,是排列问题.
故选:D.
8.C
【解析】
【分析】
根据约束条件画出可行域,得到面积,根据几何概型得到答案.
【详解】
∵而满足构成钝角三角形,则需画出图像:
弓形面积:,∴.
故选
【点睛】
本题考查了几何概型,画出图像是解题的关键,意在考查学生的综合应用能力.
9.ABD
【解析】
【分析】
根据互斥事件的定义可判断各选项的正误,从而可得正确的选项.
【详解】
对于A,摸出三个白球事件和摸出三个黑球事件不可能同时发生,故它们为互斥事件,故A正确.
对于B,恰好有一黑球事件和都是黑球事件不可能同时发生,故它们为互斥事件,故B正确.
对于C,比如三个球中两个黑球和1个白球,则至少一个黑球事件和至多一个白球事件可同时发生,故C错误.
对于D,至少一个黑球事件和全是白球事件也不可能同时发生,故D正确.
故选:ABD.
10.BCD
【解析】
【分析】
由对立事件、互斥事件、并事件的概率计算公式代入计算,对选项逐一判断.
【详解】
“甲获胜”是“和棋或乙获胜”的对立事件,所以“甲获胜”的概率是,故A正确;设甲不输为事件A,则事件A是“甲获胜”和“和棋”这两个互斥事件的并事件,所以,故B错误;“乙输”的概率即“甲获胜”的概率,为,故C错误;设乙不输为事件B,则事件B是“乙获胜”和“和棋”这两个互斥事件的并事件,所以,故D错误;
故选:BCD
11.BD
【解析】
【分析】
根据互斥事件和对立事件的定义进行判断即可.
【详解】
由于,,,彼此互斥,且是必然事件,故事件的关系如图所示.
由图可知,任何一个事件与其余三个事件的并事件互为对立事件,任何两个事件的并事件与其余两个事件中任何一个是互斥事件,但不是对立事件,任何两个事件的并事件与其余两个事件的并事件互为对立事件,
故选:BD
12.ABD
【解析】
【分析】
计算得出,由此可得出结论.
【详解】
由题意可得,因为,,所以,,
故事件与相互独立.
故选:ABD.
13.
【解析】
【分析】
求出小明与第一代、第二代、第三代传播者接触的概率,利用独立事件、互斥事件的概率公式求解即可.
【详解】
设事件,,为第一代、第二代、第三代传播者接触,
事件为小明被感染,由已知得:
(A),(B),(C),,,,
(D)(A)(B)(C)
.
小明参加聚会,仅和感染的10个人其中一个接触,感染的概率为0.83.
故答案为:0.83.
【点睛】
本题考查概率的求法,考查独立事件、互斥事件的概率公式以及条件概率的性质等基础知识,考查运算求解能力,是基础题.
14.
【解析】
【分析】
求出所有事件的总数,求出三个砝码的总质量为9克的事件总数,然后用古典概率公式求解概率即可.
【详解】
编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,
从中随机选取三个,所有的事件总数为:,
这三个砝码的总质量为9克的事件只有:5,3,1或5,2,2两种情况,
所以:这三个砝码的总质量为9克的概率是:,
故答案为:.
15.30
【解析】
【分析】
由题可得共有种不同选法,然后计算3人都是男生或都是女生的选法,即求.
【详解】
从3名男生和4名女生中选3人参加志愿者活动,共有种不同选法,
其中3人都是男生或都是女生的选法有种,
所以选到的志愿者中既有男生又有女生的不同选法共有种.
故答案为:30.
16.0.02
【解析】
【分析】
把质量小于4.85 g的事件分拆成质量小于4.8 g的事件与质量在[4.8,4.85)(g)范围内的事件的和,再利用概率的加法公式即可得解.
【详解】
从羽毛球产品中任取一个,A={质量小于4.8 g},B={质量在[4.8,4.85)(g)范围内},C={质量小于4.85 g},
事件A与B互斥,且C=A+B,而P(A)=0.3,P(C)=0.32,
由P(C)=P(A+B)=P(A)+P(B),得P(B)=P(C)-P(A)=0.32-0.3=0.02,
所以质量在[4.8,4.85)(g)范围内的概率是0.02.
故答案为:0.02
17.答案见解析
【解析】
【分析】
列出基本事件个数,利用古典概型的概率计算公式求出概率即可得出答案.
【详解】
易知单选题猜对的概率为,对于多选题,
试验的样本空间为
{AB, AC, AD, BC, BD, CD, ABC, ABD, ACD, BCD, ABCD},
样本点共有11个,而正确答案只有1个,因此猜对的概率为 ,
因为<,即多选题猜对的概率小,所以多选题更难猜对.
18.(1)400
(2)
(3)该型号的手机不能投入市场
【解析】
【分析】
(1)根据分成抽样的知识,利用比例列方程,化简求得.
(2)结合古典概型概率计算公式,计算出所求概率.
(3)先求得总体平均分,然后求得“这8部手机中,与该整体平均得分之差的绝对值不超过0.3的概率”,进而作出判断.
(1)
由分层抽样的性质得:
,
解得.
(2)
在型号手机中采用分层随机抽样的方法抽取5部手机,
则标准版抽取部,版抽取部,
再从这5部手机中任意抽取2部,
基本事件总数,
至多有1部手机为版包含的基本事件个数,
至多有1部手机为版的概率.
(3)
这8部手机的综合质量得分分别为9.2、8.8、8.5、9.0、9.3、9.2、8.6、9.4(满分均为10分),
将这8部手机的得分看成一个整体,
该整体平均得分为,
这8部手机中,与该整体平均得分之差的绝对值不超过0.3的综合质量得分有:
9.2、8.8、9.0、9.3、9.2,共5个,
这8部手机中,与该整体平均得分之差的绝对值不超过0.3的概率,
该型号的手机不能投入市场.
19.(1)
(2)分布列见解析
【解析】
【分析】
(1)当甲先胜了前两局时,乙取胜的性质有两种:第一种是乙连胜三局,第二种是在第三局到第六局,乙胜了三局,第七局乙胜,求出两种情况的概率和可得答案;
(2)求出的可能取值和对应的概率可得答案.
(1)
当甲先胜了前两局时,乙取胜的性质有两种:第一种是乙连胜三局,第二种是在第三局到第六局,乙胜了三局,第七局乙胜,
第一种情况下乙取胜的概率为:,
第二种情况下乙取值的概率为:,
甲先赢了前两局,乙取胜的概率为
.
(2)
由已知得的可能取值为4,5,6,7,
,
,
,
,
的分布列为:
4 5 6 7
20.(1)
(2)
(3)分布列见解析,
【解析】
【分析】
(1)利用独立事件乘法公式求4个人中恰有2人去甲地的概率;
(2)由(1)知:4个人中恰有3或4人去甲地,应用互斥事件的加法公式,概率即可;
(3)根据(1)确定的可能值,并求出对应的概率,进而写出分布列,根据分布列求期望即可.
(1)
依题意知,这4个人中每个人去甲地的概率为,去乙地的概率为.
设“这4个人中恰有i人去甲地”为事件,则.
∴这4个人中恰有2人去甲地的概率.
(2)
设“这4个人中去甲地的人数大于去乙地的人数”为事件B,则.
由于与互斥,故.
∴这4个人中去甲地的人数大于去乙地的人数的概率为.
(3)
的所有可能的取值为0,2,4,由于与互斥,与互斥,
故,,.
∴的分布列为
0 2 4
P
故.
21.0.868
【解析】
【分析】
利用相互独立事件概率乘法公式能求出该产品合格的概率.
【详解】
设某工厂有两个车间生产同型号家用电器,第一车间的次品率为0.15,第二车间的次品率为0.12,
两个车间的成品都混合堆放在一个仓库,假设第1,2车间生产的成品比例为,
今有一客户从成品仓库中随机提一台产品,
则该产品合格的概率为.
该产品合格的概率为0.868.
22.(1)估计全市居民中月均用水量不低于2.5 t的人数为(万),理由见解析
(2)估计x的值为2.8,理由见解析
【解析】
【分析】
(1)先根据频率分布直方图求出月均用水量不低于2.5 t人数所占百分比,再乘以全市居民人数即可;
(2)先通过88%的居民月均用水量小于3 t得到,再根据计算即可.
(1)
由题图可知,不低于2.5 t人数所占百分比为,
所以估计全市居民中月均用水量不低于2.5 t的人数为(万).
(2)
由(1)可知,月均用水量小于2.5 t的居民人数所占百分比为73%,
即73%的居民月均用水量小于2.5 t,
则73%+
所以88%的居民月均用水量小于3 t,故,
所以.
故估计x的值为2.8.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
