第六章 圆周运动 单元测试(Word版含答案)
文档属性
| 名称 | 第六章 圆周运动 单元测试(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-14 16:33:01 | ||
图片预览



文档简介
圆周运动 单元测试
一、单项选择题(本题共13小题,每小题3分,共39分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列说法正确的是( )
A.匀速圆周运动是匀变速曲线运动
B.物体做离心运动是因为受到所谓离心力的作用
C.做匀速圆周运动的物体所受的合外力大小不变
D.匀速圆周运动的加速度恒定
2.某同学在课外活动时设计了一个小游戏,将质量为的滑块套在竖直杆上,滑块外侧有一轨道(可使轻绳绕滑块无摩擦转动),长为的轻绳一端与轨道相连,另一端与质量为的小球相连,滑块与竖直杆间的动摩擦因数。让小球绕竖直杆在水平面内做匀速圆周运动,重力加速度为。设最大静摩擦力等于滑动摩擦力,滑块恰不下滑,则小球做圆周运动的角速度为( )
A. B.
C. D.
3.如图甲所示,两个质量分别为m、2m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为2l,b与转轴的距离为l.如图乙所示(俯视图),两个质量均为m的小木块c和d(可视为质点)放在水平圆盘上,c与转轴、d与转轴的距离均为l,c与d之间用长度也为l的水平轻质细线相连。木块与圆盘之间的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴做角速度缓慢增大的转动,下列说法正确的是( )
A.图甲中,a、b同时开始滑动
B.图甲中,a所受的静摩擦力大于b所受的静摩擦力
C.图乙中,c、d与圆盘相对静止时,细线的最大拉力为kmg
D.图乙中,c、d与圆盘相对静止时,圆盘的最大角速度为
4.小明拿着一个正方体的光滑盒子在竖直平面内做半径为R的匀速圆周运动,盒子中有一个质量为m的小球(盒子的边长略大于球的直径),如图所示,在最高点时小球对盒子有向上大小为的压力,已知重力加速度为g,空气阻力不计,则( )
A.因为小球做匀速圆周运动,所以向心力恒定
B.该盒子做匀速圆周运动的周期等于
C.盒子运动到最低点时,对小球的作用力大小等于
D.盒子运动到O点等高的右侧位置时,小球受到的合力等于
5.质量为m的小球由轻绳a和b分别系于一轻质细杆的B点和A点,如图所示,绳a与水平方向成θ角,绳b在水平方向且长为l。当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是( )
A.a绳的张力可能为零
B.a绳的张力随角速度的增大而增大
C.当角速度,b绳将出现弹力
D.若b绳突然被剪断,则a绳的弹力一定发生变化
6.上海磁浮线路的最大转弯处半径达到8 000 m,近距离用肉眼看几乎是一条直线,而转弯处最小半径也达到1 300 m。一个质量为50 kg的乘客坐在以360 km/h的不变速率行驶的车里,随车驶过半径为2 500 m的弯道,下列说法正确的是( )
A.乘客受到的向心力大小约为100 N
B.乘客受到的向心力大小约为539 N
C.乘客受到的向心力大小约为300 N
D.乘客受到的向心力大小约为200 N
7.如图是汕尾市城区某环岛交通设施,路面水平,通过路口的车辆都按照逆时针方向行进。假设某时甲、乙两车匀速通过环形路段,甲行驶在内侧,乙行驶在外侧,它们转弯时线速度大小相等,设甲所在车道的轨道半径为,乙所在车道的轨道半径为。假设汽车受到的最大静摩擦力等于车重的0.8倍,g取,则关于此过程中两汽车的运动,下列说法正确的是( )
乙车的最大速度可以达到
B.当乙车的速度大于时,可能会撞上甲车
C.两车的角速度大小相等
D.向心加速度大小:
8.滚筒洗衣机静止于水平地面上,衣物随着滚筒一起在竖直平面内做高速匀速圆周运动,以达到脱水的效果。滚筒截面如图所示,下列说法正确的是( )
A.衣物运动的过程中洗衣机对地面的压力不变
B.衣物运动到最低点B点时处于失重状态
C.衣物运动的过程中洗衣机对地而的摩擦力始终为0
D.衣物运动到最低点B点时受到滚筒的作用力最大,脱水效果更好
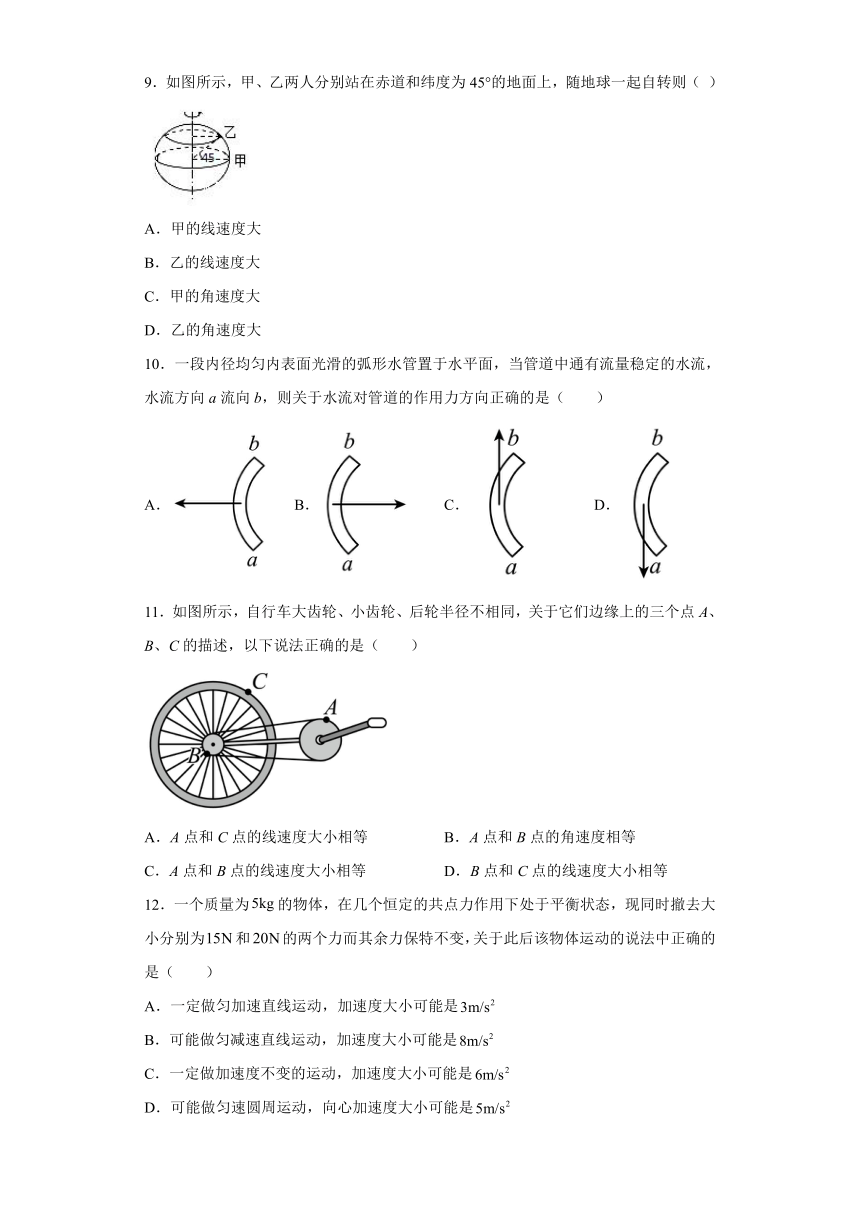
9.如图所示,甲、乙两人分别站在赤道和纬度为45°的地面上,随地球一起自转则( )
A.甲的线速度大
B.乙的线速度大
C.甲的角速度大
D.乙的角速度大
10.一段内径均匀内表面光滑的弧形水管置于水平面,当管道中通有流量稳定的水流,水流方向a流向b,则关于水流对管道的作用力方向正确的是( )
A. B. C. D.
11.如图所示,自行车大齿轮、小齿轮、后轮半径不相同,关于它们边缘上的三个点A、B、C的描述,以下说法正确的是( )
A.A点和C点的线速度大小相等 B.A点和B点的角速度相等
C.A点和B点的线速度大小相等 D.B点和C点的线速度大小相等
12.一个质量为的物体,在几个恒定的共点力作用下处于平衡状态,现同时撤去大小分别为和的两个力而其余力保特不变,关于此后该物体运动的说法中正确的是( )
A.一定做匀加速直线运动,加速度大小可能是
B.可能做匀减速直线运动,加速度大小可能是
C.一定做加速度不变的运动,加速度大小可能是
D.可能做匀速圆周运动,向心加速度大小可能是
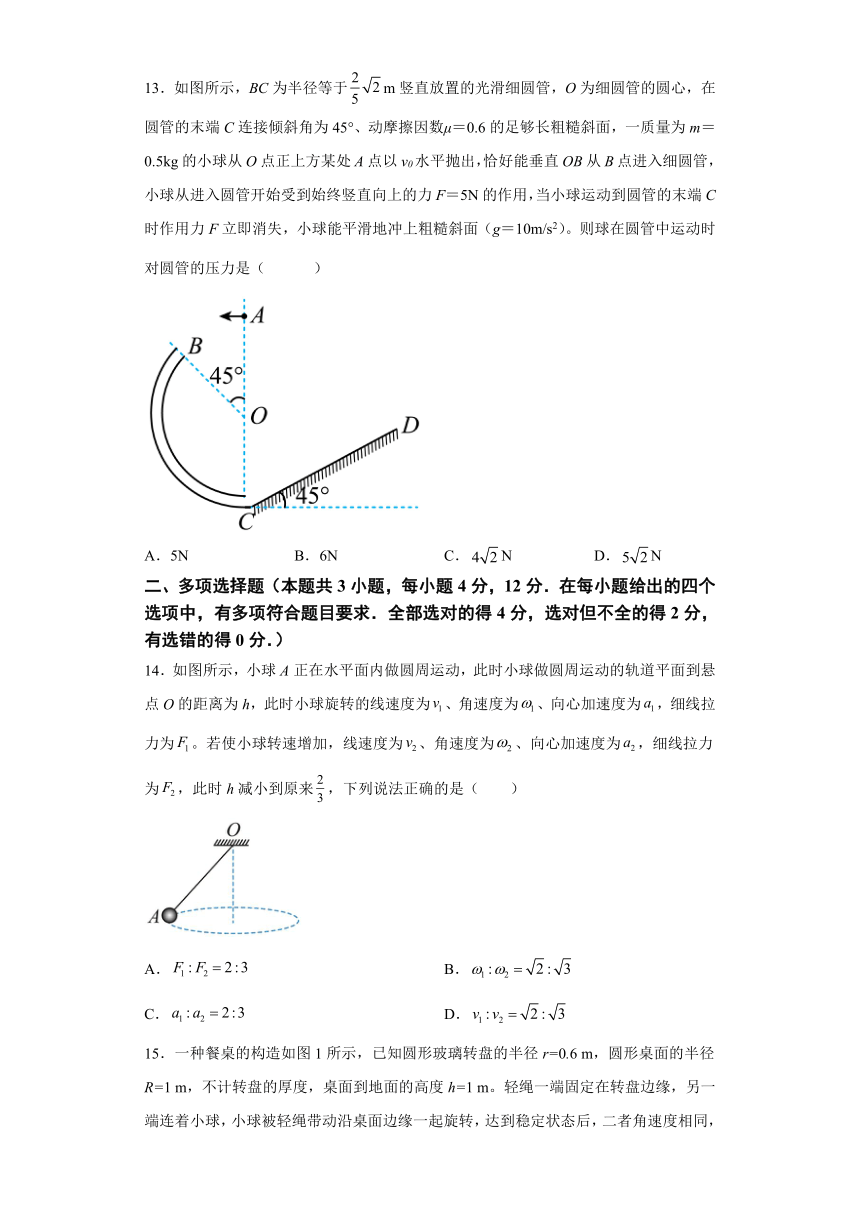
13.如图所示,BC为半径等于m竖直放置的光滑细圆管,O为细圆管的圆心,在圆管的末端C连接倾斜角为45°、动摩擦因数μ=0.6的足够长粗糙斜面,一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始受到始终竖直向上的力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失,小球能平滑地冲上粗糙斜面(g=10m/s2)。则球在圆管中运动时对圆管的压力是( )
A.5N B.6N C.N D.N
二、多项选择题(本题共3小题,每小题4分,12分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得4分,选对但不全的得2分,有选错的得0分.)
14.如图所示,小球A正在水平面内做圆周运动,此时小球做圆周运动的轨道平面到悬点O的距离为h,此时小球旋转的线速度为、角速度为、向心加速度为,细线拉力为。若使小球转速增加,线速度为、角速度为、向心加速度为,细线拉力为,此时h减小到原来,下列说法正确的是( )
A. B.
C. D.
15.一种餐桌的构造如图1所示,已知圆形玻璃转盘的半径r=0.6 m,圆形桌面的半径R=1 m,不计转盘的厚度,桌面到地面的高度h=1 m。轻绳一端固定在转盘边缘,另一端连着小球,小球被轻绳带动沿桌面边缘一起旋转,达到稳定状态后,二者角速度相同,俯视图如图2所示。某时刻绳子突然断裂,小球沿桌面边缘飞出后的落地点到桌面和转盘共同圆心的距离s= m,重力加速度g取10 m/s2。则( )
A.小球飞出桌面边缘的速度大小为 m/s
B.小球飞出桌面边缘的速度大小为 m/s
C.小球与桌面之间的动摩擦因数为0.75
D.小球与桌面之间的动摩擦因数为0.375
16.汕头海湾隧道工程采取的是隧道盾构挖掘技术。盾构机刀盘直径为15.01米,相当于五层楼高。其基本工作原理是:沿隧洞轴线向前推进,同时通过旋转前端盾形结构,利用安装在前端的刀盘对土壤进行开挖切削,挖掘出来的土碴被输送到后方。如图所示为某盾构机前端,以下说法中正确的是( )
A.盾构机前端转动时,各个刀片转动的角速度相同
B.盾构机前端转动时,各个刀片的线速度随半径的增大而减小
C.当盾构机前端转速为3r/min时,其转动周期为0.05s
D.当盾构机前端转速为3r/min时,前端外边缘的线速度约为2.4m/s
三、填空题(每空2分,共14分)
17.某物体做匀速圆周运动,圆周的半径为R,周期为T,物体在运动的时间内,位移的大小是_____,路程是_________,转过的角度是_________。
18.一位同学习了圆周运动的知识后,要对变速自行车的变速原理进行研究,假设某种变速自行车有六个飞轮和三个链轮。
名称 链轮 飞轮
齿数N/个 48 38 28 15 16 18 21 24 28
(1)如图所示前、后轮直径约为660mm,链轮和飞轮的齿数如表所示,人骑该车行进速度为4m/s时,前轮的角速度为______rad/s;脚踩踏板做匀速圆周运动的角速度最小值约为________rad/s。(结果保留两位小数)
(2)把链轮半径和飞轮半径的比值k=r2/r3称为变速比,如果踏板的角速度为ω,车轮的半径为R,则变速自行车的速度为_______(用字母表示),由此可见,在脚踩踏板的角速度一定时,要提高车速,就要________。
四、解答题
19.(10分)会展用旋转展示台展示物品。简化如图所示,水平圆盘形展台半径为R = 0.65m,圆盘平面距水平地面的高度为h = 1.2m,绕竖直中心轴OO′在水平面做匀速圆周运动,某展品(可视为质点)放在展示圆盘上距轴心r = 0.6m的位置在静摩擦力作用下随圆盘一起运动,展品与展台间的动摩擦因数为μ = 0.54,最大静摩擦力等于滑动摩擦力,忽略空气阻力,取重力加速度g = 10m/s2。
(1)求圆盘展台匀速转动时允许的最大角速度大小;
(2)当圆盘展台以最大角速度转动时,展台因故突然停止转动,判断物品是否能从圆盘展台上滑落下来,如果不能滑落请通过计算说明理由;如果能,请计算出物品落地点到转轴的水平距离。
20.(12分)如图是场地自行车比赛的圆形赛道。圆周的半径为40m,路面与水平面的夹角为37°,(sin37°=0.6,cos37°=0.8),不考虑空气阻力,g=10m/s2。
(1)某运动员骑自行车在该赛道上做匀速圆周运动,要使自行车不受摩擦力作用,其速度应等于多少?
(2)若该运动员骑自行车以20m/s的速度仍沿该赛道做匀速圆周运动,自行车和运动员的质量一共是80kg,此时自行车所受摩擦力的大小又是多少?方向如何?
21.(13分)“太极球”是近年来在广大市民中较流行的一种健身器材。做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上。现将球拍和太极球简化成如图甲所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势。A为圆周的最高点,C为最低点,B、D与圆心O等高。设球的重力为1N,不计拍的重力。则∶
(1)健身者在C处所需施加的力比在A处大多少?
(2)设在A处时健身者需施加的力为F,当球运动到B、D位置时,板与水平方向需有一定的夹角θ,请作出tanθ-F的关系图像。
试卷第1页,共3页
参考答案:
1.C
【解析】
【详解】
AD.匀速圆周运动的加速度方向改变,则加速度改变,不是匀变速曲线运动,故AD错误;
B.物体做离心运动是因为所受合力小于做圆周运动需要的向心力,故B错误;
C.做匀速圆周运动的物体所受的合外力大小不变,方向改变,故C正确。
故选C。
2.A
【解析】
【分析】
本题考查圆周运动规律、摩擦力和牛顿第二定律等知识,考查考生的理解能力和分析综合能力。
【详解】
设轻绳与竖直方向夹角为,小球做匀速圆周运动,有
、一定,有
解得
故A正确,BCD错误。
故选A。
3.D
【解析】
【详解】
A.在题图甲中
r越大,开始滑动时的角速度越小,则a先滑动,A错误;
B.对木块a有
对b有
即a、b所受的静摩擦力始终相等,B错误;
CD.在题图乙中,当时,细线的拉力和最大静摩擦力提供木块做匀速圆周运动的向心力,当最大静摩擦力的方向与细线垂直时,如图所示
木块受到的合力F最大,圆盘转动的角速度最大
解得
此时
C错误D正确。
故选D。
4.C
【解析】
【详解】
A.小球做匀速圆周运动,合外力作为向心力,大小恒定,方向始终指向圆心,故向心力是变力,A错误;
B.由题意可知,在最高点时盒子对小球有向下的压力,大小为,由向心力公式可得
解得盒子运动的周期为
B错误;
C.在最低点时,对小球由向心力公式可得
又
联立解得盒子对小球的作用力大小为
C正确;
D.盒子运动到O点等高的右侧位置时,小球受到的合力等于向心力,大小为,D错误。
故选C。
5.C
【解析】
【详解】
A.由于小球m的重力不为零,a绳的张力不可能为零,b绳的张力可能为零,故A错误;
B.由于a绳的张力在竖直方向的分力等于重力,角θ不变,所以a绳张力不变,b绳的张力随角速度的增大而增大,故B错误;
C.若b绳中的张力为零,设a绳中的张力为F,对小球m
Fsin θ=mg,Fcosθ=mω2l
解得
即当角速度
b绳将出现弹力,故C正确;
D.若,b绳突然被剪断时,a绳的弹力不发生变化,故D错误。
故选C。
6.D
【解析】
【详解】
360km/h=100m/s,乘客所受的向心力
故选D。
7.D
【解析】
【详解】
A.乙汽车转弯的半径为,乙车受到的最大静摩擦力提供向心力,则有
解得
故A错误;
B.当乙车速度大于时,乙车会做离心运动,往弯道外侧移动,不会撞上甲车。故B错误;
C.由于题中已知二者线速度大小相等
由于,根据可知二者角速度大小关系为
故C错误:
D.根据公式可知二者向心加速度大小关系为
故D正确。
故选D。
8.D
【解析】
【详解】
A.由于衣物在运动中,加速度方向总是指向洗衣机滚桶的圆心,由牛顿第二定律可知,衣物对洗衣机滚桶的作用力产生变化,对洗衣机受力分析,洗衣机静止不动,可推知洗衣机对地面的压力会产生变化,A错误;
B.衣物运动到最低点B点时,加速度方向竖直向上,处于超重状态,B错误;
C.在衣物运动中,当衣物处在滚桶的最高点或最低点时,衣物对洗衣机在水平方向没有作用力,洗衣机在水平方向没有运动的趋势,对地而的摩擦力是0,当衣物运动离开最高点或最低点时,衣物对洗衣机在水平方向有作用力,使洗衣机在水平方向有运动的趋势,对地面有摩擦力产生,C错误;
D.衣物运动到最低点B点时,加速度方向竖直向上,处于超重状态,由牛顿第二定律可知,衣物在B点受到滚筒的作用力最大,脱水效果更好,D正确。
故选D。
9.A
【解析】
【详解】
甲、乙两人随地球一起自转,角速度相等,CD错误;甲的转动半径大于乙的转动半径,由,甲的线速度大,A正确、B错误.
10.A
【解析】
【详解】
水在圆弧管道内做匀速圆周运动,根据圆周运动的条件可知,水受到的合外力提供向心力,所以水流受到的合外力的方向向右,结合牛顿第三定律可知水流对管道的作用力方向向左。
故选A。
11.C
【解析】
【详解】
ACD.大齿轮、小齿轮通过链条传动,A、B两点是大、小齿轮的边缘点,所以A、B两点的线速度大小相等;小齿轮和后轮同轴转动,B、C两点分别在小齿轮和后轮边缘,故角速度相等,根据
v=ωr
可知B点的线速度小于C点的线速度,所以A点的线速度小于C点的线速度,故A、D错误,C正确。
B.A、B两点的线速度大小相等,A的半径大于B的半径,根据
ω=
得B点的角速度大于A点的角速度,故B错误。
故选C。
12.C
【解析】
【详解】
物体原来受力平衡,撤去两个力之后,剩余力的合力与撤去的两力的合力等大反向,合力范围在5N~35N之间,根据牛顿第二定律
F=ma
其余力保特不变,所以加速度不变,物体一定是匀变速运动;加速度在1m/s2~7m/s2之间;因为不知道初速度方向,所以不能确定速度与合外力是否共线,不能确定物体作直线运动还是曲线运动,但一定是匀变速运动。
故选C。
13.D
【解析】
【详解】
小球从A运动到B做平抛运动,有
在B点有
联立得
v0=2m/s
在B点据平抛运动的速度规律可得,小球的速度大小为
小球从进入圆管开始受到始终竖直向上的力F=5N的作用,恰好与小球所受重力平衡,故小球从B到C以速度v做匀速圆周运动,据向心力公式可得,小球受到的支持力大小为
则球在圆管中运动时对圆管的压力大小为。
故选D。
14.AB
【解析】
【详解】
A.设悬线与竖直方向的夹角为,由
可得
A正确;
B.由
可得
可得
B正确;
C.向心加速度
向心加速度之比
由几何关系可得
由于
因此
C错误;
D.由
可得线速度之比
D错误。
故选AB。
15.AD
【解析】
【详解】
AB.小球沿桌面边缘飞出后做平抛运动,竖直方向有
水平方向有
由几何关系知,落地点到桌面和转盘共同圆心的距离
联立解得小球飞出桌面边缘的速度
B错误A正确;
CD.对小球进行受力分析,设绳子拉力大小为F,方向与过小球和圆心的直线的夹角为θ,则
小球受到的向心力由绳子的拉力、摩擦力共同提供,故
又
联立解得小球与桌面之间的动摩擦因数
C错误D正确。
故选AD。
16.AD
【解析】
【详解】
A.因为盾构机前端的各刀片同轴转动,所以各刀片的角速度相等,故A正确;
B.根据v=rω可知,角速度相等,各刀片的线速度随半径的增大而增大,故B错误;
C.因为转速
n=3r/min=0.05r/s
所以转动周期为
T=s=20s
故C错误;
D.根据v=2πrn知,盾构机前端外边缘的线速度大小为
v=2×3.14×7.505×0.05m/s≈2.4m/s
故D正确。
故选AD。
17.
【详解】
某物体做匀速圆周运动,圆周的半径为R,周期为T,在运动的时间内,位移的大小
路程
运动的角速度
转过的角度是
18. 12 3.75 增大链轮和车轮半径,减小飞轮的半径。
【详解】
(1)飞轮的角速度与后轮的角速度相等,根据v=ωr得:
后轮的角速度与前轮相等为定值,即飞轮的角速度一定。由于
R链ω链=R飞ω飞
链轮的角速度与脚踏板的角速度相同,要想脚踏板的角速度最小,则飞轮的半径最小,链轮的半径最大;根据v=ωr得
(2)依据同带的瞬时速率相等,则有
R链ω链=R飞ω飞
而飞轮的角速度与后轮的角速度相等,因此车轮的速度
由此可见,在脚踩踏板的角速度一定时,要提高车速,就要增大链轮和车轮半径,减小飞轮的半径。
19.(1)3rad/s;(2)会滑落,0.86m
【详解】
(1)最大静摩擦力提供向心力有
μmg = mω2r
解得
ω = 3rad/s
(2)圆盘停下时,展品速度
vmax = ωr = 1.8m/s
展品在圆盘上做匀减速直线运动最大位移为
x = = 0.25m
展品在圆盘上做匀减速直线运动加速度满足
μmg = ma
物块运动到圆盘边沿时的速度v1满足
vmax2 - v12 = 2ax
解得
v1 = m/s > 0
可知展品会滑落
平抛运动时,竖直方向有
h = gt2
水平方向,落点距离抛点的水平距离
x1 = v1t = 0.36m
如图所示,则落点都转轴的水平距离为
L = = 0.86m
20.(1);(2)160N,方向沿路面向下
【详解】
(1)运动员受力如图
根据牛顿第二定律,可得
代入数据,解得
运动员所需向心力F=mgtan θ=450N
(2)当自行车速为,此时重力和支持力的合力不足以提供向心力,斜面对人和自行车施加沿斜面向下的静摩擦力,其受力分析如图所示
根据牛顿第二定律可得,在竖直方向有
在水平方向有
联立解得
21.(1)2N; (2)
【详解】
(1)由于小球在A处的速度大小为v,半径为R
则在A处时有
①
可得
在C处时,有
②
由①②式得
△F=F′-F=2mg=2 N
(2)在A处时板对小球的作用力为F,球做匀速圆周运动的向心力
F向=F+mg
由于无相对运动趋势,在B处不受摩擦力作用,受力分析如图所示。
则
作出的tan θ-F的关系图像如图所示
答案第1页,共2页
答案第1页,共2页
一、单项选择题(本题共13小题,每小题3分,共39分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列说法正确的是( )
A.匀速圆周运动是匀变速曲线运动
B.物体做离心运动是因为受到所谓离心力的作用
C.做匀速圆周运动的物体所受的合外力大小不变
D.匀速圆周运动的加速度恒定
2.某同学在课外活动时设计了一个小游戏,将质量为的滑块套在竖直杆上,滑块外侧有一轨道(可使轻绳绕滑块无摩擦转动),长为的轻绳一端与轨道相连,另一端与质量为的小球相连,滑块与竖直杆间的动摩擦因数。让小球绕竖直杆在水平面内做匀速圆周运动,重力加速度为。设最大静摩擦力等于滑动摩擦力,滑块恰不下滑,则小球做圆周运动的角速度为( )
A. B.
C. D.
3.如图甲所示,两个质量分别为m、2m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为2l,b与转轴的距离为l.如图乙所示(俯视图),两个质量均为m的小木块c和d(可视为质点)放在水平圆盘上,c与转轴、d与转轴的距离均为l,c与d之间用长度也为l的水平轻质细线相连。木块与圆盘之间的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴做角速度缓慢增大的转动,下列说法正确的是( )
A.图甲中,a、b同时开始滑动
B.图甲中,a所受的静摩擦力大于b所受的静摩擦力
C.图乙中,c、d与圆盘相对静止时,细线的最大拉力为kmg
D.图乙中,c、d与圆盘相对静止时,圆盘的最大角速度为
4.小明拿着一个正方体的光滑盒子在竖直平面内做半径为R的匀速圆周运动,盒子中有一个质量为m的小球(盒子的边长略大于球的直径),如图所示,在最高点时小球对盒子有向上大小为的压力,已知重力加速度为g,空气阻力不计,则( )
A.因为小球做匀速圆周运动,所以向心力恒定
B.该盒子做匀速圆周运动的周期等于
C.盒子运动到最低点时,对小球的作用力大小等于
D.盒子运动到O点等高的右侧位置时,小球受到的合力等于
5.质量为m的小球由轻绳a和b分别系于一轻质细杆的B点和A点,如图所示,绳a与水平方向成θ角,绳b在水平方向且长为l。当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是( )
A.a绳的张力可能为零
B.a绳的张力随角速度的增大而增大
C.当角速度,b绳将出现弹力
D.若b绳突然被剪断,则a绳的弹力一定发生变化
6.上海磁浮线路的最大转弯处半径达到8 000 m,近距离用肉眼看几乎是一条直线,而转弯处最小半径也达到1 300 m。一个质量为50 kg的乘客坐在以360 km/h的不变速率行驶的车里,随车驶过半径为2 500 m的弯道,下列说法正确的是( )
A.乘客受到的向心力大小约为100 N
B.乘客受到的向心力大小约为539 N
C.乘客受到的向心力大小约为300 N
D.乘客受到的向心力大小约为200 N
7.如图是汕尾市城区某环岛交通设施,路面水平,通过路口的车辆都按照逆时针方向行进。假设某时甲、乙两车匀速通过环形路段,甲行驶在内侧,乙行驶在外侧,它们转弯时线速度大小相等,设甲所在车道的轨道半径为,乙所在车道的轨道半径为。假设汽车受到的最大静摩擦力等于车重的0.8倍,g取,则关于此过程中两汽车的运动,下列说法正确的是( )
乙车的最大速度可以达到
B.当乙车的速度大于时,可能会撞上甲车
C.两车的角速度大小相等
D.向心加速度大小:
8.滚筒洗衣机静止于水平地面上,衣物随着滚筒一起在竖直平面内做高速匀速圆周运动,以达到脱水的效果。滚筒截面如图所示,下列说法正确的是( )
A.衣物运动的过程中洗衣机对地面的压力不变
B.衣物运动到最低点B点时处于失重状态
C.衣物运动的过程中洗衣机对地而的摩擦力始终为0
D.衣物运动到最低点B点时受到滚筒的作用力最大,脱水效果更好
9.如图所示,甲、乙两人分别站在赤道和纬度为45°的地面上,随地球一起自转则( )
A.甲的线速度大
B.乙的线速度大
C.甲的角速度大
D.乙的角速度大
10.一段内径均匀内表面光滑的弧形水管置于水平面,当管道中通有流量稳定的水流,水流方向a流向b,则关于水流对管道的作用力方向正确的是( )
A. B. C. D.
11.如图所示,自行车大齿轮、小齿轮、后轮半径不相同,关于它们边缘上的三个点A、B、C的描述,以下说法正确的是( )
A.A点和C点的线速度大小相等 B.A点和B点的角速度相等
C.A点和B点的线速度大小相等 D.B点和C点的线速度大小相等
12.一个质量为的物体,在几个恒定的共点力作用下处于平衡状态,现同时撤去大小分别为和的两个力而其余力保特不变,关于此后该物体运动的说法中正确的是( )
A.一定做匀加速直线运动,加速度大小可能是
B.可能做匀减速直线运动,加速度大小可能是
C.一定做加速度不变的运动,加速度大小可能是
D.可能做匀速圆周运动,向心加速度大小可能是
13.如图所示,BC为半径等于m竖直放置的光滑细圆管,O为细圆管的圆心,在圆管的末端C连接倾斜角为45°、动摩擦因数μ=0.6的足够长粗糙斜面,一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始受到始终竖直向上的力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失,小球能平滑地冲上粗糙斜面(g=10m/s2)。则球在圆管中运动时对圆管的压力是( )
A.5N B.6N C.N D.N
二、多项选择题(本题共3小题,每小题4分,12分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得4分,选对但不全的得2分,有选错的得0分.)
14.如图所示,小球A正在水平面内做圆周运动,此时小球做圆周运动的轨道平面到悬点O的距离为h,此时小球旋转的线速度为、角速度为、向心加速度为,细线拉力为。若使小球转速增加,线速度为、角速度为、向心加速度为,细线拉力为,此时h减小到原来,下列说法正确的是( )
A. B.
C. D.
15.一种餐桌的构造如图1所示,已知圆形玻璃转盘的半径r=0.6 m,圆形桌面的半径R=1 m,不计转盘的厚度,桌面到地面的高度h=1 m。轻绳一端固定在转盘边缘,另一端连着小球,小球被轻绳带动沿桌面边缘一起旋转,达到稳定状态后,二者角速度相同,俯视图如图2所示。某时刻绳子突然断裂,小球沿桌面边缘飞出后的落地点到桌面和转盘共同圆心的距离s= m,重力加速度g取10 m/s2。则( )
A.小球飞出桌面边缘的速度大小为 m/s
B.小球飞出桌面边缘的速度大小为 m/s
C.小球与桌面之间的动摩擦因数为0.75
D.小球与桌面之间的动摩擦因数为0.375
16.汕头海湾隧道工程采取的是隧道盾构挖掘技术。盾构机刀盘直径为15.01米,相当于五层楼高。其基本工作原理是:沿隧洞轴线向前推进,同时通过旋转前端盾形结构,利用安装在前端的刀盘对土壤进行开挖切削,挖掘出来的土碴被输送到后方。如图所示为某盾构机前端,以下说法中正确的是( )
A.盾构机前端转动时,各个刀片转动的角速度相同
B.盾构机前端转动时,各个刀片的线速度随半径的增大而减小
C.当盾构机前端转速为3r/min时,其转动周期为0.05s
D.当盾构机前端转速为3r/min时,前端外边缘的线速度约为2.4m/s
三、填空题(每空2分,共14分)
17.某物体做匀速圆周运动,圆周的半径为R,周期为T,物体在运动的时间内,位移的大小是_____,路程是_________,转过的角度是_________。
18.一位同学习了圆周运动的知识后,要对变速自行车的变速原理进行研究,假设某种变速自行车有六个飞轮和三个链轮。
名称 链轮 飞轮
齿数N/个 48 38 28 15 16 18 21 24 28
(1)如图所示前、后轮直径约为660mm,链轮和飞轮的齿数如表所示,人骑该车行进速度为4m/s时,前轮的角速度为______rad/s;脚踩踏板做匀速圆周运动的角速度最小值约为________rad/s。(结果保留两位小数)
(2)把链轮半径和飞轮半径的比值k=r2/r3称为变速比,如果踏板的角速度为ω,车轮的半径为R,则变速自行车的速度为_______(用字母表示),由此可见,在脚踩踏板的角速度一定时,要提高车速,就要________。
四、解答题
19.(10分)会展用旋转展示台展示物品。简化如图所示,水平圆盘形展台半径为R = 0.65m,圆盘平面距水平地面的高度为h = 1.2m,绕竖直中心轴OO′在水平面做匀速圆周运动,某展品(可视为质点)放在展示圆盘上距轴心r = 0.6m的位置在静摩擦力作用下随圆盘一起运动,展品与展台间的动摩擦因数为μ = 0.54,最大静摩擦力等于滑动摩擦力,忽略空气阻力,取重力加速度g = 10m/s2。
(1)求圆盘展台匀速转动时允许的最大角速度大小;
(2)当圆盘展台以最大角速度转动时,展台因故突然停止转动,判断物品是否能从圆盘展台上滑落下来,如果不能滑落请通过计算说明理由;如果能,请计算出物品落地点到转轴的水平距离。
20.(12分)如图是场地自行车比赛的圆形赛道。圆周的半径为40m,路面与水平面的夹角为37°,(sin37°=0.6,cos37°=0.8),不考虑空气阻力,g=10m/s2。
(1)某运动员骑自行车在该赛道上做匀速圆周运动,要使自行车不受摩擦力作用,其速度应等于多少?
(2)若该运动员骑自行车以20m/s的速度仍沿该赛道做匀速圆周运动,自行车和运动员的质量一共是80kg,此时自行车所受摩擦力的大小又是多少?方向如何?
21.(13分)“太极球”是近年来在广大市民中较流行的一种健身器材。做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上。现将球拍和太极球简化成如图甲所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势。A为圆周的最高点,C为最低点,B、D与圆心O等高。设球的重力为1N,不计拍的重力。则∶
(1)健身者在C处所需施加的力比在A处大多少?
(2)设在A处时健身者需施加的力为F,当球运动到B、D位置时,板与水平方向需有一定的夹角θ,请作出tanθ-F的关系图像。
试卷第1页,共3页
参考答案:
1.C
【解析】
【详解】
AD.匀速圆周运动的加速度方向改变,则加速度改变,不是匀变速曲线运动,故AD错误;
B.物体做离心运动是因为所受合力小于做圆周运动需要的向心力,故B错误;
C.做匀速圆周运动的物体所受的合外力大小不变,方向改变,故C正确。
故选C。
2.A
【解析】
【分析】
本题考查圆周运动规律、摩擦力和牛顿第二定律等知识,考查考生的理解能力和分析综合能力。
【详解】
设轻绳与竖直方向夹角为,小球做匀速圆周运动,有
、一定,有
解得
故A正确,BCD错误。
故选A。
3.D
【解析】
【详解】
A.在题图甲中
r越大,开始滑动时的角速度越小,则a先滑动,A错误;
B.对木块a有
对b有
即a、b所受的静摩擦力始终相等,B错误;
CD.在题图乙中,当时,细线的拉力和最大静摩擦力提供木块做匀速圆周运动的向心力,当最大静摩擦力的方向与细线垂直时,如图所示
木块受到的合力F最大,圆盘转动的角速度最大
解得
此时
C错误D正确。
故选D。
4.C
【解析】
【详解】
A.小球做匀速圆周运动,合外力作为向心力,大小恒定,方向始终指向圆心,故向心力是变力,A错误;
B.由题意可知,在最高点时盒子对小球有向下的压力,大小为,由向心力公式可得
解得盒子运动的周期为
B错误;
C.在最低点时,对小球由向心力公式可得
又
联立解得盒子对小球的作用力大小为
C正确;
D.盒子运动到O点等高的右侧位置时,小球受到的合力等于向心力,大小为,D错误。
故选C。
5.C
【解析】
【详解】
A.由于小球m的重力不为零,a绳的张力不可能为零,b绳的张力可能为零,故A错误;
B.由于a绳的张力在竖直方向的分力等于重力,角θ不变,所以a绳张力不变,b绳的张力随角速度的增大而增大,故B错误;
C.若b绳中的张力为零,设a绳中的张力为F,对小球m
Fsin θ=mg,Fcosθ=mω2l
解得
即当角速度
b绳将出现弹力,故C正确;
D.若,b绳突然被剪断时,a绳的弹力不发生变化,故D错误。
故选C。
6.D
【解析】
【详解】
360km/h=100m/s,乘客所受的向心力
故选D。
7.D
【解析】
【详解】
A.乙汽车转弯的半径为,乙车受到的最大静摩擦力提供向心力,则有
解得
故A错误;
B.当乙车速度大于时,乙车会做离心运动,往弯道外侧移动,不会撞上甲车。故B错误;
C.由于题中已知二者线速度大小相等
由于,根据可知二者角速度大小关系为
故C错误:
D.根据公式可知二者向心加速度大小关系为
故D正确。
故选D。
8.D
【解析】
【详解】
A.由于衣物在运动中,加速度方向总是指向洗衣机滚桶的圆心,由牛顿第二定律可知,衣物对洗衣机滚桶的作用力产生变化,对洗衣机受力分析,洗衣机静止不动,可推知洗衣机对地面的压力会产生变化,A错误;
B.衣物运动到最低点B点时,加速度方向竖直向上,处于超重状态,B错误;
C.在衣物运动中,当衣物处在滚桶的最高点或最低点时,衣物对洗衣机在水平方向没有作用力,洗衣机在水平方向没有运动的趋势,对地而的摩擦力是0,当衣物运动离开最高点或最低点时,衣物对洗衣机在水平方向有作用力,使洗衣机在水平方向有运动的趋势,对地面有摩擦力产生,C错误;
D.衣物运动到最低点B点时,加速度方向竖直向上,处于超重状态,由牛顿第二定律可知,衣物在B点受到滚筒的作用力最大,脱水效果更好,D正确。
故选D。
9.A
【解析】
【详解】
甲、乙两人随地球一起自转,角速度相等,CD错误;甲的转动半径大于乙的转动半径,由,甲的线速度大,A正确、B错误.
10.A
【解析】
【详解】
水在圆弧管道内做匀速圆周运动,根据圆周运动的条件可知,水受到的合外力提供向心力,所以水流受到的合外力的方向向右,结合牛顿第三定律可知水流对管道的作用力方向向左。
故选A。
11.C
【解析】
【详解】
ACD.大齿轮、小齿轮通过链条传动,A、B两点是大、小齿轮的边缘点,所以A、B两点的线速度大小相等;小齿轮和后轮同轴转动,B、C两点分别在小齿轮和后轮边缘,故角速度相等,根据
v=ωr
可知B点的线速度小于C点的线速度,所以A点的线速度小于C点的线速度,故A、D错误,C正确。
B.A、B两点的线速度大小相等,A的半径大于B的半径,根据
ω=
得B点的角速度大于A点的角速度,故B错误。
故选C。
12.C
【解析】
【详解】
物体原来受力平衡,撤去两个力之后,剩余力的合力与撤去的两力的合力等大反向,合力范围在5N~35N之间,根据牛顿第二定律
F=ma
其余力保特不变,所以加速度不变,物体一定是匀变速运动;加速度在1m/s2~7m/s2之间;因为不知道初速度方向,所以不能确定速度与合外力是否共线,不能确定物体作直线运动还是曲线运动,但一定是匀变速运动。
故选C。
13.D
【解析】
【详解】
小球从A运动到B做平抛运动,有
在B点有
联立得
v0=2m/s
在B点据平抛运动的速度规律可得,小球的速度大小为
小球从进入圆管开始受到始终竖直向上的力F=5N的作用,恰好与小球所受重力平衡,故小球从B到C以速度v做匀速圆周运动,据向心力公式可得,小球受到的支持力大小为
则球在圆管中运动时对圆管的压力大小为。
故选D。
14.AB
【解析】
【详解】
A.设悬线与竖直方向的夹角为,由
可得
A正确;
B.由
可得
可得
B正确;
C.向心加速度
向心加速度之比
由几何关系可得
由于
因此
C错误;
D.由
可得线速度之比
D错误。
故选AB。
15.AD
【解析】
【详解】
AB.小球沿桌面边缘飞出后做平抛运动,竖直方向有
水平方向有
由几何关系知,落地点到桌面和转盘共同圆心的距离
联立解得小球飞出桌面边缘的速度
B错误A正确;
CD.对小球进行受力分析,设绳子拉力大小为F,方向与过小球和圆心的直线的夹角为θ,则
小球受到的向心力由绳子的拉力、摩擦力共同提供,故
又
联立解得小球与桌面之间的动摩擦因数
C错误D正确。
故选AD。
16.AD
【解析】
【详解】
A.因为盾构机前端的各刀片同轴转动,所以各刀片的角速度相等,故A正确;
B.根据v=rω可知,角速度相等,各刀片的线速度随半径的增大而增大,故B错误;
C.因为转速
n=3r/min=0.05r/s
所以转动周期为
T=s=20s
故C错误;
D.根据v=2πrn知,盾构机前端外边缘的线速度大小为
v=2×3.14×7.505×0.05m/s≈2.4m/s
故D正确。
故选AD。
17.
【详解】
某物体做匀速圆周运动,圆周的半径为R,周期为T,在运动的时间内,位移的大小
路程
运动的角速度
转过的角度是
18. 12 3.75 增大链轮和车轮半径,减小飞轮的半径。
【详解】
(1)飞轮的角速度与后轮的角速度相等,根据v=ωr得:
后轮的角速度与前轮相等为定值,即飞轮的角速度一定。由于
R链ω链=R飞ω飞
链轮的角速度与脚踏板的角速度相同,要想脚踏板的角速度最小,则飞轮的半径最小,链轮的半径最大;根据v=ωr得
(2)依据同带的瞬时速率相等,则有
R链ω链=R飞ω飞
而飞轮的角速度与后轮的角速度相等,因此车轮的速度
由此可见,在脚踩踏板的角速度一定时,要提高车速,就要增大链轮和车轮半径,减小飞轮的半径。
19.(1)3rad/s;(2)会滑落,0.86m
【详解】
(1)最大静摩擦力提供向心力有
μmg = mω2r
解得
ω = 3rad/s
(2)圆盘停下时,展品速度
vmax = ωr = 1.8m/s
展品在圆盘上做匀减速直线运动最大位移为
x = = 0.25m
展品在圆盘上做匀减速直线运动加速度满足
μmg = ma
物块运动到圆盘边沿时的速度v1满足
vmax2 - v12 = 2ax
解得
v1 = m/s > 0
可知展品会滑落
平抛运动时,竖直方向有
h = gt2
水平方向,落点距离抛点的水平距离
x1 = v1t = 0.36m
如图所示,则落点都转轴的水平距离为
L = = 0.86m
20.(1);(2)160N,方向沿路面向下
【详解】
(1)运动员受力如图
根据牛顿第二定律,可得
代入数据,解得
运动员所需向心力F=mgtan θ=450N
(2)当自行车速为,此时重力和支持力的合力不足以提供向心力,斜面对人和自行车施加沿斜面向下的静摩擦力,其受力分析如图所示
根据牛顿第二定律可得,在竖直方向有
在水平方向有
联立解得
21.(1)2N; (2)
【详解】
(1)由于小球在A处的速度大小为v,半径为R
则在A处时有
①
可得
在C处时,有
②
由①②式得
△F=F′-F=2mg=2 N
(2)在A处时板对小球的作用力为F,球做匀速圆周运动的向心力
F向=F+mg
由于无相对运动趋势,在B处不受摩擦力作用,受力分析如图所示。
则
作出的tan θ-F的关系图像如图所示
答案第1页,共2页
答案第1页,共2页
