4.1因式分解 课件(共21张PPT)
文档属性
| 名称 | 4.1因式分解 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 846.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 08:21:48 | ||
图片预览








文档简介
(共21张PPT)
北师大版八年级下册数学
第四章因式分解
4.1 因式分解
1.整式乘法有几种形式
2.乘法公式有哪些
(1)单项式乘以单项式
(2)单项式乘以多项式
(3)多项式乘以多项式
(1)平方差公式 (2)完全平方公式
复习引入
3.计算:
(1)3a(a-2b+c)
(2)(a+3)(a-3)
(3)(a+2b)2
(4)(a-3b)2
=3a2-6ab+3ac
=a2 - 9
=a2+4ab+4b2
=a2-6ab+9b2
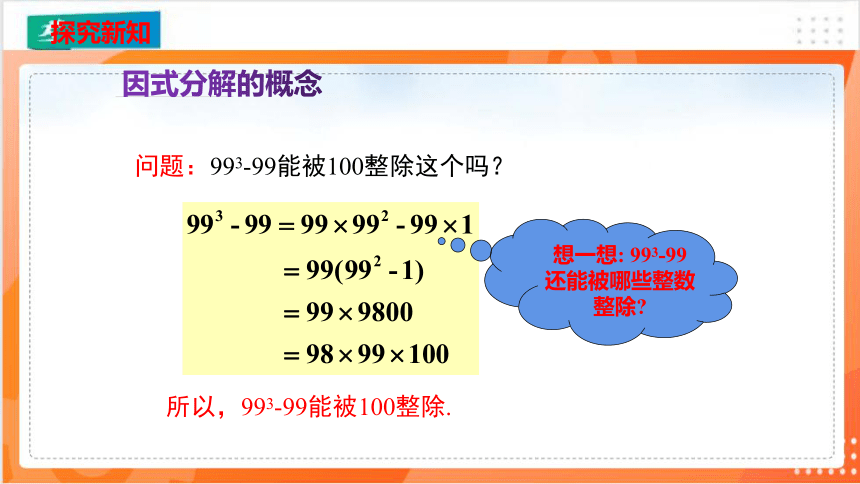
问题:993-99能被100整除这个吗?
所以,993-99能被100整除.
想一想: 993-99还能被哪些整数整除
因式分解的概念
探究新知
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
3x(x-1)= __,
m(a+b+c) = ______,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
答:由a(a+1)(a-1)得到a3-a的变形是
整式乘法,由a3-a得到a(a+1)(a-1)
的变形与上面的变形互为逆过程.
分解因式定义:
把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.
做一做
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
(1) 3x(x-1)= __,
(2) m(a+b+c) = ______ ,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
想一想:由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
由a(a+1)(a-1)得到a3-a的变形是整式乘法,
由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
因式分解与整式乘法的关系
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,右边是几个整式的乘积
想一想:整式乘法与因式分解有什么关系?
是互为相反的变形,即
例 若多项式x2+ax+b分解因式的结果为
a(x﹣2)(x+3),求a,b的值.
解:∵x2+ax+b=a(x﹣2)(x+3)
=ax2+ax-6a.
∴a=1,b=﹣6a=﹣6.
典例精析
方法归纳:对于此类问题,掌握因式分解与整式乘法为互逆运算是解题关键,应先把分解因式后的结果乘开,再与多项式的各项系数对应比较即可.
下列多项式中,分解因式的结果为-(x+y)(x-y)的是( )
A.x2﹣y2 B.﹣x2+y2
C.x2+y2 D.﹣x2﹣y2
B
练一练
1.计算下列各式:
(1)(a+b)(a-b)=__________;
(2)(a+b)2=______________;
(3)8y(y+1)=__________;
(4)a(x+y+1)=__________.
根据上面的算式将下列多项式进行因式分解:
(5)ax+ay+a; (6)a2-b2;
(7)a2+2ab+b2; (8)8y2+8y.
a2-b2
a2+2ab+b2
8y2+8y
ax+ay+a
课堂练习
(5)ax+ay+a=a(x+y+1).
(6)a2-b2=(a+b)(a-b).
(7)a2+2ab+b2=(a+b)2.
(8)8y2+8y=8y(y+1).
解:
2. 仔细阅读下面例题,解答问题:
例题:已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值.
解:设另一个因式为x+n,则
x2-4x+m=(x+3)(x+n),
即x2-4x+m=x2+(n+3)x+3n,
∴
故另一个因式为x-7,m的值为-21.
问题:仿照以上方法解答下面问题:
已知二次三项式2x2+3x-k有一个因式是2x-5,求另一个因式以及k的值.
设另一个因式为x+a,则
2x2+3x-k=(2x-5)(x+a),
即2x2+3x-k=2x2+(2a-5)x-5a,
∴
故另一个因式为x+4,k的值为20.
解:
3. 计算: 7652×17-2352 ×17
解: 7652×17-2352 ×17
=17(7652 -2352)=17(765+235)(765 -235)
=17 ×1000 ×530=9010000
4. 20042+2004能被2005整除吗
解: ∵20042+2004=2004(2004+1)
=2004 ×2005
∴ 20042+2004能被2005整除
因式分解
定义:把一个多项式化成几个整式的_____的形式,叫做因式分解,也可称为___________.
其中,每个整式叫做这个多项式的_______.
与多项式乘法运算的关系
的变形过程.
前者是把一个多项式化为几个整式的_____,后者是把几个整式的______化为一个_________.
积
分解因式
因式
相反
多项式
乘积
乘积
课堂小结
https://www.21cnjy.com/help/help_extract.php
北师大版八年级下册数学
第四章因式分解
4.1 因式分解
1.整式乘法有几种形式
2.乘法公式有哪些
(1)单项式乘以单项式
(2)单项式乘以多项式
(3)多项式乘以多项式
(1)平方差公式 (2)完全平方公式
复习引入
3.计算:
(1)3a(a-2b+c)
(2)(a+3)(a-3)
(3)(a+2b)2
(4)(a-3b)2
=3a2-6ab+3ac
=a2 - 9
=a2+4ab+4b2
=a2-6ab+9b2
问题:993-99能被100整除这个吗?
所以,993-99能被100整除.
想一想: 993-99还能被哪些整数整除
因式分解的概念
探究新知
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
3x(x-1)= __,
m(a+b+c) = ______,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
答:由a(a+1)(a-1)得到a3-a的变形是
整式乘法,由a3-a得到a(a+1)(a-1)
的变形与上面的变形互为逆过程.
分解因式定义:
把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.
做一做
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
(1) 3x(x-1)= __,
(2) m(a+b+c) = ______ ,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
想一想:由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
由a(a+1)(a-1)得到a3-a的变形是整式乘法,
由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
因式分解与整式乘法的关系
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,右边是几个整式的乘积
想一想:整式乘法与因式分解有什么关系?
是互为相反的变形,即
例 若多项式x2+ax+b分解因式的结果为
a(x﹣2)(x+3),求a,b的值.
解:∵x2+ax+b=a(x﹣2)(x+3)
=ax2+ax-6a.
∴a=1,b=﹣6a=﹣6.
典例精析
方法归纳:对于此类问题,掌握因式分解与整式乘法为互逆运算是解题关键,应先把分解因式后的结果乘开,再与多项式的各项系数对应比较即可.
下列多项式中,分解因式的结果为-(x+y)(x-y)的是( )
A.x2﹣y2 B.﹣x2+y2
C.x2+y2 D.﹣x2﹣y2
B
练一练
1.计算下列各式:
(1)(a+b)(a-b)=__________;
(2)(a+b)2=______________;
(3)8y(y+1)=__________;
(4)a(x+y+1)=__________.
根据上面的算式将下列多项式进行因式分解:
(5)ax+ay+a; (6)a2-b2;
(7)a2+2ab+b2; (8)8y2+8y.
a2-b2
a2+2ab+b2
8y2+8y
ax+ay+a
课堂练习
(5)ax+ay+a=a(x+y+1).
(6)a2-b2=(a+b)(a-b).
(7)a2+2ab+b2=(a+b)2.
(8)8y2+8y=8y(y+1).
解:
2. 仔细阅读下面例题,解答问题:
例题:已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值.
解:设另一个因式为x+n,则
x2-4x+m=(x+3)(x+n),
即x2-4x+m=x2+(n+3)x+3n,
∴
故另一个因式为x-7,m的值为-21.
问题:仿照以上方法解答下面问题:
已知二次三项式2x2+3x-k有一个因式是2x-5,求另一个因式以及k的值.
设另一个因式为x+a,则
2x2+3x-k=(2x-5)(x+a),
即2x2+3x-k=2x2+(2a-5)x-5a,
∴
故另一个因式为x+4,k的值为20.
解:
3. 计算: 7652×17-2352 ×17
解: 7652×17-2352 ×17
=17(7652 -2352)=17(765+235)(765 -235)
=17 ×1000 ×530=9010000
4. 20042+2004能被2005整除吗
解: ∵20042+2004=2004(2004+1)
=2004 ×2005
∴ 20042+2004能被2005整除
因式分解
定义:把一个多项式化成几个整式的_____的形式,叫做因式分解,也可称为___________.
其中,每个整式叫做这个多项式的_______.
与多项式乘法运算的关系
的变形过程.
前者是把一个多项式化为几个整式的_____,后者是把几个整式的______化为一个_________.
积
分解因式
因式
相反
多项式
乘积
乘积
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
