2.4用单摆测量重力加速度 同步练习(Word版含答案)
文档属性
| 名称 | 2.4用单摆测量重力加速度 同步练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 973.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-15 00:00:00 | ||
图片预览



文档简介
2.4用单摆测量重力加速度同步练习2021—2022学年高中物理粤教版(2019)选择性必修第一册
一、选择题(共15题)
1.在一次做“探究单摆周期T与摆长L的关系”实验中,在测量单摆周期时,摆球通过最低点时开始计时并记数为0次,则到摆球第N次通过最低点所用时间为t,摆线长度为l,某同学根据测量数据绘制出图像如图所示,则下列说法正确的是( )
A.摆球直径 B.单摆周期的平方()与摆线长度l成正比。
C.当地重力加速度大小为 D.当地重力加速度大小为
2.某同学做“用单摆测定重力加速度”的实验时,测得的重力加速度数值明显大于当地的重力加速度的实际值.造成这一情况的可能原因是( )
A.测量摆长时,把悬挂状态的摆线长当成摆长
B.测量周期时,当摆球通过平衡位置时启动秒表,此后摆球第30次通过平衡位置时制动秒表,读出经历的时间为t,并由计算式求得周期
C.开始摆动时振幅过小
D.所用摆球的质量过大
3.在用单摆测量重力加速度的实验中,用多组实验数据做出周期(T)的平方和摆长(L)的T2-L图线,可以求出重力加速度g。已知两位同学做出的T2-L图线如图中的a、b所示,其中a和b平行,图线a对应的g值很接近当地重力加速度的值。相对于图线a,关于图线b的分析正确的是( )
A.可能是误将绳长记为摆长L
B.可能是误将悬点到小球下端的距离记为摆长L
C.可能是误将49次全振动记为50次
D.根据图线b不能准确测出当地的重力加速度
4.在“探究单摆周期与摆长的关系”的实验中,关于摆长和周期的测量,下列说法正确的是( )
A.摆长等于摆线长度加上球的直径
B.测量周期时只要测量一次全振动的时间
C.测量时间应从摆球经过平衡位置开始计时
D.测量时间应从摆球经过最高点开始计时
5.在利用单摆测定重力加速度的实验中,下列说法正确的是
A.把单摆从平衡位置拉开的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
6.利用单摆测定重力加速度g时,下列情况中会导致所测得的g值偏大的是( )
A.小球质量过大
B.摆线太长
C.把悬线长和小球直径之和当作摆长
D.把悬线长当作摆长
7.下列关于单摆实验过程的具体步骤中,你觉得存在明显问题的是( )
A.将细线穿过金属小球上的小孔,在细线的一端打一个稍大一点的结,制成一个单摆
B.将单摆平躺在桌上,用刻度尺、游标卡尺分别测量摆线长度和直径,取半径加线长为摆长
C.铁架台放在桌边,使固定的铁架伸出桌面,然后把单摆固定在铁夹上,使摆球自由下垂
D.当摆动稳定后摆球经过最低点时开始计时,测30~50次全振动的时间,并求出周期
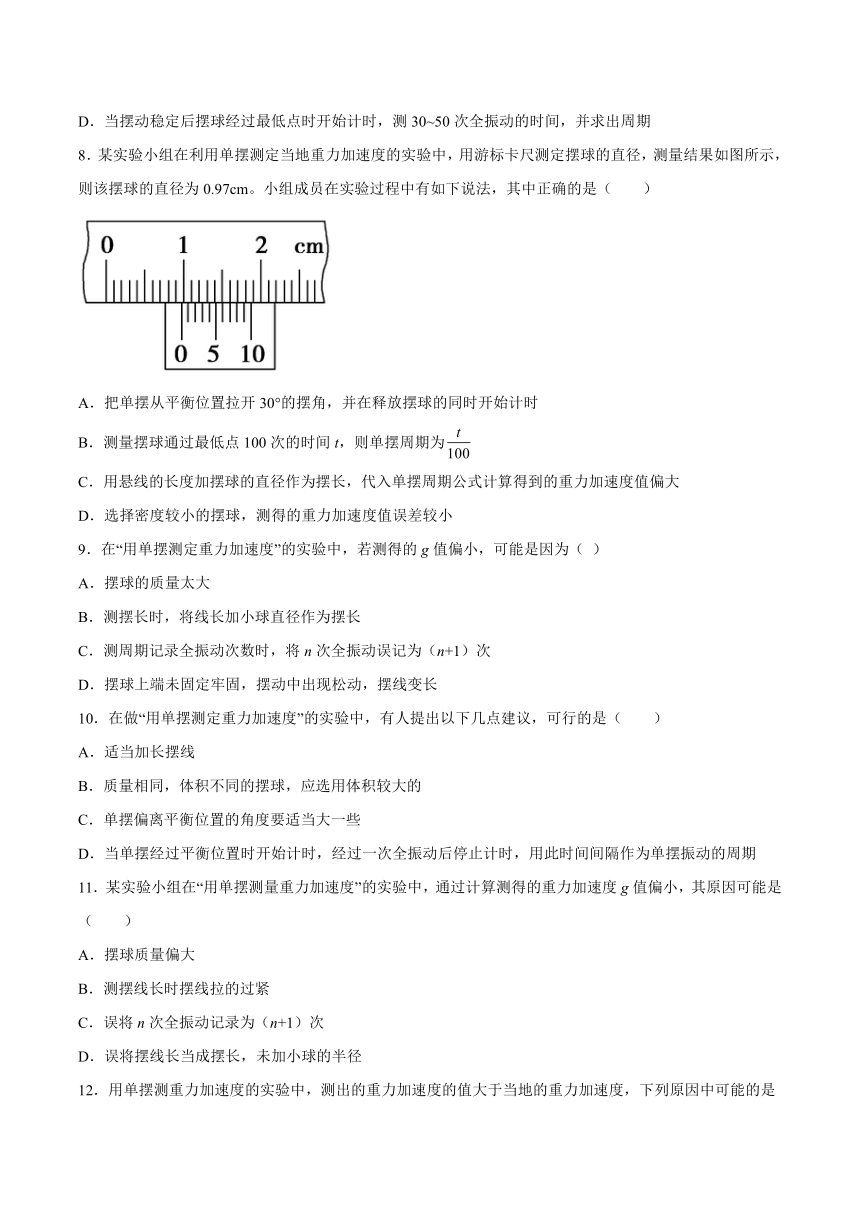
8.某实验小组在利用单摆测定当地重力加速度的实验中,用游标卡尺测定摆球的直径,测量结果如图所示,则该摆球的直径为0.97cm。小组成员在实验过程中有如下说法,其中正确的是( )
A.把单摆从平衡位置拉开30°的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
9.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
10.在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议,可行的是( )
A.适当加长摆线
B.质量相同,体积不同的摆球,应选用体积较大的
C.单摆偏离平衡位置的角度要适当大一些
D.当单摆经过平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆振动的周期
11.某实验小组在“用单摆测量重力加速度”的实验中,通过计算测得的重力加速度g值偏小,其原因可能是( )
A.摆球质量偏大
B.测摆线长时摆线拉的过紧
C.误将n次全振动记录为(n+1)次
D.误将摆线长当成摆长,未加小球的半径
12.用单摆测重力加速度的实验中,测出的重力加速度的值大于当地的重力加速度,下列原因中可能的是( )
A.振幅太小导致测得的周期偏小
B.计算摆长时,只考虑线长,没有加上摆球半径
C.将n次全振动误记为(n-1)次全振动
D.将n次全振动误记为(n+1)次全振动
13.马玲同学周末用单摆测当地的重力加速度,将单摆固定好,用米尺测绳长,用游标卡尺测摆球直径,用秒表测出50个周期的时间然后算出周期T。改变摆长l,重复实验,得到多组实验数据后,在坐标纸上做出如图所示的图像。下列叙述正确的是( )
A.图像不过原点的原因可能是误将绳长加摆球直径当成摆长
B.如果马玲同学把绳长当成了摆长(没加摆球半径),则用此图像算出的重力加速度偏小
C.如果马玲同学把绳长当成了摆长(没加摆球半径),则用此图像算出的重力加速度不受影响
D.图像的斜率等于重力加速度
14.某同学在做“用单摆测定重力加速度”的实验时,如果测得的g值偏小,可能的原因是( )
A.将摆线长加球的直径当作摆长
B.实验中误将31次全振动计为30次全振动
C.结束计时时,提前按秒表
D.小球做圆锥摆运动
15.放在实验室里位置不变的单摆,若摆长不变,摆球的质量增加为原来的4倍,摆球经过平衡位置时的速度减小为原来的一半,则单摆摆动的( )
A.振幅变小 B.振幅变大 C.频率变小 D.频率变大
二、填空题(共4题)
16.科学探险队员探究珠穆朗玛峰山脚与山顶重力加速度的差值。在山脚处,他用一个小铁球与一条细线、支架组成一个单摆装置,通过改变摆长L,测出相应单摆的周期T,用测出的L与T的值,作出了T2-L图像如图中直线c所示。当他成功攀登到山顶后,他又重复了在山脚做的实验。并用L与T的测量值在同一坐标系中作出了另一条T2-L图像。则利用山顶实验数据作出的图线可能是图中的直线_____;在山脚做实验测摆长时若没加小球的半径。作出的图线可能是直线______;测摆长时没加小球半径,用测量数据通过作T2-L图像测出的重力加速度值____(“偏大”“偏小”或“不变”)
17.在“用单摆测定重力加速度”的实验中,某同学测出多组摆长L与周期T的数据,并输入计算机生成如图所示的T2-L图像,计算机显示图线的斜率为k,根据T2-L图像__________(填写“能”或“不能”)求出当地的重力加速度,如填写“能”,写出重力加速度的表达式g=__________。
18.某同学在做“利用单摆测重力加速度”实验。某次用刻度尺测得摆线长为67.80cm。用游标卡尺测得小球直径的读数如图甲所示,则小球直径为______cm;重复实验几次,改变摆线的长度L,用秒表测出相应的周期T,再以L为横坐标,为纵坐标作图,对应的图像应为图乙中的直线_____(填“1”、“2”或“3” )。若已知直线的斜率为k,请写出重力加速度g的表达式 _____________;
19.(1)新新和华华在做“探究单摆周期与摆长的关系”实验中
①将摆球悬挂于铁架台上,甲图中悬挂方式正确的是__________;测量小球直径时游标卡尺如图乙所示,其读数为____________mm;
②测单摆周期时,当摆球经过____________时开始计时并计1次,测出经过该位置N次所用时间为t,则单摆周期为T=______________;
三、综合题(共4题)
20.已知月球表面的重力加速度是地球的,如果把一个周期为8s的单摆放到月球上,它的周期变为多少?
21.在用单摆测量重力加速度的实验中,测得悬线长为l,摆球直径为d,完成n次完整振动所用时间为t,求重力加速度g。
22.单摆是常见的一种简谐运动,如图所示。已知质量为m的摆球,摆长为l,完成N次全振动的时间是t,请根据以上数据完成以下问题:
(1)画出摆角为θ时,小球的受力图,并求出此刻回复力的大小和方向(可在图中画出);
(2)当地重力加速度g是多大;
(3)很多同学认为直接测量一次全振动时间既简单又节省时间,你同意这个观点吗?请简要分析说明。
23.在生活中寻找摆钟(若找不到实物,可以上网搜索摆钟的相关资料),撰写小论文论述摆钟的构造及计时原理。
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.C
5.C
6.C
7.B
8.C
9.D
10.A
11.D
12.D
13.C
14.B
15.A
16. a b 不变
17. 能
18. 2.16 1
19. C 20.6 最低位置
20.19.6s
21.
22.
(1)摆角为θ时,小球的受力图如图
回复力为
回复力方向如图所示
(2)由题意可知,单摆的周期为
根据单摆周期公式可得
联立解得
(3)不同意,因为多次测量利用累计法可以减小测量误差。
23.
钟摆的原理是根据单摆周期公式制成的,其主要构造如图;其主要部分是擒纵机构;擒纵机构是一种机械能量传递的开关装置,这个开关受“计时基准”的控制,以一定的频率开关钟表的主传动链,是指示停-动相间并一定的平均速度转动,从而指示准确的时间;擒纵结构的功能可以从两方面理解:擒,将主动传动的运动锁住(擒住),此时钟表的主动链是锁定的;纵,就是以震荡系统的一部分势能,开启(放开)主传动链运动,同时从主传动链中取回一定的能量,以维持震荡系统的工作;擒纵机构是现代机械钟表的核心,最初的擒纵机构诞生于15世纪,之后逐渐进化到现在的各种样子,目前,仍有数百种擒纵机构在现代钟表中使用。
答案第1页,共2页
一、选择题(共15题)
1.在一次做“探究单摆周期T与摆长L的关系”实验中,在测量单摆周期时,摆球通过最低点时开始计时并记数为0次,则到摆球第N次通过最低点所用时间为t,摆线长度为l,某同学根据测量数据绘制出图像如图所示,则下列说法正确的是( )
A.摆球直径 B.单摆周期的平方()与摆线长度l成正比。
C.当地重力加速度大小为 D.当地重力加速度大小为
2.某同学做“用单摆测定重力加速度”的实验时,测得的重力加速度数值明显大于当地的重力加速度的实际值.造成这一情况的可能原因是( )
A.测量摆长时,把悬挂状态的摆线长当成摆长
B.测量周期时,当摆球通过平衡位置时启动秒表,此后摆球第30次通过平衡位置时制动秒表,读出经历的时间为t,并由计算式求得周期
C.开始摆动时振幅过小
D.所用摆球的质量过大
3.在用单摆测量重力加速度的实验中,用多组实验数据做出周期(T)的平方和摆长(L)的T2-L图线,可以求出重力加速度g。已知两位同学做出的T2-L图线如图中的a、b所示,其中a和b平行,图线a对应的g值很接近当地重力加速度的值。相对于图线a,关于图线b的分析正确的是( )
A.可能是误将绳长记为摆长L
B.可能是误将悬点到小球下端的距离记为摆长L
C.可能是误将49次全振动记为50次
D.根据图线b不能准确测出当地的重力加速度
4.在“探究单摆周期与摆长的关系”的实验中,关于摆长和周期的测量,下列说法正确的是( )
A.摆长等于摆线长度加上球的直径
B.测量周期时只要测量一次全振动的时间
C.测量时间应从摆球经过平衡位置开始计时
D.测量时间应从摆球经过最高点开始计时
5.在利用单摆测定重力加速度的实验中,下列说法正确的是
A.把单摆从平衡位置拉开的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
6.利用单摆测定重力加速度g时,下列情况中会导致所测得的g值偏大的是( )
A.小球质量过大
B.摆线太长
C.把悬线长和小球直径之和当作摆长
D.把悬线长当作摆长
7.下列关于单摆实验过程的具体步骤中,你觉得存在明显问题的是( )
A.将细线穿过金属小球上的小孔,在细线的一端打一个稍大一点的结,制成一个单摆
B.将单摆平躺在桌上,用刻度尺、游标卡尺分别测量摆线长度和直径,取半径加线长为摆长
C.铁架台放在桌边,使固定的铁架伸出桌面,然后把单摆固定在铁夹上,使摆球自由下垂
D.当摆动稳定后摆球经过最低点时开始计时,测30~50次全振动的时间,并求出周期
8.某实验小组在利用单摆测定当地重力加速度的实验中,用游标卡尺测定摆球的直径,测量结果如图所示,则该摆球的直径为0.97cm。小组成员在实验过程中有如下说法,其中正确的是( )
A.把单摆从平衡位置拉开30°的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
9.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
10.在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议,可行的是( )
A.适当加长摆线
B.质量相同,体积不同的摆球,应选用体积较大的
C.单摆偏离平衡位置的角度要适当大一些
D.当单摆经过平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆振动的周期
11.某实验小组在“用单摆测量重力加速度”的实验中,通过计算测得的重力加速度g值偏小,其原因可能是( )
A.摆球质量偏大
B.测摆线长时摆线拉的过紧
C.误将n次全振动记录为(n+1)次
D.误将摆线长当成摆长,未加小球的半径
12.用单摆测重力加速度的实验中,测出的重力加速度的值大于当地的重力加速度,下列原因中可能的是( )
A.振幅太小导致测得的周期偏小
B.计算摆长时,只考虑线长,没有加上摆球半径
C.将n次全振动误记为(n-1)次全振动
D.将n次全振动误记为(n+1)次全振动
13.马玲同学周末用单摆测当地的重力加速度,将单摆固定好,用米尺测绳长,用游标卡尺测摆球直径,用秒表测出50个周期的时间然后算出周期T。改变摆长l,重复实验,得到多组实验数据后,在坐标纸上做出如图所示的图像。下列叙述正确的是( )
A.图像不过原点的原因可能是误将绳长加摆球直径当成摆长
B.如果马玲同学把绳长当成了摆长(没加摆球半径),则用此图像算出的重力加速度偏小
C.如果马玲同学把绳长当成了摆长(没加摆球半径),则用此图像算出的重力加速度不受影响
D.图像的斜率等于重力加速度
14.某同学在做“用单摆测定重力加速度”的实验时,如果测得的g值偏小,可能的原因是( )
A.将摆线长加球的直径当作摆长
B.实验中误将31次全振动计为30次全振动
C.结束计时时,提前按秒表
D.小球做圆锥摆运动
15.放在实验室里位置不变的单摆,若摆长不变,摆球的质量增加为原来的4倍,摆球经过平衡位置时的速度减小为原来的一半,则单摆摆动的( )
A.振幅变小 B.振幅变大 C.频率变小 D.频率变大
二、填空题(共4题)
16.科学探险队员探究珠穆朗玛峰山脚与山顶重力加速度的差值。在山脚处,他用一个小铁球与一条细线、支架组成一个单摆装置,通过改变摆长L,测出相应单摆的周期T,用测出的L与T的值,作出了T2-L图像如图中直线c所示。当他成功攀登到山顶后,他又重复了在山脚做的实验。并用L与T的测量值在同一坐标系中作出了另一条T2-L图像。则利用山顶实验数据作出的图线可能是图中的直线_____;在山脚做实验测摆长时若没加小球的半径。作出的图线可能是直线______;测摆长时没加小球半径,用测量数据通过作T2-L图像测出的重力加速度值____(“偏大”“偏小”或“不变”)
17.在“用单摆测定重力加速度”的实验中,某同学测出多组摆长L与周期T的数据,并输入计算机生成如图所示的T2-L图像,计算机显示图线的斜率为k,根据T2-L图像__________(填写“能”或“不能”)求出当地的重力加速度,如填写“能”,写出重力加速度的表达式g=__________。
18.某同学在做“利用单摆测重力加速度”实验。某次用刻度尺测得摆线长为67.80cm。用游标卡尺测得小球直径的读数如图甲所示,则小球直径为______cm;重复实验几次,改变摆线的长度L,用秒表测出相应的周期T,再以L为横坐标,为纵坐标作图,对应的图像应为图乙中的直线_____(填“1”、“2”或“3” )。若已知直线的斜率为k,请写出重力加速度g的表达式 _____________;
19.(1)新新和华华在做“探究单摆周期与摆长的关系”实验中
①将摆球悬挂于铁架台上,甲图中悬挂方式正确的是__________;测量小球直径时游标卡尺如图乙所示,其读数为____________mm;
②测单摆周期时,当摆球经过____________时开始计时并计1次,测出经过该位置N次所用时间为t,则单摆周期为T=______________;
三、综合题(共4题)
20.已知月球表面的重力加速度是地球的,如果把一个周期为8s的单摆放到月球上,它的周期变为多少?
21.在用单摆测量重力加速度的实验中,测得悬线长为l,摆球直径为d,完成n次完整振动所用时间为t,求重力加速度g。
22.单摆是常见的一种简谐运动,如图所示。已知质量为m的摆球,摆长为l,完成N次全振动的时间是t,请根据以上数据完成以下问题:
(1)画出摆角为θ时,小球的受力图,并求出此刻回复力的大小和方向(可在图中画出);
(2)当地重力加速度g是多大;
(3)很多同学认为直接测量一次全振动时间既简单又节省时间,你同意这个观点吗?请简要分析说明。
23.在生活中寻找摆钟(若找不到实物,可以上网搜索摆钟的相关资料),撰写小论文论述摆钟的构造及计时原理。
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.C
5.C
6.C
7.B
8.C
9.D
10.A
11.D
12.D
13.C
14.B
15.A
16. a b 不变
17. 能
18. 2.16 1
19. C 20.6 最低位置
20.19.6s
21.
22.
(1)摆角为θ时,小球的受力图如图
回复力为
回复力方向如图所示
(2)由题意可知,单摆的周期为
根据单摆周期公式可得
联立解得
(3)不同意,因为多次测量利用累计法可以减小测量误差。
23.
钟摆的原理是根据单摆周期公式制成的,其主要构造如图;其主要部分是擒纵机构;擒纵机构是一种机械能量传递的开关装置,这个开关受“计时基准”的控制,以一定的频率开关钟表的主传动链,是指示停-动相间并一定的平均速度转动,从而指示准确的时间;擒纵结构的功能可以从两方面理解:擒,将主动传动的运动锁住(擒住),此时钟表的主动链是锁定的;纵,就是以震荡系统的一部分势能,开启(放开)主传动链运动,同时从主传动链中取回一定的能量,以维持震荡系统的工作;擒纵机构是现代机械钟表的核心,最初的擒纵机构诞生于15世纪,之后逐渐进化到现在的各种样子,目前,仍有数百种擒纵机构在现代钟表中使用。
答案第1页,共2页
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
