苏科版七年级数学下册 7.5 多边形的内角和与外角和(第2课时) 教案
文档属性
| 名称 | 苏科版七年级数学下册 7.5 多边形的内角和与外角和(第2课时) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 00:00:00 | ||
图片预览

文档简介
7.5 多边形的内角和与外角和(2)教学设计
(苏科版教材七年级下册)
[教学目标]:
1、了解多边形的有关概念,认识多边形的边、内角、顶点、对角线。
2、经历探索多边形的内角和公式的过程,了解多边形的内角和公式,进一步发展学生的合情推理意识,主动探究的习惯,体会数学与现实世界的紧密联系。
3、会用多边形的内角和公式进行简单的计算与说理。
4、进一步体会化归、类比、转化、由特殊到一般等数学思想方法。
[教学重点]:
1、多边形内角和公式的推导及应用。
2、引导学生经历探究过程,并能进行简单的说理。
[教学难点]:多边形内角和公式的推导。
[教学过程]:
板块一:从三角形到多边形
生活数学
问题1:由下列图形你能抽象出什么几何图形?
让学生观察生活图片,了解生活中除了三角形还有其他一些几何图形,从而引出多边形的概念。(板书:多边形)
2、概念建构
问题2:三角形是怎么定义的?
指名答,出示定义。
问题3:你能仿照三角形的定义给多边形下个定义吗?
指名答,出示定义,完善定义。
3、概念补充
引导学生认识与之相关的一些小概念(顶点、边、内角、对角线。)
经验类比
问题4:学习了三角形的概念后,我们是如何继续研究三角形的?
指名答:继续研究三角形的性质。
问题5:三角形的性质,我们是从哪几个方面展开研究的?
指名答:三角形的角和边
问题6:学习了多边形的概念后,我们将如何继续研究多边形?
指名答:研究多边形的内角和
教师板书课题。
板块二:探索四边形的内角和
问题1:三角形的内角和是多少度?我们是怎么得来的?
(板书:三角形 180°)
小学:用剪拼法发现得来
中学:用平行线的知识证明得来
教师说明进入中学后学习的要求更高了,对于发现的结论需要进行说理证明。
问题2:长方形的内角和是多少度?你怎么得到的?
4个90°
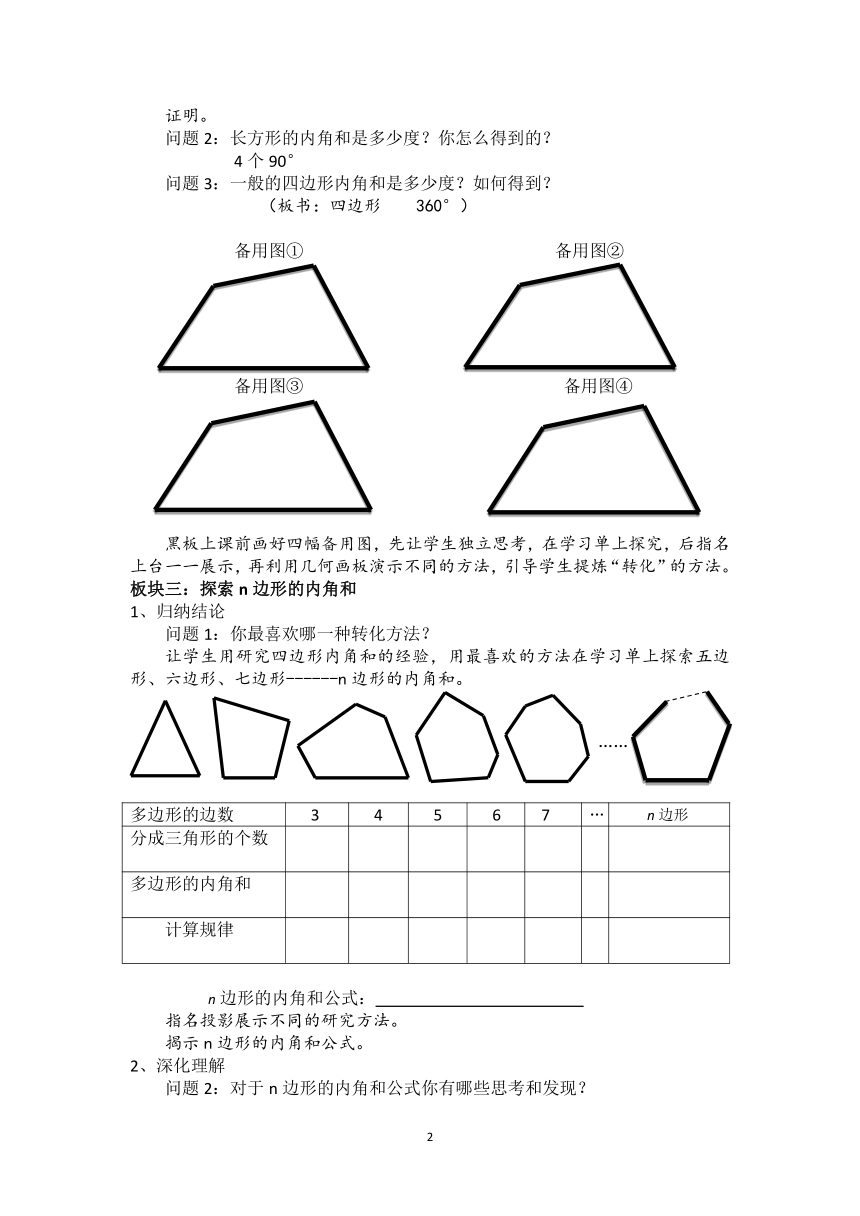
问题3:一般的四边形内角和是多少度?如何得到?
(板书:四边形 360°)
备用图① 备用图②
备用图③ 备用图④
黑板上课前画好四幅备用图,先让学生独立思考,在学习单上探究,后指名上台一一展示,再利用几何画板演示不同的方法,引导学生提炼“转化”的方法。
板块三:探索n边形的内角和
1、归纳结论
问题1:你最喜欢哪一种转化方法?
让学生用研究四边形内角和的经验,用最喜欢的方法在学习单上探索五边形、六边形、七边形------n边形的内角和。
……
多边形的边数 3 4 5 6 7 … n边形
分成三角形的个数
多边形的内角和
计算规律
n边形的内角和公式:
指名投影展示不同的研究方法。
揭示n边形的内角和公式。
2、深化理解
问题2:对于n边形的内角和公式你有哪些思考和发现?
让同桌先交流,后指名回答:由边数可求内角和;由内角和可求边数;边数增加1,内角和也就增加180°;内角和一定是180°的倍数。
板块四:多边形内角和的应用
学以致用
例1:一个多边形的内角和为1080°,这个多边形是几边形?
指名回答解题方法,后学生独立完成,教师投影展示解题完整过程。
例2:如图,在四边形ABCD中,如果∠A与∠C互补,那么它的另一组对角∠B与∠D有什么关系?为什么?
指名学生说理,课件出示完整说理过程。
并引导学生总结:四边形中如果一组对角互补,
那么另外一组对角也互补。
拓展:如图,在四边形ABCD中,∠A与∠C互补,∠ABC、 ∠ADC的平分线分别交CD、AB于点E、F。 ∠ 1与∠ 2有怎样的数量关系?为什么?
同桌先议一议、说一说,指名说,后要求学生一起看书P31.
练习巩固
问题1:填空和选择
(1)、一个多边形的内角和不可能是( )
A、1800° B、360° C、1000° D、900°
(2)、10边形的内角和是______度;
(3)、某6边形的内角都相等,则每个内角为______度;
(4)、n+1边形的内角和比n边形的内角和大____度。
先让学生独立完成,后指名分析。
问题2:求下列图形中 x的值
先让学生独立练习,后指名在白板上书写、讲解。
板块五:小结与思考
问题1:本节课的学习我们经历了怎样的过程?
问题2:在本节课中你获得了哪些学习方法?你还有哪些困惑?
问题3:你能结合本课的学习提出一个问题吗?
先出示三个问题,要求前后桌四人一组分享和交流,后指名说。教师提炼总结。
板块六:课后作业
阅读:课本P30-31相关内容
必做:课本习题7.5的6、7、8
选做:撰写感悟小文章
A
B
C
D
2x°
150°
140°°
120°
90°
x°
x°
x°
(苏科版教材七年级下册)
[教学目标]:
1、了解多边形的有关概念,认识多边形的边、内角、顶点、对角线。
2、经历探索多边形的内角和公式的过程,了解多边形的内角和公式,进一步发展学生的合情推理意识,主动探究的习惯,体会数学与现实世界的紧密联系。
3、会用多边形的内角和公式进行简单的计算与说理。
4、进一步体会化归、类比、转化、由特殊到一般等数学思想方法。
[教学重点]:
1、多边形内角和公式的推导及应用。
2、引导学生经历探究过程,并能进行简单的说理。
[教学难点]:多边形内角和公式的推导。
[教学过程]:
板块一:从三角形到多边形
生活数学
问题1:由下列图形你能抽象出什么几何图形?
让学生观察生活图片,了解生活中除了三角形还有其他一些几何图形,从而引出多边形的概念。(板书:多边形)
2、概念建构
问题2:三角形是怎么定义的?
指名答,出示定义。
问题3:你能仿照三角形的定义给多边形下个定义吗?
指名答,出示定义,完善定义。
3、概念补充
引导学生认识与之相关的一些小概念(顶点、边、内角、对角线。)
经验类比
问题4:学习了三角形的概念后,我们是如何继续研究三角形的?
指名答:继续研究三角形的性质。
问题5:三角形的性质,我们是从哪几个方面展开研究的?
指名答:三角形的角和边
问题6:学习了多边形的概念后,我们将如何继续研究多边形?
指名答:研究多边形的内角和
教师板书课题。
板块二:探索四边形的内角和
问题1:三角形的内角和是多少度?我们是怎么得来的?
(板书:三角形 180°)
小学:用剪拼法发现得来
中学:用平行线的知识证明得来
教师说明进入中学后学习的要求更高了,对于发现的结论需要进行说理证明。
问题2:长方形的内角和是多少度?你怎么得到的?
4个90°
问题3:一般的四边形内角和是多少度?如何得到?
(板书:四边形 360°)
备用图① 备用图②
备用图③ 备用图④
黑板上课前画好四幅备用图,先让学生独立思考,在学习单上探究,后指名上台一一展示,再利用几何画板演示不同的方法,引导学生提炼“转化”的方法。
板块三:探索n边形的内角和
1、归纳结论
问题1:你最喜欢哪一种转化方法?
让学生用研究四边形内角和的经验,用最喜欢的方法在学习单上探索五边形、六边形、七边形------n边形的内角和。
……
多边形的边数 3 4 5 6 7 … n边形
分成三角形的个数
多边形的内角和
计算规律
n边形的内角和公式:
指名投影展示不同的研究方法。
揭示n边形的内角和公式。
2、深化理解
问题2:对于n边形的内角和公式你有哪些思考和发现?
让同桌先交流,后指名回答:由边数可求内角和;由内角和可求边数;边数增加1,内角和也就增加180°;内角和一定是180°的倍数。
板块四:多边形内角和的应用
学以致用
例1:一个多边形的内角和为1080°,这个多边形是几边形?
指名回答解题方法,后学生独立完成,教师投影展示解题完整过程。
例2:如图,在四边形ABCD中,如果∠A与∠C互补,那么它的另一组对角∠B与∠D有什么关系?为什么?
指名学生说理,课件出示完整说理过程。
并引导学生总结:四边形中如果一组对角互补,
那么另外一组对角也互补。
拓展:如图,在四边形ABCD中,∠A与∠C互补,∠ABC、 ∠ADC的平分线分别交CD、AB于点E、F。 ∠ 1与∠ 2有怎样的数量关系?为什么?
同桌先议一议、说一说,指名说,后要求学生一起看书P31.
练习巩固
问题1:填空和选择
(1)、一个多边形的内角和不可能是( )
A、1800° B、360° C、1000° D、900°
(2)、10边形的内角和是______度;
(3)、某6边形的内角都相等,则每个内角为______度;
(4)、n+1边形的内角和比n边形的内角和大____度。
先让学生独立完成,后指名分析。
问题2:求下列图形中 x的值
先让学生独立练习,后指名在白板上书写、讲解。
板块五:小结与思考
问题1:本节课的学习我们经历了怎样的过程?
问题2:在本节课中你获得了哪些学习方法?你还有哪些困惑?
问题3:你能结合本课的学习提出一个问题吗?
先出示三个问题,要求前后桌四人一组分享和交流,后指名说。教师提炼总结。
板块六:课后作业
阅读:课本P30-31相关内容
必做:课本习题7.5的6、7、8
选做:撰写感悟小文章
A
B
C
D
2x°
150°
140°°
120°
90°
x°
x°
x°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
