苏科版七年级数学下册 9.4 乘法公式(微专题:在几何图形中的拓展应用)教案
文档属性
| 名称 | 苏科版七年级数学下册 9.4 乘法公式(微专题:在几何图形中的拓展应用)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 00:00:00 | ||
图片预览


文档简介
微专题:乘法公式在几何图形中的拓展应用
从课本出发:1. 完全平方公式:a2±2ab+b2=(a±b)2
2.平方差公式:a2-b2=(a+b)(a-b)
类型一:完全平方公式与图形面积
问题一:通常情况下,用两种不同的方法计算同一图形的面积,可以得到一个恒等式,
①如图1,用4块完全相同的长方形围成一个正方形.根据图中阴影部分的面积可表示为__________,还可表示为___________,可以得到的恒等式是___________.
②类似地,用两种不同的方法计算同一各几何体的体积,也可以得到一个恒等式,如图2是边长为的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
应用:1.如图为某正方形的房屋结构平面图,其中主卧与客卧都为正方形,其面积之和比其余面积(阴影部分)多2.25平方米,则主卧与客卧的周长差为( )
A.12米 B.10米 C.8米 D.6米
2.如图所示,将一张长方形纸板按图中虚线裁剪成九块,若图中①②都是剪成边为a的大正方形,③④都是剪成边长为b的小正方形,⑤⑥⑦⑧⑨都是剪成边长分别为a、b的小长方形﹒
(1)观察图形,可以发现多项式2a2+5ab+2b2可以因式分解为____________________;
(2)若每块小长方形的的面积为3cm2,四个正方形的面积之和为38cm2,试求图中所有裁剪线(虚线部分)长之和﹒
﹒
3.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
类型二: 平方差公式与图形面积
问题二:通常情况下用两种不同的方法计算同一个图形的面积,可以得到一个恒等式。类似地。
(1)如图①,在边长为a的正方形纸片上剪去一个边长为b(b方法①________________________________;方法②________________________________;
由此可以验证的乘法公式是___.
(2)类似地,在边长为a的正方体上割去一个边长为b(b方法①________________________________;方法②________________________________;
由此可以得到的等式是________________________________,并证明这个等式.
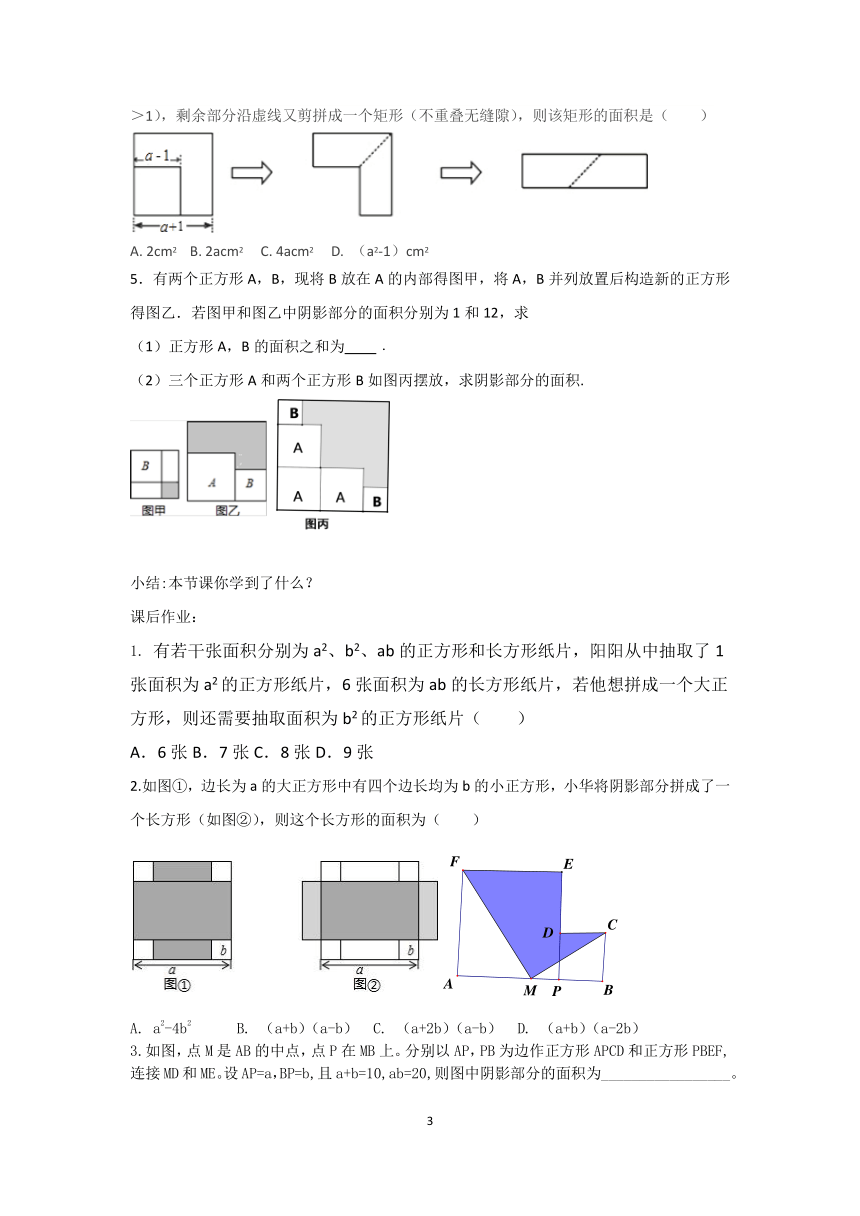
应用:4.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
A. 2cm2 B. 2acm2 C. 4acm2 D. (a2-1)cm2
5.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,求
(1)正方形A,B的面积之和为 ﹒
(2)三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
小结:本节课你学到了什么?
课后作业:
1. 有若干张面积分别为a2、b2、ab的正方形和长方形纸片,阳阳从中抽取了1张面积为a2的正方形纸片,6张面积为ab的长方形纸片,若他想拼成一个大正方形,则还需要抽取面积为b2的正方形纸片( )
A.6张B.7张C.8张D.9张
2.如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为( )
A. a2-4b2 B. (a+b)(a-b) C. (a+2b)(a-b) D. (a+b)(a-2b)
3.如图,点M是AB的中点,点P在MB上。分别以AP,PB为边作正方形APCD和正方形PBEF,连接MD和ME。设AP=a,BP=b,且a+b=10,ab=20,则图中阴影部分的面积为_________________。
4.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,测得的线段长度如图所示,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子.
(1)用含有a,b的代数式表示该长方体盒子的体积,并化简.
(2)若a=12,b=2,求此长方体盒子的体积.
5. 小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=25,ab=12,求小红家这块L形菜地的面积.
6.我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:
就可以用如图所示的面积关系来说明。
(1)请根据如图写出代数恒等式,并根据所写恒等式计算:
(2)若求的值;
(3)现有如图中的彩色卡片:A型、B型、C型,把这些卡片不重叠不留缝隙地贴在棱长为的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用
7.(阅读理解)
“若满足,求的值”
解:设,则,
所以
(解决问题)
(1)若满足,求的值.
(2)若满足,求的值.
(3)如图,正方形的边长为,,长方形的面积是500,四边形和都是正方形,是长方形,求图中阴影部分的面积。
8.一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.
9.如图是一个长为、宽为的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
(1)如图中的阴影部分面积为: ;(用、的代数式表示)
(2)观察如图,请你写出、、之间的等量关系是 ;
(3)根据(2)中的结论,若,,则 ;
(4)实际上通过计算图形的阴影可以探求相应的等式,如图,请你写出这个等式 ;
(5)如图,线段 (其中为正数),点线在段上,在线段同侧作正方形及正方形,连接,,得到.当时,的面积记为;当时,的面积记为;当时,的面积记为;当时,的面积记为,则 .
10.借助图形直观,感受数与形之间的关系,我们常常可以发现一些重要结论.
初步应用 (1)①如图1,大长方形的面积可以看成4个小长方形的面积之和,由此得到多项式乘多项式的运算法,则______(用图中字母表示)
②如图2,借助①,写出一个我们学过的公式:______(用图中字母表示)
深入探究 (2)仿照图2,构造图形并计算(a+b+c)2
拓展延伸 借助以上探究经验,解决下列问题:(3)①代数式(a1+a2+a2+a3+a4+a5)2展开、合并同类项后,得到的多项式的项数一共有___项;
②若正数x、y、z和正数m、n、p,满足x+m=y+n=z+p=t,请通过构造图形比较px+my+nz与t2的大小(画出图形,并说明理由);
③已知x、y、z满足x+y+z=2m,x2+y2+z2=2n,xyz=p,求x2y2+y2z2+x2z2的值(用含m、n、P的式子表示)
6
从课本出发:1. 完全平方公式:a2±2ab+b2=(a±b)2
2.平方差公式:a2-b2=(a+b)(a-b)
类型一:完全平方公式与图形面积
问题一:通常情况下,用两种不同的方法计算同一图形的面积,可以得到一个恒等式,
①如图1,用4块完全相同的长方形围成一个正方形.根据图中阴影部分的面积可表示为__________,还可表示为___________,可以得到的恒等式是___________.
②类似地,用两种不同的方法计算同一各几何体的体积,也可以得到一个恒等式,如图2是边长为的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
应用:1.如图为某正方形的房屋结构平面图,其中主卧与客卧都为正方形,其面积之和比其余面积(阴影部分)多2.25平方米,则主卧与客卧的周长差为( )
A.12米 B.10米 C.8米 D.6米
2.如图所示,将一张长方形纸板按图中虚线裁剪成九块,若图中①②都是剪成边为a的大正方形,③④都是剪成边长为b的小正方形,⑤⑥⑦⑧⑨都是剪成边长分别为a、b的小长方形﹒
(1)观察图形,可以发现多项式2a2+5ab+2b2可以因式分解为____________________;
(2)若每块小长方形的的面积为3cm2,四个正方形的面积之和为38cm2,试求图中所有裁剪线(虚线部分)长之和﹒
﹒
3.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
类型二: 平方差公式与图形面积
问题二:通常情况下用两种不同的方法计算同一个图形的面积,可以得到一个恒等式。类似地。
(1)如图①,在边长为a的正方形纸片上剪去一个边长为b(b
由此可以验证的乘法公式是___.
(2)类似地,在边长为a的正方体上割去一个边长为b(b
由此可以得到的等式是________________________________,并证明这个等式.
应用:4.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
A. 2cm2 B. 2acm2 C. 4acm2 D. (a2-1)cm2
5.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,求
(1)正方形A,B的面积之和为 ﹒
(2)三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
小结:本节课你学到了什么?
课后作业:
1. 有若干张面积分别为a2、b2、ab的正方形和长方形纸片,阳阳从中抽取了1张面积为a2的正方形纸片,6张面积为ab的长方形纸片,若他想拼成一个大正方形,则还需要抽取面积为b2的正方形纸片( )
A.6张B.7张C.8张D.9张
2.如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为( )
A. a2-4b2 B. (a+b)(a-b) C. (a+2b)(a-b) D. (a+b)(a-2b)
3.如图,点M是AB的中点,点P在MB上。分别以AP,PB为边作正方形APCD和正方形PBEF,连接MD和ME。设AP=a,BP=b,且a+b=10,ab=20,则图中阴影部分的面积为_________________。
4.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,测得的线段长度如图所示,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子.
(1)用含有a,b的代数式表示该长方体盒子的体积,并化简.
(2)若a=12,b=2,求此长方体盒子的体积.
5. 小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=25,ab=12,求小红家这块L形菜地的面积.
6.我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:
就可以用如图所示的面积关系来说明。
(1)请根据如图写出代数恒等式,并根据所写恒等式计算:
(2)若求的值;
(3)现有如图中的彩色卡片:A型、B型、C型,把这些卡片不重叠不留缝隙地贴在棱长为的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用
7.(阅读理解)
“若满足,求的值”
解:设,则,
所以
(解决问题)
(1)若满足,求的值.
(2)若满足,求的值.
(3)如图,正方形的边长为,,长方形的面积是500,四边形和都是正方形,是长方形,求图中阴影部分的面积。
8.一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.
9.如图是一个长为、宽为的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
(1)如图中的阴影部分面积为: ;(用、的代数式表示)
(2)观察如图,请你写出、、之间的等量关系是 ;
(3)根据(2)中的结论,若,,则 ;
(4)实际上通过计算图形的阴影可以探求相应的等式,如图,请你写出这个等式 ;
(5)如图,线段 (其中为正数),点线在段上,在线段同侧作正方形及正方形,连接,,得到.当时,的面积记为;当时,的面积记为;当时,的面积记为;当时,的面积记为,则 .
10.借助图形直观,感受数与形之间的关系,我们常常可以发现一些重要结论.
初步应用 (1)①如图1,大长方形的面积可以看成4个小长方形的面积之和,由此得到多项式乘多项式的运算法,则______(用图中字母表示)
②如图2,借助①,写出一个我们学过的公式:______(用图中字母表示)
深入探究 (2)仿照图2,构造图形并计算(a+b+c)2
拓展延伸 借助以上探究经验,解决下列问题:(3)①代数式(a1+a2+a2+a3+a4+a5)2展开、合并同类项后,得到的多项式的项数一共有___项;
②若正数x、y、z和正数m、n、p,满足x+m=y+n=z+p=t,请通过构造图形比较px+my+nz与t2的大小(画出图形,并说明理由);
③已知x、y、z满足x+y+z=2m,x2+y2+z2=2n,xyz=p,求x2y2+y2z2+x2z2的值(用含m、n、P的式子表示)
6
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
