苏科版七年级数学下册 第9章 数学活动 拼图·公式 教案
文档属性
| 名称 | 苏科版七年级数学下册 第9章 数学活动 拼图·公式 教案 | 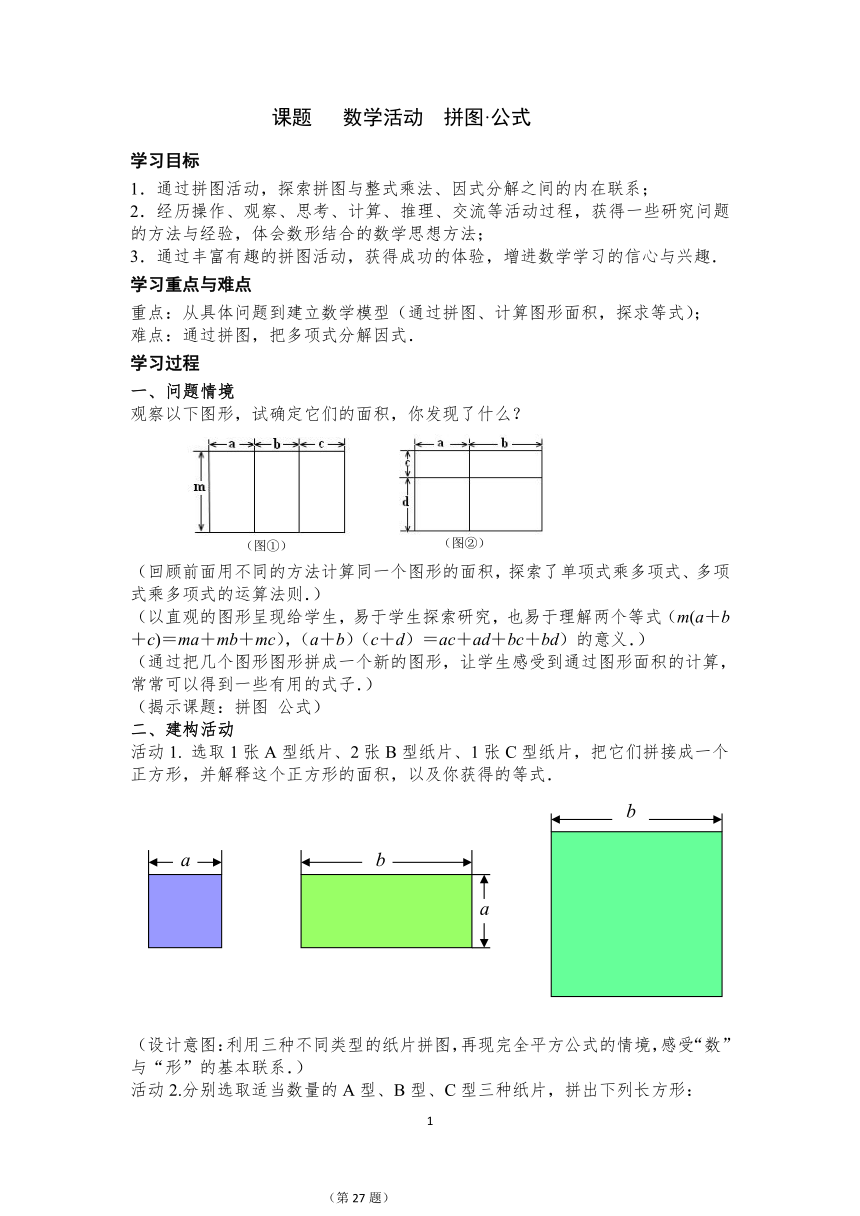 | |
| 格式 | docx | ||
| 文件大小 | 56.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 12:59:45 | ||
图片预览

文档简介
课题 数学活动 拼图·公式
学习目标
1.通过拼图活动,探索拼图与整式乘法、因式分解之间的内在联系;
2.经历操作、观察、思考、计算、推理、交流等活动过程,获得一些研究问题的方法与经验,体会数形结合的数学思想方法;
3.通过丰富有趣的拼图活动,获得成功的体验,增进数学学习的信心与兴趣.
学习重点与难点
重点:从具体问题到建立数学模型(通过拼图、计算图形面积,探求等式);
难点:通过拼图,把多项式分解因式.
学习过程
一、问题情境
观察以下图形,试确定它们的面积,你发现了什么?
(
(第27题)
)
(
(图②)
) (
(图①)
)
(
(第27题)
)
(回顾前面用不同的方法计算同一个图形的面积,探索了单项式乘多项式、多项式乘多项式的运算法则.)
(以直观的图形呈现给学生,易于学生探索研究,也易于理解两个等式(m(a+b+c)=ma+mb+mc),(a+b)(c+d)=ac+ad+bc+bd)的意义.)
(通过把几个图形图形拼成一个新的图形,让学生感受到通过图形面积的计算,常常可以得到一些有用的式子.)
(揭示课题:拼图 公式)
二、建构活动
活动1. 选取1张A型纸片、2张B型纸片、1张C型纸片,把它们拼接成一个正方形,并解释这个正方形的面积,以及你获得的等式.
(
a
b
b
a
)
(设计意图:利用三种不同类型的纸片拼图,再现完全平方公式的情境,感受“数”与“形”的基本联系.)
活动2.分别选取适当数量的A型、B型、C型三种纸片,拼出下列长方形:
(1)边长分别为2a、3b+a的长方形;
(2)边长分别为a+2b、a+b的长方形.
(设计意图:通过已知边长拼长方形活动,在反复尝试的过程中,逐步感受到不同纸片的选择数量与系数之间的关系,初步形成拼图的一般方法,并理解图形与所得等式的联系,完成由“形”到“数”的过程.)
活动3.分别选取适当数量的A型、B型、C型三种纸片,尝试将它们拼成一个长方形,并且使所拼长方形的面积分别为:
(1)3a2+4ab+b2; (2)2a2+5ab+3b2.
(设计意图:通过已知面积拼长方形活动,对由实验观察到的现象进行分析,获得能拼出长方形的规律性的认识,感悟数量关系与图形性质的相互转化.)
三、数学概念(模型)
1.把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式.
2.从面积导出公式也有局限性(字母表示正数),因此还需从代数运算的角度来进一步认识这些等式.
四、应用与拓展
活动4.(1)写一个关于a、b的二次三项式,如a2+4ab+3b2,试用拼一个长方形的方法,把这个二次三项式分解因式.
(设计意图:探索拼图与因式分解之间的内在联系,初步感悟用“十字相乘法”分解因式.)
(2)如果任意写出一个关于a、b的二次多项式,能否用若干块准备好的硬纸片拼成一个长方形,使这个长方形的面积可以用这个式子表示?如不能,你认为具备什么形式的二次多项式可以表示一个长方形的面积?
五、评价小结
从这节课中你有哪些收获?
(数学活动借助于纸片拼图活动,经历操作、探究、解决问题的过程,探索拼图与整式乘法以及因式分解之间的内在联系.先由“形”得到一些关于“数”的结论,然后借助图形反映出部分“数”的几何意义,在动手“做”中向知识的纵深发展,积累有效的基本数学活动经验.)
六、课后作业
1.课本第89页小结与思考4:两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如图9-10.试用不同的方法计算这个图形的面积,你能发现什么?
(
(
图9-10
)
)
2.现有足够的2×2,3×3的正方形和2×3的长方形纸片A、B、C(如图所示),现从中各选取若干个纸片拼成不同的图形,请你在下面给出的方格纸中,按下列要求分别画出一种示意图(说明:下面给出的方格纸中,每个小正方形的边长均为1,拼出的图形,要求每两个图片之间既无缝隙,也无重叠,画图必须保留拼接的痕迹)
(1)选取4张A型纸片,1张B型纸片,4张C型纸片,拼成一个正方形;
(2)选取3张A型纸片,1张B型纸片,若干张C型纸片,拼成一个正方形.
2
学习目标
1.通过拼图活动,探索拼图与整式乘法、因式分解之间的内在联系;
2.经历操作、观察、思考、计算、推理、交流等活动过程,获得一些研究问题的方法与经验,体会数形结合的数学思想方法;
3.通过丰富有趣的拼图活动,获得成功的体验,增进数学学习的信心与兴趣.
学习重点与难点
重点:从具体问题到建立数学模型(通过拼图、计算图形面积,探求等式);
难点:通过拼图,把多项式分解因式.
学习过程
一、问题情境
观察以下图形,试确定它们的面积,你发现了什么?
(
(第27题)
)
(
(图②)
) (
(图①)
)
(
(第27题)
)
(回顾前面用不同的方法计算同一个图形的面积,探索了单项式乘多项式、多项式乘多项式的运算法则.)
(以直观的图形呈现给学生,易于学生探索研究,也易于理解两个等式(m(a+b+c)=ma+mb+mc),(a+b)(c+d)=ac+ad+bc+bd)的意义.)
(通过把几个图形图形拼成一个新的图形,让学生感受到通过图形面积的计算,常常可以得到一些有用的式子.)
(揭示课题:拼图 公式)
二、建构活动
活动1. 选取1张A型纸片、2张B型纸片、1张C型纸片,把它们拼接成一个正方形,并解释这个正方形的面积,以及你获得的等式.
(
a
b
b
a
)
(设计意图:利用三种不同类型的纸片拼图,再现完全平方公式的情境,感受“数”与“形”的基本联系.)
活动2.分别选取适当数量的A型、B型、C型三种纸片,拼出下列长方形:
(1)边长分别为2a、3b+a的长方形;
(2)边长分别为a+2b、a+b的长方形.
(设计意图:通过已知边长拼长方形活动,在反复尝试的过程中,逐步感受到不同纸片的选择数量与系数之间的关系,初步形成拼图的一般方法,并理解图形与所得等式的联系,完成由“形”到“数”的过程.)
活动3.分别选取适当数量的A型、B型、C型三种纸片,尝试将它们拼成一个长方形,并且使所拼长方形的面积分别为:
(1)3a2+4ab+b2; (2)2a2+5ab+3b2.
(设计意图:通过已知面积拼长方形活动,对由实验观察到的现象进行分析,获得能拼出长方形的规律性的认识,感悟数量关系与图形性质的相互转化.)
三、数学概念(模型)
1.把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式.
2.从面积导出公式也有局限性(字母表示正数),因此还需从代数运算的角度来进一步认识这些等式.
四、应用与拓展
活动4.(1)写一个关于a、b的二次三项式,如a2+4ab+3b2,试用拼一个长方形的方法,把这个二次三项式分解因式.
(设计意图:探索拼图与因式分解之间的内在联系,初步感悟用“十字相乘法”分解因式.)
(2)如果任意写出一个关于a、b的二次多项式,能否用若干块准备好的硬纸片拼成一个长方形,使这个长方形的面积可以用这个式子表示?如不能,你认为具备什么形式的二次多项式可以表示一个长方形的面积?
五、评价小结
从这节课中你有哪些收获?
(数学活动借助于纸片拼图活动,经历操作、探究、解决问题的过程,探索拼图与整式乘法以及因式分解之间的内在联系.先由“形”得到一些关于“数”的结论,然后借助图形反映出部分“数”的几何意义,在动手“做”中向知识的纵深发展,积累有效的基本数学活动经验.)
六、课后作业
1.课本第89页小结与思考4:两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如图9-10.试用不同的方法计算这个图形的面积,你能发现什么?
(
(
图9-10
)
)
2.现有足够的2×2,3×3的正方形和2×3的长方形纸片A、B、C(如图所示),现从中各选取若干个纸片拼成不同的图形,请你在下面给出的方格纸中,按下列要求分别画出一种示意图(说明:下面给出的方格纸中,每个小正方形的边长均为1,拼出的图形,要求每两个图片之间既无缝隙,也无重叠,画图必须保留拼接的痕迹)
(1)选取4张A型纸片,1张B型纸片,4张C型纸片,拼成一个正方形;
(2)选取3张A型纸片,1张B型纸片,若干张C型纸片,拼成一个正方形.
2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
