8.3动能和动能定理(Word版含答案)
文档属性
| 名称 | 8.3动能和动能定理(Word版含答案) | 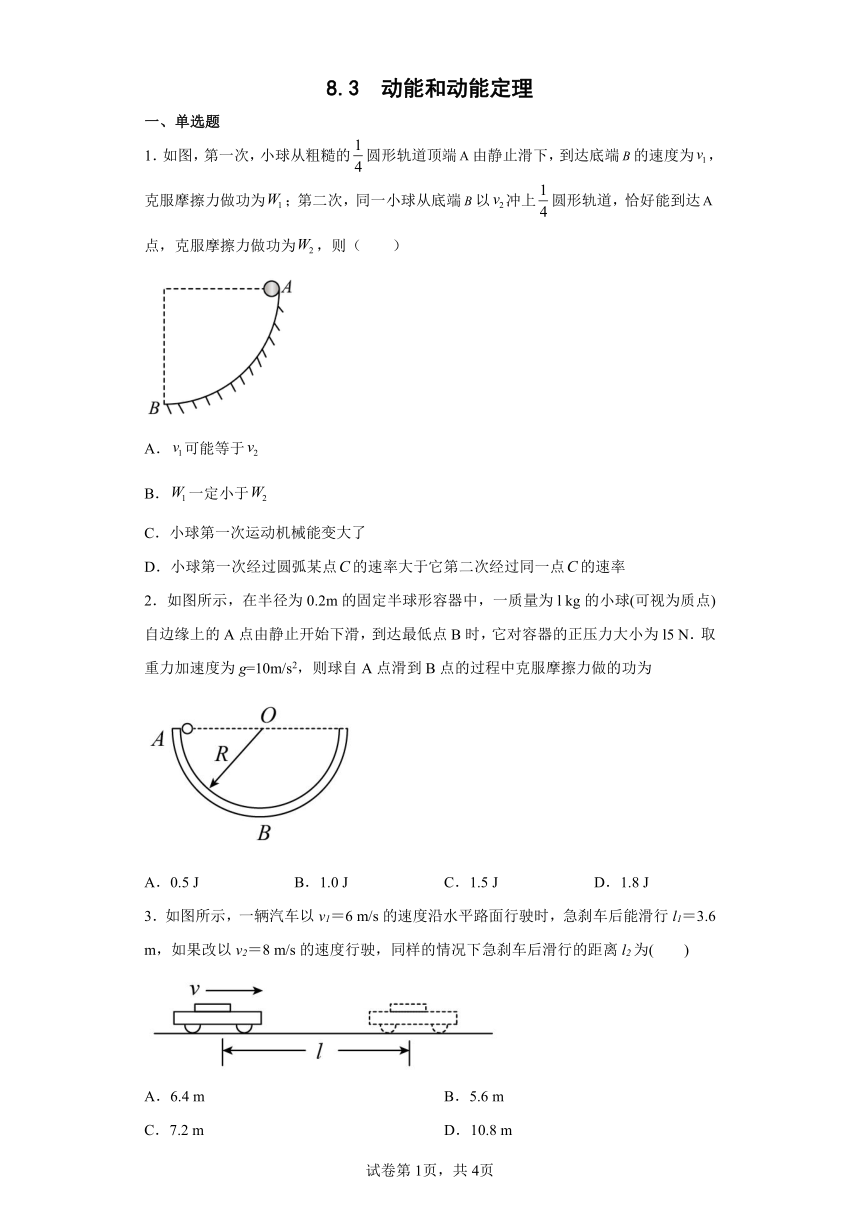 | |
| 格式 | docx | ||
| 文件大小 | 719.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-15 09:26:59 | ||
图片预览





文档简介
8.3 动能和动能定理
一、单选题
1.如图,第一次,小球从粗糙的圆形轨道顶端由静止滑下,到达底端的速度为,克服摩擦力做功为;第二次,同一小球从底端以冲上圆形轨道,恰好能到达点,克服摩擦力做功为,则( )
A.可能等于
B.一定小于
C.小球第一次运动机械能变大了
D.小球第一次经过圆弧某点的速率大于它第二次经过同一点的速率
2.如图所示,在半径为0.2m的固定半球形容器中,一质量为l kg的小球(可视为质点)自边缘上的A点由静止开始下滑,到达最低点B时,它对容器的正压力大小为l5 N.取重力加速度为g=10m/s2,则球自A点滑到B点的过程中克服摩擦力做的功为
A.0.5 J B.1.0 J C.1.5 J D.1.8 J
3.如图所示,一辆汽车以v1=6 m/s的速度沿水平路面行驶时,急刹车后能滑行l1=3.6 m,如果改以v2=8 m/s的速度行驶,同样的情况下急刹车后滑行的距离l2为( )
A.6.4 m B.5.6 m
C.7.2 m D.10.8 m
4.如图所示,汽车通过缆绳将质量为m的货物从A处沿光滑斜面匀速拉至B处,该过程中货物上升的高度为h,到B处时定滑轮右侧缆绳与水平方向间夹角为,左侧缆绳与斜面间夹角为,货物的速度大小为,已知重力加速度为,则( )
A.汽车一直做匀速直线运动
B.此时汽车的速度大小为
C.此过程中缆绳对货物做功的功率逐渐减小
D.此过程中缆绳对货物做的功为
5.某质量为m的电动玩具小车在平直的水泥路上由静止沿直线加速行驶。经过时间t前进的距离为x,且速度达到最大值vm,设这一过程中电动机的功率恒为P,小车受阻力恒为F,则t时间内( )
A.小车做匀加速运动
B.小车受到的牵引力逐渐增大
C.合外力对小车所做的功为Pt
D.牵引力对小车所做的功为Fx+mvm2
6.物体在外力作用下沿光滑水平地面运动,在物体的速度由0增为v的过程中,外力做功W1 , 在物体的速度由v增为2v的过程中,外力做功W2 , 则W1∶W2为
A.1∶1 B.1∶2
C.1∶3 D.1∶4
7.如图所示,水平面的右端与固定的斜面平滑连接于O点,设物块经过O点时无动能损失.物块与水平面及斜面之间的动摩擦因数处处相等,物块从水平面上的M点以某一初速度向右滑动,滑上斜面的最高点为P,P点距O点的水平距离为,竖直距离为,如果其它条件不变,减小斜面的倾角,物块滑到斜面的最高点为Q,Q点距O点的水平距离为,竖直距离为,下列判断正确的是( )
A. B. C. D.
二、多选题
8.如图所示,将质量为m的石块从离地面h高处以初速度v0斜向上抛出,以抛出点所在的水平面为重力势能零平面,不计空气阻力,当石块落地时( )
A.动能为 B.机械能为
C.动能为mgh+ D.重力势能为mgh
9.一代代物理学家在探究客观世界的过程中,创造出了许多科学的思想方法,极大地推动了自然科学的发展,改变了人类的生产和生活方式。下列说法正确的是( )
A.用质点代替有质量的物体,采用了微元法
B.根据速度定义式,当非常小时,就可以表示物体在时刻的瞬时速度,该定义应用了极限思想方法
C.定义加速度,该定义应用了比值法
D.探究匀变速直线运动位移时,采用了理想模型法
10.下列说法正确的是( )
A.由加速度的定义式可知,加速度与速度的变化量成正比,与时间成反比
B.由牛顿第二定律可知,加速度与物体的合外力成正比,与物体的质量成反比
C.匀变速直线运动的加速度为恒量,因此,加速度为恒量的物体一定做匀变速直线运动
D.匀速圆周运动的加速度方向总与速度垂直,因此,加速度方向总与速度垂直的物体一定要做匀速圆周运动
11.将一物体水平抛出并开始计时,只受重力作用,下列说法正确的是( )
A.速度与时间成正比
B.重力的功率与时间成正比
C.动能的增量与时间成正比
D.动量的增量与时间成正比
三、解答题
12.如图某物体以初动能E0从倾角θ=37°的斜面底A点沿斜面上滑,物体与斜面间的摩擦系数μ=0.5,而且mgsinθ>μmgcosθ.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E.已知AB=s,求BC的长度.(sin37°=0.6、cos37°=0.8)
13.用一台额定功率为P0=60kW的起重机,将一质量为m=500kg的工件由地面竖直吊起,不计摩擦等阻力,取g=10m/s2。求:
(1)工件在被吊起的过程中所能达到的最大速度vm?
(2)若使工件以a=2m/s2的加速度从静止开始匀加速向上吊起,则匀加速过程能维持多长时间?
(3)若起重机在始终保持额定功率的情况下从静止开始吊起工件,经过t1=1s工件的速度vt=10m/s,则此时工件离地面的高度h为多少?
14.如图所示,从距地面高h=5m的A点以一定的初速度水平抛出一金属小球,抛出点与落地点的水平距离x=10m,g取10m/s2,小球所受空气阻力忽略不计.
(1) 求小球在空中的运动时间;
(2) 求小球的初速度大小;
(3) 现将一个质量为0.1kg的塑料球从A点以跟金属小球相同的初速度抛出,测得落地时的速度大小为12m/s,求该过程塑料球克服空气阻力所做的功.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
AD.下滑过程重力做正功、摩擦力做负功,根据动能定理有
上滑过程重力、摩擦力做负功,根据动能定理有
由以上两式可知
且物体在同一位置时上滑速度大于下滑速度相同,AD错误;
B.物体在同一位置时上滑速度大于下滑速度相同,故上滑时对轨道的压力较大,那么摩擦力较大,所以上滑过程克服摩擦力做功比下滑时多,即,B正确;
C.小球第一次运动过程中,由于摩擦生热,所以机械能减少,C错误。
故选B。
2.C
【解析】
【分析】
小球在B点竖直方向上受重力和支持力,根据合力提供向心力求出B点的速度,再根据动能定理求出摩擦力所做的功.
【详解】
在B点有.得.A滑到B的过程中运用动能定理得,得,所以球自A点滑到B点的过程中克服摩擦力做的功为1.5J,C正确.
3.A
【解析】
【详解】
汽车在同样的路面上急刹车,所受的阻力大小相同,设为F,汽车的末速度都为零,根据动能定理有
-Fs1=0-mv12-Fs2=0-mv22
所以,
s2=()2×s1=()2×3.6 m=6.4 m
故选A。
4.B
【解析】
【分析】
【详解】
B.由于缆绳不可伸长,汽车沿绳的分速度等于货物沿绳的分速度,当货物上升到B处时满足
故此时汽车的速度大小为
B正确;
A.设右侧绳与水平方向夹角,左侧绳与斜面夹角,类比B的解析可得汽车的速度大小为
由于减小,增大,则车速减小,故汽车做减速运动,A错误;
C.设斜面倾角,对货物在沿斜面方向满足
此过程中缆绳对货物做功的功率为
保持不变,C错误;
D.此过程中对货物由动能定理可得
则缆绳对货物做的功为
D错误。
故选B。
5.D
【解析】
【分析】
【详解】
AB.电动机功率恒定
P=F牵v
结合牛顿第二定律可知
F牵-F=ma
v=at
可知,当速度增大时,牵引力减小,加速度减小,故小车做加速度减小的变加速运动,故AB错误;
C.整个过程中,牵引力做正功,阻力做负功,故合力做功为
W=mvm2
Pt为牵引力所做的功,故C错误;
D.整个过程中,根据动能定理可知
Pt Fx=mvm2
解得
Pt=Fx+mvm2
故D正确。
故选D。
6.C
【解析】
【详解】
由动能定理可得, ,
所以W1:W2=1:3.故ABD错误,C正确
故选:C
7.D
【解析】
【详解】
设物块经过O点的速度为v,任一斜面的倾角为α,在斜面上上升的竖直高度为h,水平距离为x,根据动能定理得
则得
v相同,α越大时,越大,则得h越大,则有
水平距离
知α越大时,越大,则得x越小,则有
故D正确,ABC错误。
故选D。
【名师点睛】
解决本题的关键要抓住隐含的不变条件:物块经过O点的速度不变,涉及力在空间效果时要优先考虑动能定理,当然也可以用牛顿第二定律与运动公式结合使用,但是运算较复杂,同学可经过做题尝试一下两种方法。
8.BC
【解析】
【详解】
AC.从抛出点到落地过程中由动能定理得
则
故A错误,C正确;
B.石块在抛出点的机械能为,由于抛出后只有重力做功则其机械能守恒,所以落地时的机械能也为,故B正确;
D.以抛出点所在的水平面为重力势能零平面,则落地时的重力势能为,故D错误。
故选BC。
9.BC
【解析】
【分析】
【详解】
A.在不考虑物体的大小和形状时,用质点来代替物体的方法是理想化物理模型法,A错误;
B.为研究某一时刻或某一位置时的速度,我们采用了取时间非常小,即让时间趋向无穷小时的平均速度作用瞬时速度,即采用了极限思维法,B正确;
C.定义加速度时
该定义应用了比值法,C正确;
D.探究匀变速直线运动位移
时,采用了等效替代法,D错误。
故选BC。
10.BD
【解析】
【详解】
由加速度的定义式可知,当时间一定时,加速度与速度的变化量成正比,故A错误;由牛顿第二定律a=F/m可知,加速度与物体的合外力成正比,与物体的质量成反比,故B正确;加速度为恒量的物体不一定做匀变速直线运动,如平抛运动,故C错误;加速度方向总与速度垂直的物体一定做匀速圆周运动,故D正确.故选BD.
11.BD
【解析】
【分析】
【详解】
A.根据平抛运动的两分运动规律有
可知瞬时速度与时间不成正比。故A错误;
B.根据瞬时功率的定义,有
则瞬时功率与时间成正比。故B正确;
C.根据动能定理有
故动能的增量与时间不成正比。故C错误;
D.由动量定理可知
则动量的变化量与时间成正比。故D正确。
故选BD。
12.
【解析】
【详解】
设BC=s1;物体从B点滑到C点再从C点滑到D点的过程中EKB=EKD,即动能的增量为0.在这过程中,重力所做的功与路径无关,它等于mgsinθ s/2
摩擦力所做的功为-μmgcosθ(s/2+ 2s1)
由动能定理W合=△EK,得到:mgsinθ s/2-μmgcosθ(s/2+ 2s1)=0,
s1=(sinθ-μcosθ)s/4μcosθ=s/8
13.(1)12m/s;(2)5s;(3)7m
【解析】
【详解】
(1)当工件达到最大速度时,加速度为0
功率达到额定功率
故
(2)工件被匀加速向上吊起时,a不变,v变大,P也变大,当P=P0时匀加速过程结束,根据牛顿第二定律得
解得
匀加速过程结束时工件的速度为
匀加速过程持续的时间为
(3)根据动能定理,有
代入数据解得
14.(1) (2) (3)
【解析】
【详解】
(1)由 得:小球在空中的运动时间: ;
(2)小球的初速度大小 ;
(3)由动能定理得:
解得:
即这个过程克服空气阻力做功为2.8J
故本题答案是:(1) (2) (3)
点睛:平抛运动可以分解为水平方向上的匀速运动与竖直方向上的自由落体运动,并会利用动能定理求解空气阻力做的功.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,第一次,小球从粗糙的圆形轨道顶端由静止滑下,到达底端的速度为,克服摩擦力做功为;第二次,同一小球从底端以冲上圆形轨道,恰好能到达点,克服摩擦力做功为,则( )
A.可能等于
B.一定小于
C.小球第一次运动机械能变大了
D.小球第一次经过圆弧某点的速率大于它第二次经过同一点的速率
2.如图所示,在半径为0.2m的固定半球形容器中,一质量为l kg的小球(可视为质点)自边缘上的A点由静止开始下滑,到达最低点B时,它对容器的正压力大小为l5 N.取重力加速度为g=10m/s2,则球自A点滑到B点的过程中克服摩擦力做的功为
A.0.5 J B.1.0 J C.1.5 J D.1.8 J
3.如图所示,一辆汽车以v1=6 m/s的速度沿水平路面行驶时,急刹车后能滑行l1=3.6 m,如果改以v2=8 m/s的速度行驶,同样的情况下急刹车后滑行的距离l2为( )
A.6.4 m B.5.6 m
C.7.2 m D.10.8 m
4.如图所示,汽车通过缆绳将质量为m的货物从A处沿光滑斜面匀速拉至B处,该过程中货物上升的高度为h,到B处时定滑轮右侧缆绳与水平方向间夹角为,左侧缆绳与斜面间夹角为,货物的速度大小为,已知重力加速度为,则( )
A.汽车一直做匀速直线运动
B.此时汽车的速度大小为
C.此过程中缆绳对货物做功的功率逐渐减小
D.此过程中缆绳对货物做的功为
5.某质量为m的电动玩具小车在平直的水泥路上由静止沿直线加速行驶。经过时间t前进的距离为x,且速度达到最大值vm,设这一过程中电动机的功率恒为P,小车受阻力恒为F,则t时间内( )
A.小车做匀加速运动
B.小车受到的牵引力逐渐增大
C.合外力对小车所做的功为Pt
D.牵引力对小车所做的功为Fx+mvm2
6.物体在外力作用下沿光滑水平地面运动,在物体的速度由0增为v的过程中,外力做功W1 , 在物体的速度由v增为2v的过程中,外力做功W2 , 则W1∶W2为
A.1∶1 B.1∶2
C.1∶3 D.1∶4
7.如图所示,水平面的右端与固定的斜面平滑连接于O点,设物块经过O点时无动能损失.物块与水平面及斜面之间的动摩擦因数处处相等,物块从水平面上的M点以某一初速度向右滑动,滑上斜面的最高点为P,P点距O点的水平距离为,竖直距离为,如果其它条件不变,减小斜面的倾角,物块滑到斜面的最高点为Q,Q点距O点的水平距离为,竖直距离为,下列判断正确的是( )
A. B. C. D.
二、多选题
8.如图所示,将质量为m的石块从离地面h高处以初速度v0斜向上抛出,以抛出点所在的水平面为重力势能零平面,不计空气阻力,当石块落地时( )
A.动能为 B.机械能为
C.动能为mgh+ D.重力势能为mgh
9.一代代物理学家在探究客观世界的过程中,创造出了许多科学的思想方法,极大地推动了自然科学的发展,改变了人类的生产和生活方式。下列说法正确的是( )
A.用质点代替有质量的物体,采用了微元法
B.根据速度定义式,当非常小时,就可以表示物体在时刻的瞬时速度,该定义应用了极限思想方法
C.定义加速度,该定义应用了比值法
D.探究匀变速直线运动位移时,采用了理想模型法
10.下列说法正确的是( )
A.由加速度的定义式可知,加速度与速度的变化量成正比,与时间成反比
B.由牛顿第二定律可知,加速度与物体的合外力成正比,与物体的质量成反比
C.匀变速直线运动的加速度为恒量,因此,加速度为恒量的物体一定做匀变速直线运动
D.匀速圆周运动的加速度方向总与速度垂直,因此,加速度方向总与速度垂直的物体一定要做匀速圆周运动
11.将一物体水平抛出并开始计时,只受重力作用,下列说法正确的是( )
A.速度与时间成正比
B.重力的功率与时间成正比
C.动能的增量与时间成正比
D.动量的增量与时间成正比
三、解答题
12.如图某物体以初动能E0从倾角θ=37°的斜面底A点沿斜面上滑,物体与斜面间的摩擦系数μ=0.5,而且mgsinθ>μmgcosθ.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E.已知AB=s,求BC的长度.(sin37°=0.6、cos37°=0.8)
13.用一台额定功率为P0=60kW的起重机,将一质量为m=500kg的工件由地面竖直吊起,不计摩擦等阻力,取g=10m/s2。求:
(1)工件在被吊起的过程中所能达到的最大速度vm?
(2)若使工件以a=2m/s2的加速度从静止开始匀加速向上吊起,则匀加速过程能维持多长时间?
(3)若起重机在始终保持额定功率的情况下从静止开始吊起工件,经过t1=1s工件的速度vt=10m/s,则此时工件离地面的高度h为多少?
14.如图所示,从距地面高h=5m的A点以一定的初速度水平抛出一金属小球,抛出点与落地点的水平距离x=10m,g取10m/s2,小球所受空气阻力忽略不计.
(1) 求小球在空中的运动时间;
(2) 求小球的初速度大小;
(3) 现将一个质量为0.1kg的塑料球从A点以跟金属小球相同的初速度抛出,测得落地时的速度大小为12m/s,求该过程塑料球克服空气阻力所做的功.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
AD.下滑过程重力做正功、摩擦力做负功,根据动能定理有
上滑过程重力、摩擦力做负功,根据动能定理有
由以上两式可知
且物体在同一位置时上滑速度大于下滑速度相同,AD错误;
B.物体在同一位置时上滑速度大于下滑速度相同,故上滑时对轨道的压力较大,那么摩擦力较大,所以上滑过程克服摩擦力做功比下滑时多,即,B正确;
C.小球第一次运动过程中,由于摩擦生热,所以机械能减少,C错误。
故选B。
2.C
【解析】
【分析】
小球在B点竖直方向上受重力和支持力,根据合力提供向心力求出B点的速度,再根据动能定理求出摩擦力所做的功.
【详解】
在B点有.得.A滑到B的过程中运用动能定理得,得,所以球自A点滑到B点的过程中克服摩擦力做的功为1.5J,C正确.
3.A
【解析】
【详解】
汽车在同样的路面上急刹车,所受的阻力大小相同,设为F,汽车的末速度都为零,根据动能定理有
-Fs1=0-mv12-Fs2=0-mv22
所以,
s2=()2×s1=()2×3.6 m=6.4 m
故选A。
4.B
【解析】
【分析】
【详解】
B.由于缆绳不可伸长,汽车沿绳的分速度等于货物沿绳的分速度,当货物上升到B处时满足
故此时汽车的速度大小为
B正确;
A.设右侧绳与水平方向夹角,左侧绳与斜面夹角,类比B的解析可得汽车的速度大小为
由于减小,增大,则车速减小,故汽车做减速运动,A错误;
C.设斜面倾角,对货物在沿斜面方向满足
此过程中缆绳对货物做功的功率为
保持不变,C错误;
D.此过程中对货物由动能定理可得
则缆绳对货物做的功为
D错误。
故选B。
5.D
【解析】
【分析】
【详解】
AB.电动机功率恒定
P=F牵v
结合牛顿第二定律可知
F牵-F=ma
v=at
可知,当速度增大时,牵引力减小,加速度减小,故小车做加速度减小的变加速运动,故AB错误;
C.整个过程中,牵引力做正功,阻力做负功,故合力做功为
W=mvm2
Pt为牵引力所做的功,故C错误;
D.整个过程中,根据动能定理可知
Pt Fx=mvm2
解得
Pt=Fx+mvm2
故D正确。
故选D。
6.C
【解析】
【详解】
由动能定理可得, ,
所以W1:W2=1:3.故ABD错误,C正确
故选:C
7.D
【解析】
【详解】
设物块经过O点的速度为v,任一斜面的倾角为α,在斜面上上升的竖直高度为h,水平距离为x,根据动能定理得
则得
v相同,α越大时,越大,则得h越大,则有
水平距离
知α越大时,越大,则得x越小,则有
故D正确,ABC错误。
故选D。
【名师点睛】
解决本题的关键要抓住隐含的不变条件:物块经过O点的速度不变,涉及力在空间效果时要优先考虑动能定理,当然也可以用牛顿第二定律与运动公式结合使用,但是运算较复杂,同学可经过做题尝试一下两种方法。
8.BC
【解析】
【详解】
AC.从抛出点到落地过程中由动能定理得
则
故A错误,C正确;
B.石块在抛出点的机械能为,由于抛出后只有重力做功则其机械能守恒,所以落地时的机械能也为,故B正确;
D.以抛出点所在的水平面为重力势能零平面,则落地时的重力势能为,故D错误。
故选BC。
9.BC
【解析】
【分析】
【详解】
A.在不考虑物体的大小和形状时,用质点来代替物体的方法是理想化物理模型法,A错误;
B.为研究某一时刻或某一位置时的速度,我们采用了取时间非常小,即让时间趋向无穷小时的平均速度作用瞬时速度,即采用了极限思维法,B正确;
C.定义加速度时
该定义应用了比值法,C正确;
D.探究匀变速直线运动位移
时,采用了等效替代法,D错误。
故选BC。
10.BD
【解析】
【详解】
由加速度的定义式可知,当时间一定时,加速度与速度的变化量成正比,故A错误;由牛顿第二定律a=F/m可知,加速度与物体的合外力成正比,与物体的质量成反比,故B正确;加速度为恒量的物体不一定做匀变速直线运动,如平抛运动,故C错误;加速度方向总与速度垂直的物体一定做匀速圆周运动,故D正确.故选BD.
11.BD
【解析】
【分析】
【详解】
A.根据平抛运动的两分运动规律有
可知瞬时速度与时间不成正比。故A错误;
B.根据瞬时功率的定义,有
则瞬时功率与时间成正比。故B正确;
C.根据动能定理有
故动能的增量与时间不成正比。故C错误;
D.由动量定理可知
则动量的变化量与时间成正比。故D正确。
故选BD。
12.
【解析】
【详解】
设BC=s1;物体从B点滑到C点再从C点滑到D点的过程中EKB=EKD,即动能的增量为0.在这过程中,重力所做的功与路径无关,它等于mgsinθ s/2
摩擦力所做的功为-μmgcosθ(s/2+ 2s1)
由动能定理W合=△EK,得到:mgsinθ s/2-μmgcosθ(s/2+ 2s1)=0,
s1=(sinθ-μcosθ)s/4μcosθ=s/8
13.(1)12m/s;(2)5s;(3)7m
【解析】
【详解】
(1)当工件达到最大速度时,加速度为0
功率达到额定功率
故
(2)工件被匀加速向上吊起时,a不变,v变大,P也变大,当P=P0时匀加速过程结束,根据牛顿第二定律得
解得
匀加速过程结束时工件的速度为
匀加速过程持续的时间为
(3)根据动能定理,有
代入数据解得
14.(1) (2) (3)
【解析】
【详解】
(1)由 得:小球在空中的运动时间: ;
(2)小球的初速度大小 ;
(3)由动能定理得:
解得:
即这个过程克服空气阻力做功为2.8J
故本题答案是:(1) (2) (3)
点睛:平抛运动可以分解为水平方向上的匀速运动与竖直方向上的自由落体运动,并会利用动能定理求解空气阻力做的功.
答案第1页,共2页
答案第1页,共2页
