27.2.3相似三角形的周长与面积
文档属性
| 名称 | 27.2.3相似三角形的周长与面积 |  | |
| 格式 | zip | ||
| 文件大小 | 345.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-28 13:40:40 | ||
图片预览





文档简介
课件22张PPT。
27.2.3相似三角形的周长与面积探究新知:如果两个三角形相似,它们的周长之间有什么关系?
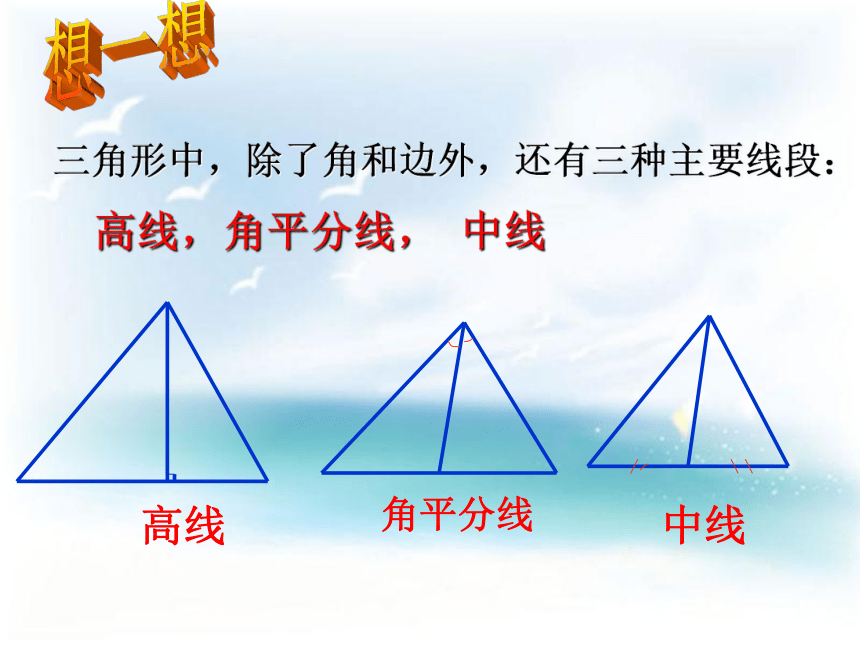
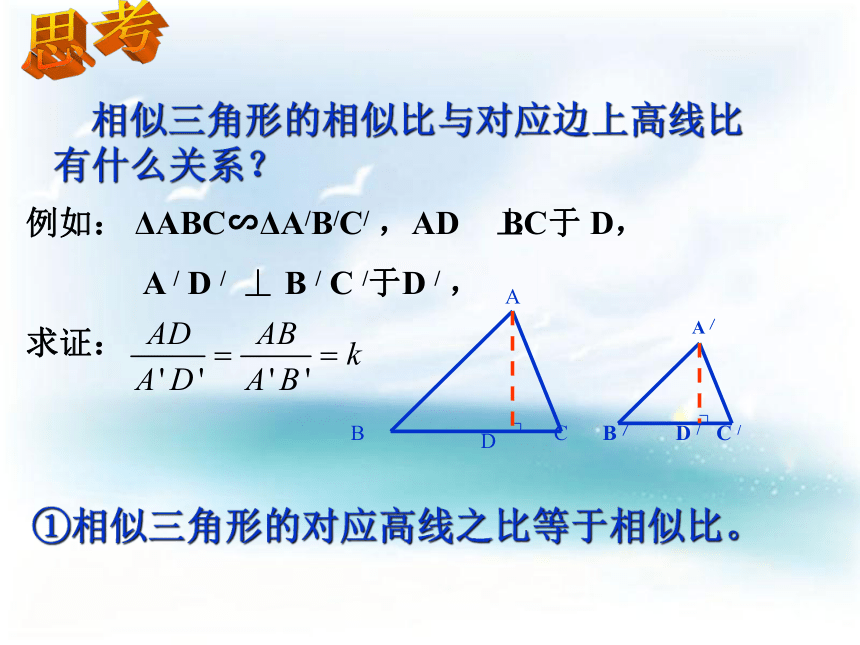
两个相似多边形呢?相似三角形周长的比等于相似比。想一想三角形中,除了角和边外,还有三种主要线段:高线,角平分线, 中线思考 相似三角形的相似比与对应边上高线比有什么关系?例如: ΔABC∽ΔA/B/C/ ,AD BC于 D,
A / D / B / C /于D / ,
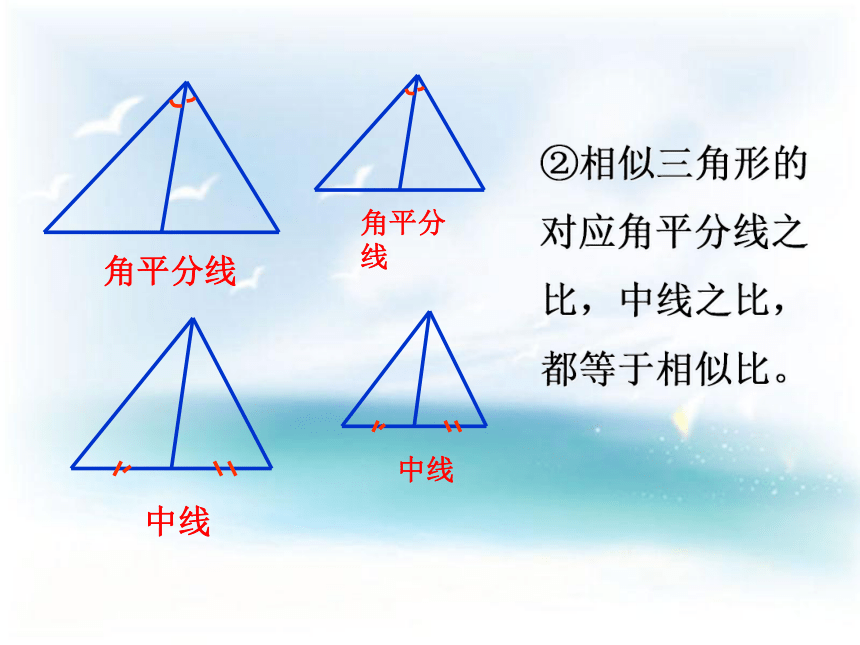
求证: ①相似三角形的对应高线之比等于相似比。②相似三角形的
对应角平分线之
比,中线之比,
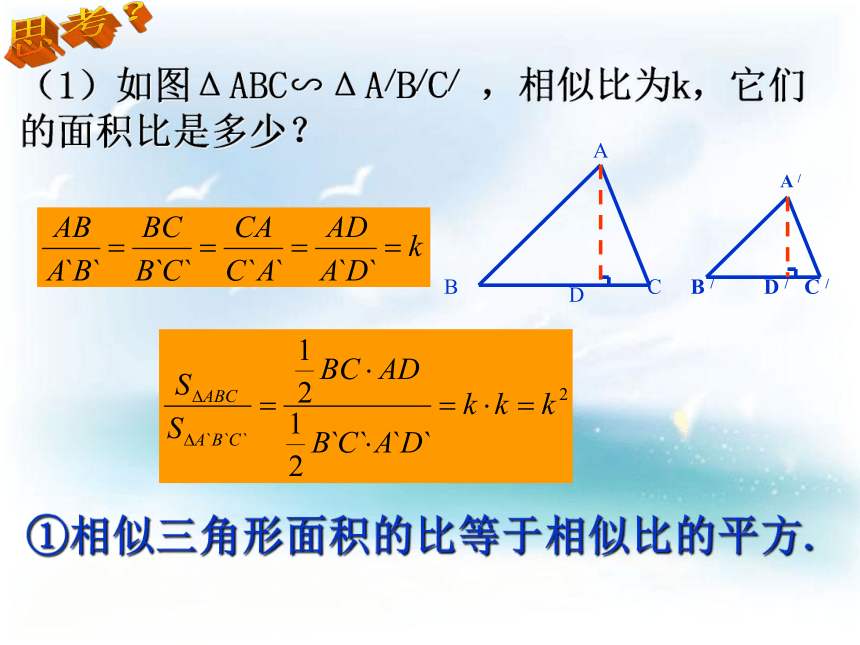
都等于相似比。(1)如图ΔABC∽ΔA/B/C/ ,相似比为k,它们的面积比是多少?思考?①相似三角形面积的比等于相似比的平方. (1)相似三角形对应的 比等于 相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线(2)如图,四边ABCD相似于四边形A/B/C/ D /,相似比为k,①它们周长比是多少?②相似多边形面积的比是多少?相似多边形周长的比等于相似比。相似多边形面积的比等于相似比的平方。尝试应用:
(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3判断题:(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。(√)(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。(×)例1、如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF的周长和面积。解:在△ABC和△DEF中,∵AB=2DE,AC=2DF,
∴又∠D=∠A,
∴△DEF∽△ABC,相似比为∴△DEF的周长为×24=12面积为例 题 讲 解例21、如图,平行四边形ABCD中,AE:EB=1:2,
求△AEF与△CDF周长的比。
如果S△AEF=6 cm2,求S△CDF?练习:2.△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,(1)求△ABC的面积。(2)求四边形BDEF的面积?3.如图,△ABC∽△A'B'C',他们的周长分别为60cm和72cm,且AB=15cm,B'C'=24cm,求BC、AC、A'B'、A'C'的长.解: ∵△ABC∽△A′B′C′ 如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴巩固提高:变式练习 已知:如图,矩形DEFG内接于△ABC,D,E在BC上,F,G分别在AC,AB上,且DE=2EF,BC=21mm,△ABC的高AH=14mm.求矩形的面积.(1)将“正方形”推广到一般情况的“矩形”.S 如图(a),(b),两个全等的等腰直角三角形中,各有一个内接正方形.如果图(a)中正方形的面积是81,求图(b)中正方形的面积.提示:先求出等腰直角三角形直角边长为18,再利用图(b)中的相似解得图(b)中所求正方形的面积为72.(2)将锐角三角形△ABC变为特殊的等腰三角形.如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为4:5,那么该怎么切割呢?DE你会解决引入中的问题了吗?3.在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,求(1)三角形AB边上的高线CH;
(2)设DN=x,NF=y,求y关于x的函数解析式;
(3)当x为何值时,水池DEFN的面积最大,最大为多少?
四 课堂小结 (1)相似三角形对应的 比等于 相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线
27.2.3相似三角形的周长与面积探究新知:如果两个三角形相似,它们的周长之间有什么关系?
两个相似多边形呢?相似三角形周长的比等于相似比。想一想三角形中,除了角和边外,还有三种主要线段:高线,角平分线, 中线思考 相似三角形的相似比与对应边上高线比有什么关系?例如: ΔABC∽ΔA/B/C/ ,AD BC于 D,
A / D / B / C /于D / ,
求证: ①相似三角形的对应高线之比等于相似比。②相似三角形的
对应角平分线之
比,中线之比,
都等于相似比。(1)如图ΔABC∽ΔA/B/C/ ,相似比为k,它们的面积比是多少?思考?①相似三角形面积的比等于相似比的平方. (1)相似三角形对应的 比等于 相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线(2)如图,四边ABCD相似于四边形A/B/C/ D /,相似比为k,①它们周长比是多少?②相似多边形面积的比是多少?相似多边形周长的比等于相似比。相似多边形面积的比等于相似比的平方。尝试应用:
(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3判断题:(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。(√)(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。(×)例1、如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF的周长和面积。解:在△ABC和△DEF中,∵AB=2DE,AC=2DF,
∴又∠D=∠A,
∴△DEF∽△ABC,相似比为∴△DEF的周长为×24=12面积为例 题 讲 解例21、如图,平行四边形ABCD中,AE:EB=1:2,
求△AEF与△CDF周长的比。
如果S△AEF=6 cm2,求S△CDF?练习:2.△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,(1)求△ABC的面积。(2)求四边形BDEF的面积?3.如图,△ABC∽△A'B'C',他们的周长分别为60cm和72cm,且AB=15cm,B'C'=24cm,求BC、AC、A'B'、A'C'的长.解: ∵△ABC∽△A′B′C′ 如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴巩固提高:变式练习 已知:如图,矩形DEFG内接于△ABC,D,E在BC上,F,G分别在AC,AB上,且DE=2EF,BC=21mm,△ABC的高AH=14mm.求矩形的面积.(1)将“正方形”推广到一般情况的“矩形”.S 如图(a),(b),两个全等的等腰直角三角形中,各有一个内接正方形.如果图(a)中正方形的面积是81,求图(b)中正方形的面积.提示:先求出等腰直角三角形直角边长为18,再利用图(b)中的相似解得图(b)中所求正方形的面积为72.(2)将锐角三角形△ABC变为特殊的等腰三角形.如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为4:5,那么该怎么切割呢?DE你会解决引入中的问题了吗?3.在直径为AB的半圆内,划出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,现要建造一个内接于三角形ABC的矩形水池DEFN,其中DE在AB上,如图设计方案是使AC=8,BC=6,求(1)三角形AB边上的高线CH;
(2)设DN=x,NF=y,求y关于x的函数解析式;
(3)当x为何值时,水池DEFN的面积最大,最大为多少?
四 课堂小结 (1)相似三角形对应的 比等于 相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线
