8.1一元二次方程 课件(共31张PPT)
文档属性
| 名称 | 8.1一元二次方程 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
第八章
一元二次方程
8.1一元二次方程
鲁教版数学八年级下册
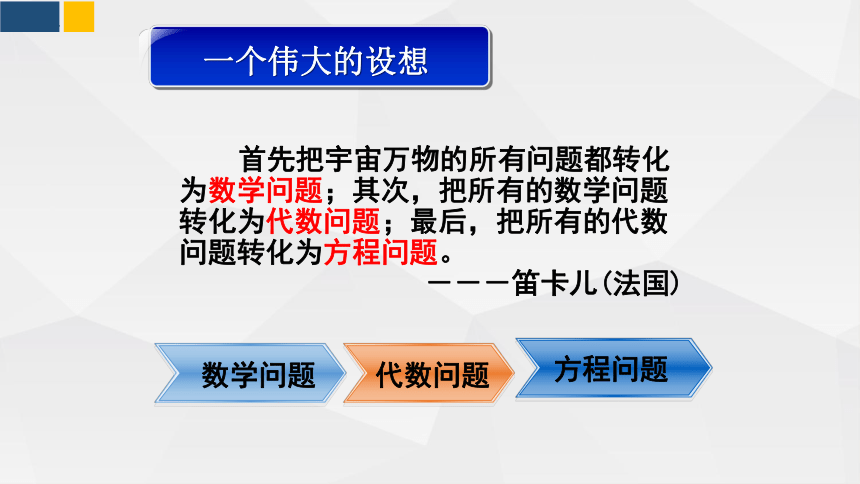
一个伟大的设想
数学问题
代数问题
方程问题
首先把宇宙万物的所有问题都转化为数学问题;其次,把所有的数学问题转化为代数问题;最后,把所有的代数问题转化为方程问题。
---笛卡儿(法国)
2x+3=0
2x+3y=6
FAMILY
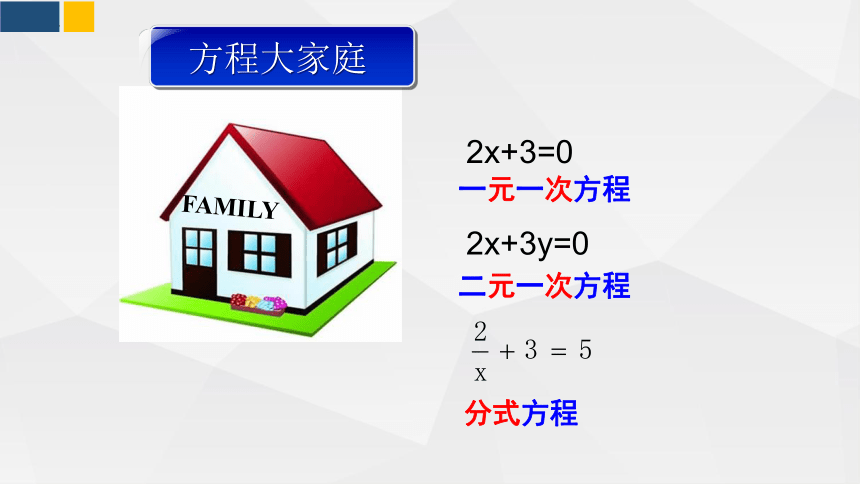
方程大家庭
2x+3=0
2x+3y=0
一元一次方程
二元一次方程
分式方程
2x+3=0
2x+3y=6
FAMILY
方程大家庭
2x+3=0
2x+3y=0
一元一次方程
二元一次方程
分式方程
2x+3=0
2x+3y=6
FAMILY
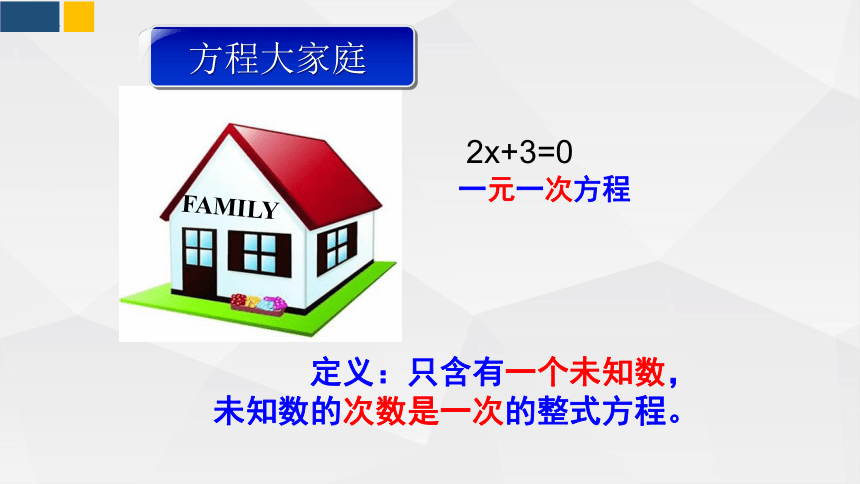
方程大家庭
2x+3=0
一元一次方程
定义:只含有一个未知数,
未知数的次数是一次的整式方程。
探究新知
分享快乐
走近生活
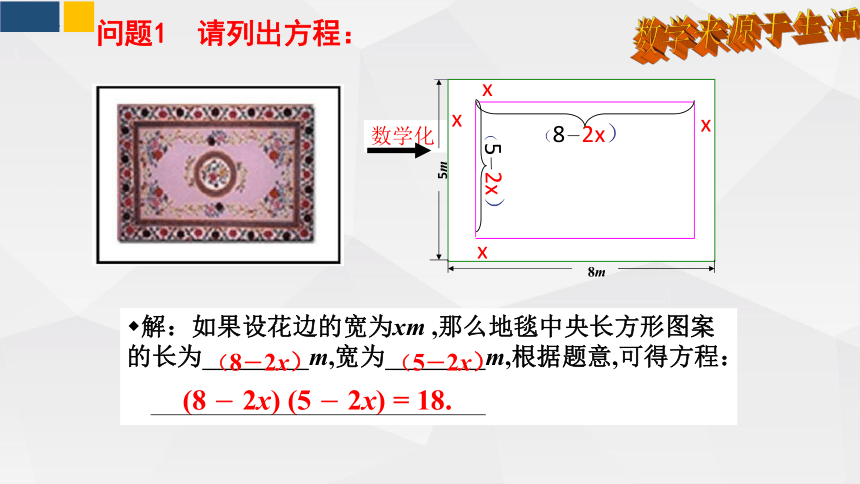
问题情景(1)问题情景(1)
问题1 请列出方程:
数学来源于生活
数学化
问题情景(1)问题情景(1)
解:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m,宽为 m,根据题意,可得方程:
(8-2x)
(5-2x)
(8 - 2x) (5 - 2x) = 18.
5m
8m
(8-2x)
(5-2x)
x
x
x
x
问题1 请列出方程:
数学来源于生活
观察下面等式:
102+112+122=132+142
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为: , , _______, .
x+1
x +2
x +3
x +4
根据题意,可得方程:
.
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
问题情景(2)问题情景(2)
问题2 请列出方程:
数学来源于生活
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
由勾股定理可知,滑动前梯子底端距墙 ____m .
如果设梯子底端滑动X m,那么滑动后梯子底端距墙
m;
根据题意,可得方程:
X+6
72+(X+6)2=102
xm
8m
10m
7m
6m
数学化
1m
问题情景(3)问题情景(3)
6
6m
问题3 请列出方程:
数学来源于生活
你能化简这三个方程吗?方程 ①②③有何特点
x2-12x-15=0
① (8-2x)(5-2x)=18
一元一次方程定义:只含有一个未知数,未知数的次数是一次的整式方程。
一元二次方程
(1)方程两边都是整式
(2)只含有一个未知数
(3)未知数的最高次数是2次
②x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
x2 - 8x-20=0.
2X2-13x+11=0
③72+(X+6)2=102
(4)都可以化成ax2+bx+c=0(a≠0)的形式
一元二次方程
(1)方程两边都是整式
(2)只含有一个未知数
(3)未知数的最高次数是2次
方程 ①②③有何特点
③72+(X+6)2=102 x2-12x-15=0
① (8-2x)(5-2x)=18 2X2-13x+11=0
像这样,只含有一个未知数的整式方程,且都可化成ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做 一元二次方程.
②x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
x2 - 8x-20=0.
(4)都可以化成ax2+bx+c=0(a≠0)的形式
(a≠0,a,b,c为常数)
ax2+ bx +c =0
二次项:ax2 一次项:bx 常数项:c
一元二次方程的一般形式
二次项系数
a
一次项系数
b
常数项
c
(a≠0,a,b,c为常数)
ax2+ bx +c =0
二次项:ax2 一次项:bx 常数项:c
一元二次方程的一般形式
二次项系数
a
一次项系数
b
常数项
c
想一想
为什么要限制a≠0
1.当b=0时
a≠0
2.当c=0时
3.当b=0,c=0时
一元二次方程的特殊形式
ax2+c=0
ax2+bx=0
ax2=0
b、c可以为零吗?
例1:下列方程是一元二次方程的是:
应用新知
(4)
(3)
(2)
(1)
判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②x2= x2- 4x ( )
③ 2xy-7=0 ( ) ④ ( )
1
x2
-
2
x
=0
⑤ ax2 + bx +c=0( )
慧眼找对错
自己编一个一元二次方程
例2:把下列方程化成一般形式,并指出二次项系数,一次项系数和常数项.
一般形式:ax +bx+c=0(a≠0)
应用新知
方程 一般形式 二次项系数 一次项系数 常数项
X2-4x-3=0
(x+1)2= (2x)2
X2-4x-3=0
1
- 4
-3
0.5
0
3x2-2x-1=0
3
-2
-1
-4
-3
抢答
注意
1、整理后书写一元二次方程时,通常降幂排列。
一般情况下,二次项系数应化为正数。
2、系数前面的符号不能丢。
已知关于x的方程(k2-1)x2 +2(k-1)x+3=0
(2)请你写出一个K的值,使原方程为一元一次方程这样的K值唯一吗?
(1)请你写出一个k的值,使原方程为一元二次方程,这样的K值有多少个?
K可以取任意实数吗?若不是,K要受到什么条件的限制?
比一比,哪个小组合作最佳?
k2-1≠0 即K≠±1
即K=-1
k2-1=0
K-1≠0
例3:关于x的方程 (a-2)x|a| -bx+3=0,
a,b为何值,此方程为一元二次方程
拓展延伸
解:(1) a-2≠0
|a|=2
∴a=-2,b是任意实数时是一元二次方程;
a≠2
a=± 2
新知
注意
困惑
感悟
预测方向
体会分享
1.一元二次方程的概念
2.一元二次方程的一般形式
(a≠0,a,b,c为常数)
数学问题
转化
实际问题
方程思想的应用
体会分享
4.两种思想:
类比
一元二次方程
①方程两边都是整式②只含有一个未知数
③未知数的最高次数是2次
3.根据定义确定字母系数的值
一元一次方程
1.请问下列方程哪些是一元二次方程 若是,指出各项的系数
(1)2x2-5xy+6y=0
(4)x2+2x-3=1+x2
你认识一元二次方程了吗?
( )
( )
( )
( )
(3) =0
(2)2x2- -1 =0
课堂 达标检测
2、你能找到五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
解:设五个连续整数中第一个数为x,
则后面四个数依次为_____、_____
_____、______。
根据题意可得方程为:
—————————————————————
X+1
X+2
X+3
X+4
(X+1)2
(X+2)2
+
(X+3)2
(X+4)2
=
+
X2
+
课堂达标检测
3.把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:
方 程 一般形式 二次项 系 数 一次项 系 数 常数项
3x2=5x-1
(x+2)(x -2)=6
4x-x2=0
课堂达标检测
3x2-5x+1=0
x2-10=0
x2-4x=0
3
1
1
-5
0
-4
1
-10
0
4、选做:
关于x的方程(m-2)x|m|+3mx+1=0是
一元二次方程,则 m= .
课堂达标检测
-2
(x-4)2+ (x-2)2= x2
5.从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门框的对角线拿进去。这个醉汉一试,刚好进去.你知道竹竿有多长吗 请根据这一问题列出方程.
即 x2-12 x +20 = 0
解:设竹竿的长为x尺,则门的宽 度为 尺,长为 尺,依题意得方程:
(x-4)
(x-2)
课堂达标检测
必做题:配套练习册P60-62
选做题:5
作业目的:1、进一步巩固一元二次方程的定义及一般形式。2、一元二次方程的实际应用。
作业要求:独立用心完成,保证准确率。
作业布置
给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
---- 高斯
美言分享
谢谢聆听
第八章
一元二次方程
8.1一元二次方程
鲁教版数学八年级下册
一个伟大的设想
数学问题
代数问题
方程问题
首先把宇宙万物的所有问题都转化为数学问题;其次,把所有的数学问题转化为代数问题;最后,把所有的代数问题转化为方程问题。
---笛卡儿(法国)
2x+3=0
2x+3y=6
FAMILY
方程大家庭
2x+3=0
2x+3y=0
一元一次方程
二元一次方程
分式方程
2x+3=0
2x+3y=6
FAMILY
方程大家庭
2x+3=0
2x+3y=0
一元一次方程
二元一次方程
分式方程
2x+3=0
2x+3y=6
FAMILY
方程大家庭
2x+3=0
一元一次方程
定义:只含有一个未知数,
未知数的次数是一次的整式方程。
探究新知
分享快乐
走近生活
问题情景(1)问题情景(1)
问题1 请列出方程:
数学来源于生活
数学化
问题情景(1)问题情景(1)
解:如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m,宽为 m,根据题意,可得方程:
(8-2x)
(5-2x)
(8 - 2x) (5 - 2x) = 18.
5m
8m
(8-2x)
(5-2x)
x
x
x
x
问题1 请列出方程:
数学来源于生活
观察下面等式:
102+112+122=132+142
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为: , , _______, .
x+1
x +2
x +3
x +4
根据题意,可得方程:
.
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
问题情景(2)问题情景(2)
问题2 请列出方程:
数学来源于生活
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
由勾股定理可知,滑动前梯子底端距墙 ____m .
如果设梯子底端滑动X m,那么滑动后梯子底端距墙
m;
根据题意,可得方程:
X+6
72+(X+6)2=102
xm
8m
10m
7m
6m
数学化
1m
问题情景(3)问题情景(3)
6
6m
问题3 请列出方程:
数学来源于生活
你能化简这三个方程吗?方程 ①②③有何特点
x2-12x-15=0
① (8-2x)(5-2x)=18
一元一次方程定义:只含有一个未知数,未知数的次数是一次的整式方程。
一元二次方程
(1)方程两边都是整式
(2)只含有一个未知数
(3)未知数的最高次数是2次
②x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
x2 - 8x-20=0.
2X2-13x+11=0
③72+(X+6)2=102
(4)都可以化成ax2+bx+c=0(a≠0)的形式
一元二次方程
(1)方程两边都是整式
(2)只含有一个未知数
(3)未知数的最高次数是2次
方程 ①②③有何特点
③72+(X+6)2=102 x2-12x-15=0
① (8-2x)(5-2x)=18 2X2-13x+11=0
像这样,只含有一个未知数的整式方程,且都可化成ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做 一元二次方程.
②x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
x2 - 8x-20=0.
(4)都可以化成ax2+bx+c=0(a≠0)的形式
(a≠0,a,b,c为常数)
ax2+ bx +c =0
二次项:ax2 一次项:bx 常数项:c
一元二次方程的一般形式
二次项系数
a
一次项系数
b
常数项
c
(a≠0,a,b,c为常数)
ax2+ bx +c =0
二次项:ax2 一次项:bx 常数项:c
一元二次方程的一般形式
二次项系数
a
一次项系数
b
常数项
c
想一想
为什么要限制a≠0
1.当b=0时
a≠0
2.当c=0时
3.当b=0,c=0时
一元二次方程的特殊形式
ax2+c=0
ax2+bx=0
ax2=0
b、c可以为零吗?
例1:下列方程是一元二次方程的是:
应用新知
(4)
(3)
(2)
(1)
判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②x2= x2- 4x ( )
③ 2xy-7=0 ( ) ④ ( )
1
x2
-
2
x
=0
⑤ ax2 + bx +c=0( )
慧眼找对错
自己编一个一元二次方程
例2:把下列方程化成一般形式,并指出二次项系数,一次项系数和常数项.
一般形式:ax +bx+c=0(a≠0)
应用新知
方程 一般形式 二次项系数 一次项系数 常数项
X2-4x-3=0
(x+1)2= (2x)2
X2-4x-3=0
1
- 4
-3
0.5
0
3x2-2x-1=0
3
-2
-1
-4
-3
抢答
注意
1、整理后书写一元二次方程时,通常降幂排列。
一般情况下,二次项系数应化为正数。
2、系数前面的符号不能丢。
已知关于x的方程(k2-1)x2 +2(k-1)x+3=0
(2)请你写出一个K的值,使原方程为一元一次方程这样的K值唯一吗?
(1)请你写出一个k的值,使原方程为一元二次方程,这样的K值有多少个?
K可以取任意实数吗?若不是,K要受到什么条件的限制?
比一比,哪个小组合作最佳?
k2-1≠0 即K≠±1
即K=-1
k2-1=0
K-1≠0
例3:关于x的方程 (a-2)x|a| -bx+3=0,
a,b为何值,此方程为一元二次方程
拓展延伸
解:(1) a-2≠0
|a|=2
∴a=-2,b是任意实数时是一元二次方程;
a≠2
a=± 2
新知
注意
困惑
感悟
预测方向
体会分享
1.一元二次方程的概念
2.一元二次方程的一般形式
(a≠0,a,b,c为常数)
数学问题
转化
实际问题
方程思想的应用
体会分享
4.两种思想:
类比
一元二次方程
①方程两边都是整式②只含有一个未知数
③未知数的最高次数是2次
3.根据定义确定字母系数的值
一元一次方程
1.请问下列方程哪些是一元二次方程 若是,指出各项的系数
(1)2x2-5xy+6y=0
(4)x2+2x-3=1+x2
你认识一元二次方程了吗?
( )
( )
( )
( )
(3) =0
(2)2x2- -1 =0
课堂 达标检测
2、你能找到五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
解:设五个连续整数中第一个数为x,
则后面四个数依次为_____、_____
_____、______。
根据题意可得方程为:
—————————————————————
X+1
X+2
X+3
X+4
(X+1)2
(X+2)2
+
(X+3)2
(X+4)2
=
+
X2
+
课堂达标检测
3.把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:
方 程 一般形式 二次项 系 数 一次项 系 数 常数项
3x2=5x-1
(x+2)(x -2)=6
4x-x2=0
课堂达标检测
3x2-5x+1=0
x2-10=0
x2-4x=0
3
1
1
-5
0
-4
1
-10
0
4、选做:
关于x的方程(m-2)x|m|+3mx+1=0是
一元二次方程,则 m= .
课堂达标检测
-2
(x-4)2+ (x-2)2= x2
5.从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺,另一个醉汉教他沿着门框的对角线拿进去。这个醉汉一试,刚好进去.你知道竹竿有多长吗 请根据这一问题列出方程.
即 x2-12 x +20 = 0
解:设竹竿的长为x尺,则门的宽 度为 尺,长为 尺,依题意得方程:
(x-4)
(x-2)
课堂达标检测
必做题:配套练习册P60-62
选做题:5
作业目的:1、进一步巩固一元二次方程的定义及一般形式。2、一元二次方程的实际应用。
作业要求:独立用心完成,保证准确率。
作业布置
给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
---- 高斯
美言分享
谢谢聆听
