2.7 闭合电路的欧姆定律 课件(人教选修3-1)
文档属性
| 名称 | 2.7 闭合电路的欧姆定律 课件(人教选修3-1) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-12-28 15:29:26 | ||
图片预览









文档简介
(共71张PPT)
名师课堂
·一点通
第二章
恒定电流
新知预习·巧设计
要点一
要点二
第7节
闭合电路的欧姆定律
创新演练
·大冲关
随堂检测归纳小结
课下作业综合提升
要点三
要点四
1.能够推导出闭合电路的欧姆定律
及其公式,知道电源的电动势等
于内、外电路上电势降落之和。
2.理解路端电压与负载的关系,
并能用欧姆定律进行电路的分
析和计算。
3.掌握电源的功率、输出功率及内阻
的消耗功率,并能熟练地用能的
观点来解决闭合电路的有关问题。
[读教材·填要点]
1.闭合电路的欧姆定律
(1)闭合电路组成:
①外电路:是指电源外部由 和 组成的电路。在外电路中沿电流方向电势 。
②内电路:是指电源内部的电路。在内电路中,沿电流方向电势 。
用电器
导线
降低
升高
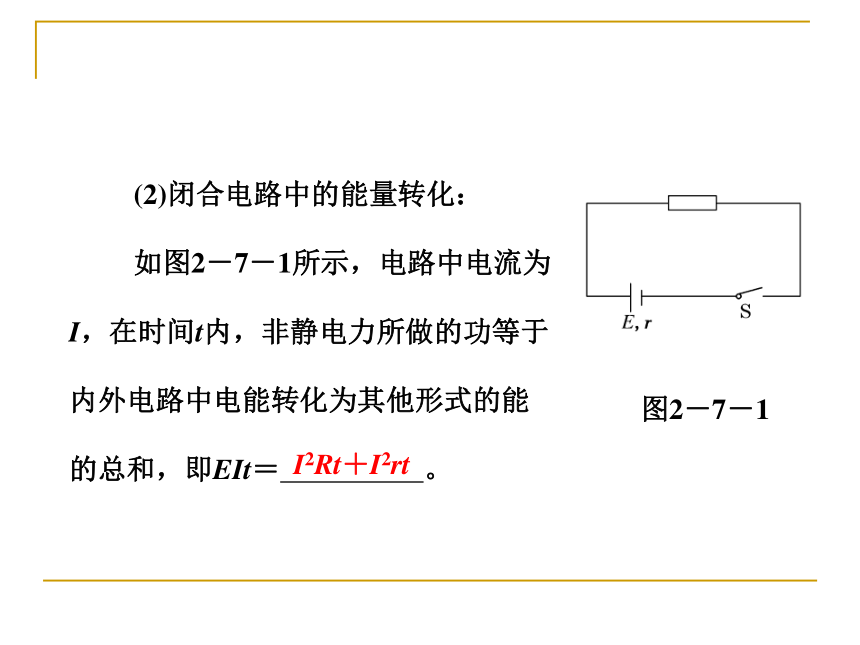
(2)闭合电路中的能量转化:
如图2-7-1所示,电路中电流为
I,在时间t内,非静电力所做的功等于
内外电路中电能转化为其他形式的能
的总和,即EIt= 。
I2Rt+I2rt
图2-7-1
正比
反比
纯电阻
E-Ir
U外
[关键一点] 在闭合电路中只有纯电阻电路中才存在IEt=I2Rt+I2rt的能量关系,若为非纯电阻电路,只能有IEt=IUt+I2rt。
增大
(2)路端电压与电流关系:
①公式:U= 。
②图像(U-I图像):如图2-7-2
所示是一条倾斜的直线,该直线与纵
轴交点的坐标表示 ,斜率的绝对值表示 。
E-Ir
电动势E
图2-7-2
电源内阻r
[关键一点] 用电压表直接测得的电源两端的电压,小于电源的电动势,因为电压表的内阻实际不是无穷大。
[试身手·夯基础]
1.只有用导线把电源、用电器连成一个________电路,电
路中才有电流,用电器、电线组成________电路,电源内部是________电路。在外电路中,正电荷在________的作用下由正极移到负极,在电源中________把正电荷从负极移动到正极。电流方向:在外电路上从________极到_______极,在电源内部从_______极到_______极。
答案:闭合 外 内 电场力 非静电力 电源正 电源负 电源负 电源正
2.电源内部的电路,其电阻为内电阻,内电阻所降落的
电压称为______;电源外部的电路,其两端电压称为________或________电压。电动势与内、外电压的关系可表示成:________,该式适用于任何闭合电路。
答案:内电压 外电压 路端 E=U外+U内
3.某闭合电路的路端电压与电流的
关系图像如图2-7-3所示,由
图知,闭合电路中的电源的电
动势为________,电源的内电
阻为________。
图2-7-3
答案:2 V 4 Ω
答案:A
1.确定电源的电动势和内阻
(1)由E=U+Ir知,只要知道两组U、I的值(U1、I1,U2、I2),就可以通过解方程组,求出E、r的值。
2.解决闭合电路问题的一般步骤
(1)分析电路:认清各元件的串、并联关系,必要时画等效电路图,特别注意电压表和电流表对应的电路。
(2)求总电流I:若已知内、外电路上所有电阻的阻值和电源电动势,可用闭合电路欧姆定律直接求出;若内、外电路上有多个未知电阻,可利用某一部分电路的已知电流和电压求总电流I;当以上方法都行不通时,可以应用联立方程求出I。
(3)各部分的电压、电流:根据串、并联电路的特点或部分电路欧姆定律求各部分电路的电压和电流。
(4)注意适用条件:外电路含有非纯电阻元件时(如电动机、电解槽等),不能直接用欧姆定律解决电流问题,可以根据串、并联电路特点或能量守恒定律进行列式计算。
[名师点睛] 不特殊指明时,电压表内阻可认为无穷大(相当于断路)。电流表的内阻认为是零(即相当于导线)。
1.如图2-7-4所示的电路中,
当S闭合时,电压表和电流表(理想电
表)的读数分别为1.6 V和0.4 A,当S
断开时,它们的示数变为1.7 V和0.3
A,则电源的电动势和内阻各为多少?
图2-7-4
[审题指导]
(1)明确S闭合前后R1和R2的连接方式。
(2)明确电压表所测电压为路端电压。
[解析] 当S闭合时,R1和R2并联接入电路,由闭合电路欧姆定律得:U端1=E-I1r,代入数据得:E=1.6+0.4r①
当S断开时,只有R1接入电路,由闭合电路欧姆定律得:U端2=E-I2r,
代入数据得:E=1.7+0.3r②
联立①②得:E=2 V,r=1 Ω
[答案] 2 V 1 Ω
解决这类问题应该充分利用题设条件,结合闭合电路欧姆定律列方程求解,在求解过程中要注意电流的变化,因为电流是连接内外电路的纽带。
闭合电路中只要有一只电阻的阻值发生变化,就会影响整个电路,使总电路和每一部分的电流、电压都发生变化。其分析的一般思路为:
(1)确定电路的外电阻R外总如何变化:①当外电路的任何一个电阻增大(或减小)时,电路的总电阻一定增大(或减小);②若电键的闭合使串联的用电器增多,总电阻增大;若电键的闭合使并联的支路增多,总电阻减小。
(5)由部分电路欧姆定律确定干路上某定值电阻两端的电压如何变化。
(6)确定支路两端电压如何变化以及通过各支路的电流如何变化(可利用串联电路的电压关系、并联电路的电流关系)。
[名师点睛] 电路中任一电阻增大(减小),则该电阻两端的电压一定会增大(减小),而通过该电阻的电流会减小(增大)。
2.(2011·海南高考)如图2-7-5 ,
E为内阻不能忽略的电池,R1、R2、
R3为定值电阻,S0、S为开关, 与
分别为电压表与电流表。初始时
S0与S均闭合,现将S断开,则( )
图2-7-5
A. 的读数变大, 的读数变小
B. 的读数变大, 的读数变大
C. 的读数变小, 的读数变小
D. 的读数变小, 的读数变大
[解析] S断开相当于电阻变大,总电流减小,故端电压增大, 的读数变大,把R1归为内阻,则R3中的电压也增大,R3中的电流也增大,电流表示数变大,故B正确。
[答案] B
此类问题解题思路是:先判断电阻变化情况,然后根据I=E/(R+r)判断电流变化情况,再判断路端电压变化情况,然后根据串、并联的知识判断电表示数变化或某一电阻、用电器等电流、电压和功率的变化。
图2-7-6
[名师点睛] 当R=r时,电源的输出功率最大,但效率仅为50%,只有外电路断路时电源的效率才可能达到100%。
3.如图2-7-7所示,线段A为
某电源的U-I图线,线段B为某电阻
的U-I图线,当上述电源和电阻组
成闭合电路时,求:
图2-7-7
(1)电源的输出功率P出多大?
(2)电源内部损耗的电功率是多少?
(3)电源的效率η多大?
[思路点拨] 对图像问题要做到四看:看横、纵坐标轴上的截距,看图线的斜率,看图像的交点,在此基础上进行正确的分析判断。
[答案] (1)4 W (2)2 W (3)66.7 %
电源的U-I图线与电阻的U-I图线的物理意义不同,前者是路端电压与电路电流的函数关系;后者是加在电阻两端的电压与通过的电流的函数关系。从图像中能知道哪些物理量及从两个图像能求出哪些物理量是解题的关键。
电容器是一个储存电能的元件。在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大的元件,在电容器处电路看作是断路,画等效电路时,可以先把它去掉。
1.分析和计算含有电容器的直流电路
(1)电路稳定时:电容器所在支路相当于断路。因此,该支路上的电阻两端无电压,该电阻相当于导线。
(2)当电容器与电阻并联后接入电路时:电容器两端的电压与并联电阻两端的电压相等。
(3)电路中的电流、电压变化时:将会引起电容器的充放电。如果电容器两端的电压升高,电容器将充电;反之电容器放电,通过与电容器串联的电阻的电荷量等于电容器带电量的变化。
2.解答含电容器电路问题的步骤
(1)应用电路的有关规律分析出电容器两极板间的电压及其变化情况。
(2)根据平行板电容器的相关知识进行分析求解。
图2-7-8
4.如图2-7-8所示,电容器
C1=6 μF,C2=3 μF,电阻R1=
6 Ω,R2=3 Ω。C、D为两端点,
当开关S断开时,A、B两点间的
电压UAB为多少?当S闭合时,电容器C1的电荷量改变了多少?(已知电压U=18 V)
[思路点拨] 与电容器串联的电阻两端等电势。
[解析] 在电路中电容器C1、C2的作用是断路,当开关S断开时,电路中无电流,B、C等电势,A、D等电势。
因此UAB=UAC=UDC=18 V。
当S断开时,电容器C1所带电荷量为
Q1=C1UAC=6×10-6×18 C=1.08×10-4 C。
Q1′=C1UAC′=6×10-6×12 C=0.72×10-4 C。
电容器C1所带电荷量的变化量为:
ΔQ=Q1′-Q1=-3.6×10-5 C。“-”号表示减少。
[答案] 18 V 减少了3.6×10-5 C
电容器极板间有绝缘介质,直流电流不能通过,因此电阻与电容器串联时,电阻无电流通过,电阻两端电压为零;电阻与电容器并联时,电容器两端电压与电阻两端电压相等。
1.(对应要点一)某电池当外电路断开时的路端电压为3 V,
接上8 Ω的负载电阻后其路端电压降为2.4 V,则可以断定该电池的电动势E和内阻r为 ( )
A.E=2.4 V r=1 Ω B.E=3 V r=2 Ω
C.E=2.4 V r=2 Ω D.E=3 V r=1 Ω
解析:由题知,电源的电动势为3 V,接入外电阻,外电压为2.4 V,I=U/R=0.3 A,由I=E/(R+r)解得r=2 Ω。
答案:B
2.(对应要点二)如图2-7-9所示,A、
B、C三只电灯均能发光,当把
滑动变阻器的触头P向下滑动时,
三只电灯亮度的变化是 ( )
A.A、B、C都变亮 B.A、B变亮,C变暗
C.A、C变亮,B变暗 D.A变亮,B、C变暗
图2-7-9
答案:B
3.(对应要点四)如图2-7-10所示,电
源电动势为E,它的内阻r=2 Ω,电
阻R1=28 Ω,R2=30 Ω,R3=60 Ω。
求开关S断开和闭合时,电容器所带
电荷量之比为 ( )
A.1∶1 B.2∶1
C.4∶1 D.1∶4
图2-7-10
答案:B
4.(对应要点三)如图2-7-11所示,电
源电动势E=10 V,内阻r=0.5 Ω,
“8 V 16 W”的灯泡L恰好能正常发光,
电动机线圈电阻R0=1 Ω,求:
(1)路端电压。
(2)电源的总功率。
(3)电动机的输出功率。
图2-7-11
答案:(1)8 V (2)40 W (3)12 W
(1)闭合电路的欧姆定律是电路分析的基本定律,利用该定律既可以分析一般问题,也可以进行动态分析以及含容电路分析。
(2)闭合电路的欧姆定律实质上是能量守恒在电路中的体现。在分析问题时应注意电路情况:纯电阻电路和非纯电阻电路。
(3)闭合电路的欧姆定律也为生产、生活中的电路设计提供了依据。
点击下图进入“课下作业综合提升”
名师课堂
·一点通
第二章
恒定电流
新知预习·巧设计
要点一
要点二
第7节
闭合电路的欧姆定律
创新演练
·大冲关
随堂检测归纳小结
课下作业综合提升
要点三
要点四
1.能够推导出闭合电路的欧姆定律
及其公式,知道电源的电动势等
于内、外电路上电势降落之和。
2.理解路端电压与负载的关系,
并能用欧姆定律进行电路的分
析和计算。
3.掌握电源的功率、输出功率及内阻
的消耗功率,并能熟练地用能的
观点来解决闭合电路的有关问题。
[读教材·填要点]
1.闭合电路的欧姆定律
(1)闭合电路组成:
①外电路:是指电源外部由 和 组成的电路。在外电路中沿电流方向电势 。
②内电路:是指电源内部的电路。在内电路中,沿电流方向电势 。
用电器
导线
降低
升高
(2)闭合电路中的能量转化:
如图2-7-1所示,电路中电流为
I,在时间t内,非静电力所做的功等于
内外电路中电能转化为其他形式的能
的总和,即EIt= 。
I2Rt+I2rt
图2-7-1
正比
反比
纯电阻
E-Ir
U外
[关键一点] 在闭合电路中只有纯电阻电路中才存在IEt=I2Rt+I2rt的能量关系,若为非纯电阻电路,只能有IEt=IUt+I2rt。
增大
(2)路端电压与电流关系:
①公式:U= 。
②图像(U-I图像):如图2-7-2
所示是一条倾斜的直线,该直线与纵
轴交点的坐标表示 ,斜率的绝对值表示 。
E-Ir
电动势E
图2-7-2
电源内阻r
[关键一点] 用电压表直接测得的电源两端的电压,小于电源的电动势,因为电压表的内阻实际不是无穷大。
[试身手·夯基础]
1.只有用导线把电源、用电器连成一个________电路,电
路中才有电流,用电器、电线组成________电路,电源内部是________电路。在外电路中,正电荷在________的作用下由正极移到负极,在电源中________把正电荷从负极移动到正极。电流方向:在外电路上从________极到_______极,在电源内部从_______极到_______极。
答案:闭合 外 内 电场力 非静电力 电源正 电源负 电源负 电源正
2.电源内部的电路,其电阻为内电阻,内电阻所降落的
电压称为______;电源外部的电路,其两端电压称为________或________电压。电动势与内、外电压的关系可表示成:________,该式适用于任何闭合电路。
答案:内电压 外电压 路端 E=U外+U内
3.某闭合电路的路端电压与电流的
关系图像如图2-7-3所示,由
图知,闭合电路中的电源的电
动势为________,电源的内电
阻为________。
图2-7-3
答案:2 V 4 Ω
答案:A
1.确定电源的电动势和内阻
(1)由E=U+Ir知,只要知道两组U、I的值(U1、I1,U2、I2),就可以通过解方程组,求出E、r的值。
2.解决闭合电路问题的一般步骤
(1)分析电路:认清各元件的串、并联关系,必要时画等效电路图,特别注意电压表和电流表对应的电路。
(2)求总电流I:若已知内、外电路上所有电阻的阻值和电源电动势,可用闭合电路欧姆定律直接求出;若内、外电路上有多个未知电阻,可利用某一部分电路的已知电流和电压求总电流I;当以上方法都行不通时,可以应用联立方程求出I。
(3)各部分的电压、电流:根据串、并联电路的特点或部分电路欧姆定律求各部分电路的电压和电流。
(4)注意适用条件:外电路含有非纯电阻元件时(如电动机、电解槽等),不能直接用欧姆定律解决电流问题,可以根据串、并联电路特点或能量守恒定律进行列式计算。
[名师点睛] 不特殊指明时,电压表内阻可认为无穷大(相当于断路)。电流表的内阻认为是零(即相当于导线)。
1.如图2-7-4所示的电路中,
当S闭合时,电压表和电流表(理想电
表)的读数分别为1.6 V和0.4 A,当S
断开时,它们的示数变为1.7 V和0.3
A,则电源的电动势和内阻各为多少?
图2-7-4
[审题指导]
(1)明确S闭合前后R1和R2的连接方式。
(2)明确电压表所测电压为路端电压。
[解析] 当S闭合时,R1和R2并联接入电路,由闭合电路欧姆定律得:U端1=E-I1r,代入数据得:E=1.6+0.4r①
当S断开时,只有R1接入电路,由闭合电路欧姆定律得:U端2=E-I2r,
代入数据得:E=1.7+0.3r②
联立①②得:E=2 V,r=1 Ω
[答案] 2 V 1 Ω
解决这类问题应该充分利用题设条件,结合闭合电路欧姆定律列方程求解,在求解过程中要注意电流的变化,因为电流是连接内外电路的纽带。
闭合电路中只要有一只电阻的阻值发生变化,就会影响整个电路,使总电路和每一部分的电流、电压都发生变化。其分析的一般思路为:
(1)确定电路的外电阻R外总如何变化:①当外电路的任何一个电阻增大(或减小)时,电路的总电阻一定增大(或减小);②若电键的闭合使串联的用电器增多,总电阻增大;若电键的闭合使并联的支路增多,总电阻减小。
(5)由部分电路欧姆定律确定干路上某定值电阻两端的电压如何变化。
(6)确定支路两端电压如何变化以及通过各支路的电流如何变化(可利用串联电路的电压关系、并联电路的电流关系)。
[名师点睛] 电路中任一电阻增大(减小),则该电阻两端的电压一定会增大(减小),而通过该电阻的电流会减小(增大)。
2.(2011·海南高考)如图2-7-5 ,
E为内阻不能忽略的电池,R1、R2、
R3为定值电阻,S0、S为开关, 与
分别为电压表与电流表。初始时
S0与S均闭合,现将S断开,则( )
图2-7-5
A. 的读数变大, 的读数变小
B. 的读数变大, 的读数变大
C. 的读数变小, 的读数变小
D. 的读数变小, 的读数变大
[解析] S断开相当于电阻变大,总电流减小,故端电压增大, 的读数变大,把R1归为内阻,则R3中的电压也增大,R3中的电流也增大,电流表示数变大,故B正确。
[答案] B
此类问题解题思路是:先判断电阻变化情况,然后根据I=E/(R+r)判断电流变化情况,再判断路端电压变化情况,然后根据串、并联的知识判断电表示数变化或某一电阻、用电器等电流、电压和功率的变化。
图2-7-6
[名师点睛] 当R=r时,电源的输出功率最大,但效率仅为50%,只有外电路断路时电源的效率才可能达到100%。
3.如图2-7-7所示,线段A为
某电源的U-I图线,线段B为某电阻
的U-I图线,当上述电源和电阻组
成闭合电路时,求:
图2-7-7
(1)电源的输出功率P出多大?
(2)电源内部损耗的电功率是多少?
(3)电源的效率η多大?
[思路点拨] 对图像问题要做到四看:看横、纵坐标轴上的截距,看图线的斜率,看图像的交点,在此基础上进行正确的分析判断。
[答案] (1)4 W (2)2 W (3)66.7 %
电源的U-I图线与电阻的U-I图线的物理意义不同,前者是路端电压与电路电流的函数关系;后者是加在电阻两端的电压与通过的电流的函数关系。从图像中能知道哪些物理量及从两个图像能求出哪些物理量是解题的关键。
电容器是一个储存电能的元件。在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大的元件,在电容器处电路看作是断路,画等效电路时,可以先把它去掉。
1.分析和计算含有电容器的直流电路
(1)电路稳定时:电容器所在支路相当于断路。因此,该支路上的电阻两端无电压,该电阻相当于导线。
(2)当电容器与电阻并联后接入电路时:电容器两端的电压与并联电阻两端的电压相等。
(3)电路中的电流、电压变化时:将会引起电容器的充放电。如果电容器两端的电压升高,电容器将充电;反之电容器放电,通过与电容器串联的电阻的电荷量等于电容器带电量的变化。
2.解答含电容器电路问题的步骤
(1)应用电路的有关规律分析出电容器两极板间的电压及其变化情况。
(2)根据平行板电容器的相关知识进行分析求解。
图2-7-8
4.如图2-7-8所示,电容器
C1=6 μF,C2=3 μF,电阻R1=
6 Ω,R2=3 Ω。C、D为两端点,
当开关S断开时,A、B两点间的
电压UAB为多少?当S闭合时,电容器C1的电荷量改变了多少?(已知电压U=18 V)
[思路点拨] 与电容器串联的电阻两端等电势。
[解析] 在电路中电容器C1、C2的作用是断路,当开关S断开时,电路中无电流,B、C等电势,A、D等电势。
因此UAB=UAC=UDC=18 V。
当S断开时,电容器C1所带电荷量为
Q1=C1UAC=6×10-6×18 C=1.08×10-4 C。
Q1′=C1UAC′=6×10-6×12 C=0.72×10-4 C。
电容器C1所带电荷量的变化量为:
ΔQ=Q1′-Q1=-3.6×10-5 C。“-”号表示减少。
[答案] 18 V 减少了3.6×10-5 C
电容器极板间有绝缘介质,直流电流不能通过,因此电阻与电容器串联时,电阻无电流通过,电阻两端电压为零;电阻与电容器并联时,电容器两端电压与电阻两端电压相等。
1.(对应要点一)某电池当外电路断开时的路端电压为3 V,
接上8 Ω的负载电阻后其路端电压降为2.4 V,则可以断定该电池的电动势E和内阻r为 ( )
A.E=2.4 V r=1 Ω B.E=3 V r=2 Ω
C.E=2.4 V r=2 Ω D.E=3 V r=1 Ω
解析:由题知,电源的电动势为3 V,接入外电阻,外电压为2.4 V,I=U/R=0.3 A,由I=E/(R+r)解得r=2 Ω。
答案:B
2.(对应要点二)如图2-7-9所示,A、
B、C三只电灯均能发光,当把
滑动变阻器的触头P向下滑动时,
三只电灯亮度的变化是 ( )
A.A、B、C都变亮 B.A、B变亮,C变暗
C.A、C变亮,B变暗 D.A变亮,B、C变暗
图2-7-9
答案:B
3.(对应要点四)如图2-7-10所示,电
源电动势为E,它的内阻r=2 Ω,电
阻R1=28 Ω,R2=30 Ω,R3=60 Ω。
求开关S断开和闭合时,电容器所带
电荷量之比为 ( )
A.1∶1 B.2∶1
C.4∶1 D.1∶4
图2-7-10
答案:B
4.(对应要点三)如图2-7-11所示,电
源电动势E=10 V,内阻r=0.5 Ω,
“8 V 16 W”的灯泡L恰好能正常发光,
电动机线圈电阻R0=1 Ω,求:
(1)路端电压。
(2)电源的总功率。
(3)电动机的输出功率。
图2-7-11
答案:(1)8 V (2)40 W (3)12 W
(1)闭合电路的欧姆定律是电路分析的基本定律,利用该定律既可以分析一般问题,也可以进行动态分析以及含容电路分析。
(2)闭合电路的欧姆定律实质上是能量守恒在电路中的体现。在分析问题时应注意电路情况:纯电阻电路和非纯电阻电路。
(3)闭合电路的欧姆定律也为生产、生活中的电路设计提供了依据。
点击下图进入“课下作业综合提升”
