北师大版八年级数学下册 3.1 平面图形的镶嵌 课件 (共25张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 3.1 平面图形的镶嵌 课件 (共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 16:13:28 | ||
图片预览




文档简介
(共25张PPT)
北师大版初中数学
八下—综合与实践
生活中的正多边形图案
在铺地板砖时应注意什么?砖与砖之间是否有空隙,是否重叠?
没有空隙,不重叠
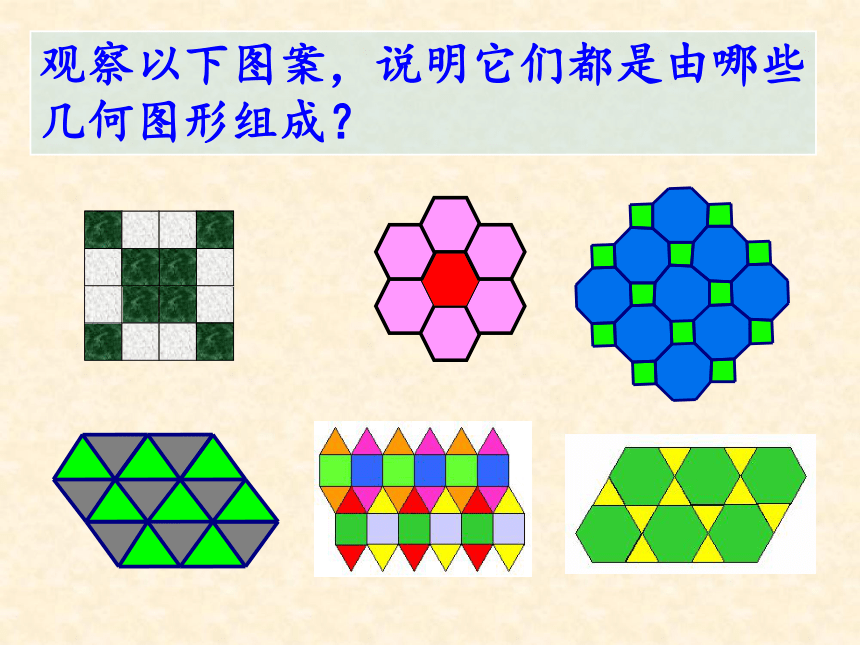
观察以下图案,说明它们都是由哪些几何图形组成?
它们都有哪些共同的特征?
没有空隙,不重叠
平面图形的镶嵌
现实生活中的问题
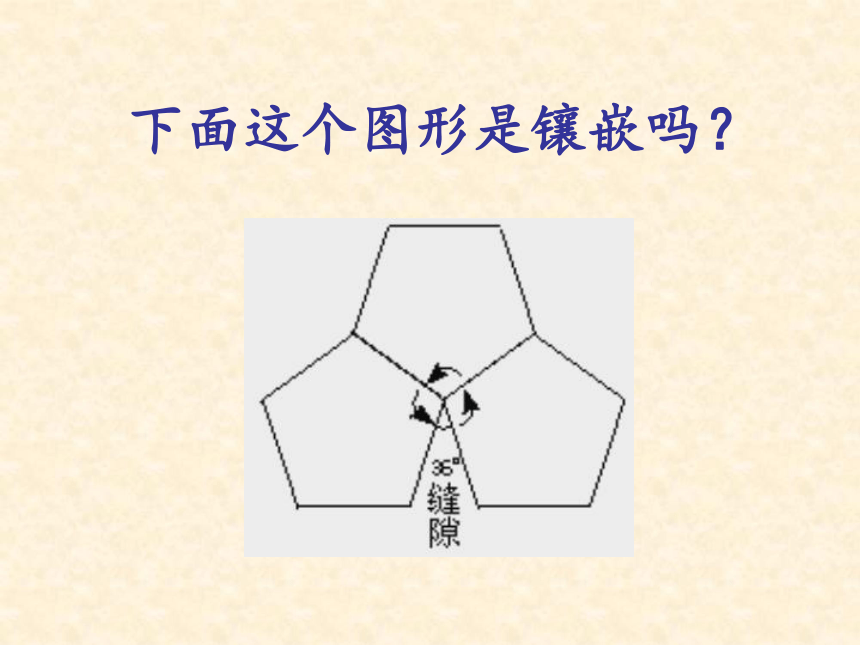
下面这个图形是镶嵌吗?
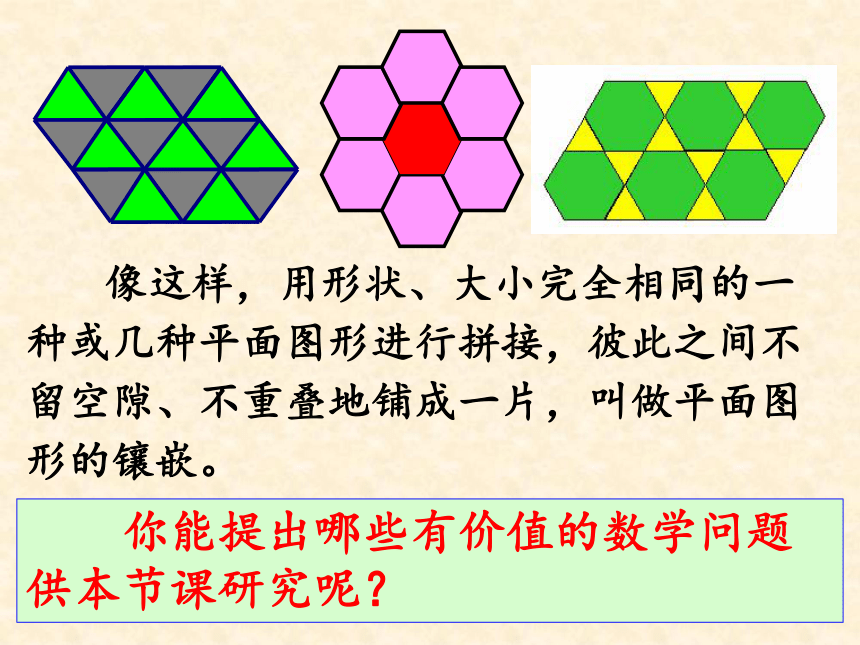
像这样,用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,叫做平面图形的镶嵌。
你能提出哪些有价值的数学问题供本节课研究呢?
小组活动:
画图或利用课前准备好的纸片,动手操作,验证自已的猜想。看哪个小组拼得又快又好!
猜一猜:哪些正多边形通过拼接能进行平面的镶嵌?
60°
60°
60°
60°
60°
60°
90°
1、边长相等。
2、每个公共顶点处几个内角的和为360°。
平面镶嵌的条件
120 °
120 °
120 °
观察以上图形,思考:
镶嵌时如何做到既无缝隙又不重叠
用同一种正多边形进行平面镶嵌,只有正三角形、正四边形、正六边形三种图形才行。
观察能镶嵌的三种图形,你发现
它们与平移、旋转、对称有什么关系?
60°
60°
60°
60°
60°
60°
90°
120 °
120 °
120 °
整个图案可以由一个基本图形通过平移、旋转或对称得到。
——平面图形镶嵌的本质
1、同一种任意三角形能否镶嵌?
2、四边形呢
同一种任意三角形可以镶嵌。
1
2
3
4
同一种任意四边形可以镶嵌。
小组活动:
哪两种正多边形组合在一起能进行镶嵌?看谁拼得最多?
(1)正三角形与正方形的平面镶嵌
(2)正三角形与正六边形的平面镶嵌
(3)正四边形与正八边形的平面镶嵌
只要满足边长相等和每个公共顶点处几个内角的和为360°,两个正多边形就能进行镶嵌.
它们有什么共同的特征?
看老师变魔术啦!
胜利之星
看老师变魔术啦!
漂亮的窗户
通向成功的小路
问1:平面图形的镶嵌的本质及条件是什么?
问2:如何设计镶嵌的美丽图案?
1:平面图形镶嵌的条件是边长相等且每个公共顶点处几个内角的和为360°。本质就是数学知识中的平移、旋转、对称在实际生活中的综合应用。
2:利用平面图形镶嵌的定义和对称、旋转、平移的数学方法可以设计一些简单的漂亮的平面镶嵌的图案。
请
欣
赏
1、非正多边形能否进行平面镶嵌?
2、结合本节课写一篇关于平面镶嵌的实验报告或一篇小论文。
3、根据自己的爱好,设计一个美丽的平面镶嵌图案。
4、请到网上查找平面镶嵌图形的有关内容。
北师大版初中数学
八下—综合与实践
生活中的正多边形图案
在铺地板砖时应注意什么?砖与砖之间是否有空隙,是否重叠?
没有空隙,不重叠
观察以下图案,说明它们都是由哪些几何图形组成?
它们都有哪些共同的特征?
没有空隙,不重叠
平面图形的镶嵌
现实生活中的问题
下面这个图形是镶嵌吗?
像这样,用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,叫做平面图形的镶嵌。
你能提出哪些有价值的数学问题供本节课研究呢?
小组活动:
画图或利用课前准备好的纸片,动手操作,验证自已的猜想。看哪个小组拼得又快又好!
猜一猜:哪些正多边形通过拼接能进行平面的镶嵌?
60°
60°
60°
60°
60°
60°
90°
1、边长相等。
2、每个公共顶点处几个内角的和为360°。
平面镶嵌的条件
120 °
120 °
120 °
观察以上图形,思考:
镶嵌时如何做到既无缝隙又不重叠
用同一种正多边形进行平面镶嵌,只有正三角形、正四边形、正六边形三种图形才行。
观察能镶嵌的三种图形,你发现
它们与平移、旋转、对称有什么关系?
60°
60°
60°
60°
60°
60°
90°
120 °
120 °
120 °
整个图案可以由一个基本图形通过平移、旋转或对称得到。
——平面图形镶嵌的本质
1、同一种任意三角形能否镶嵌?
2、四边形呢
同一种任意三角形可以镶嵌。
1
2
3
4
同一种任意四边形可以镶嵌。
小组活动:
哪两种正多边形组合在一起能进行镶嵌?看谁拼得最多?
(1)正三角形与正方形的平面镶嵌
(2)正三角形与正六边形的平面镶嵌
(3)正四边形与正八边形的平面镶嵌
只要满足边长相等和每个公共顶点处几个内角的和为360°,两个正多边形就能进行镶嵌.
它们有什么共同的特征?
看老师变魔术啦!
胜利之星
看老师变魔术啦!
漂亮的窗户
通向成功的小路
问1:平面图形的镶嵌的本质及条件是什么?
问2:如何设计镶嵌的美丽图案?
1:平面图形镶嵌的条件是边长相等且每个公共顶点处几个内角的和为360°。本质就是数学知识中的平移、旋转、对称在实际生活中的综合应用。
2:利用平面图形镶嵌的定义和对称、旋转、平移的数学方法可以设计一些简单的漂亮的平面镶嵌的图案。
请
欣
赏
1、非正多边形能否进行平面镶嵌?
2、结合本节课写一篇关于平面镶嵌的实验报告或一篇小论文。
3、根据自己的爱好,设计一个美丽的平面镶嵌图案。
4、请到网上查找平面镶嵌图形的有关内容。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
