第26章圆测试题(无答案)
图片预览

文档简介
26圆单元测试题(沪科版)
姓名: 得分
填空题(每小题3分,共18分)
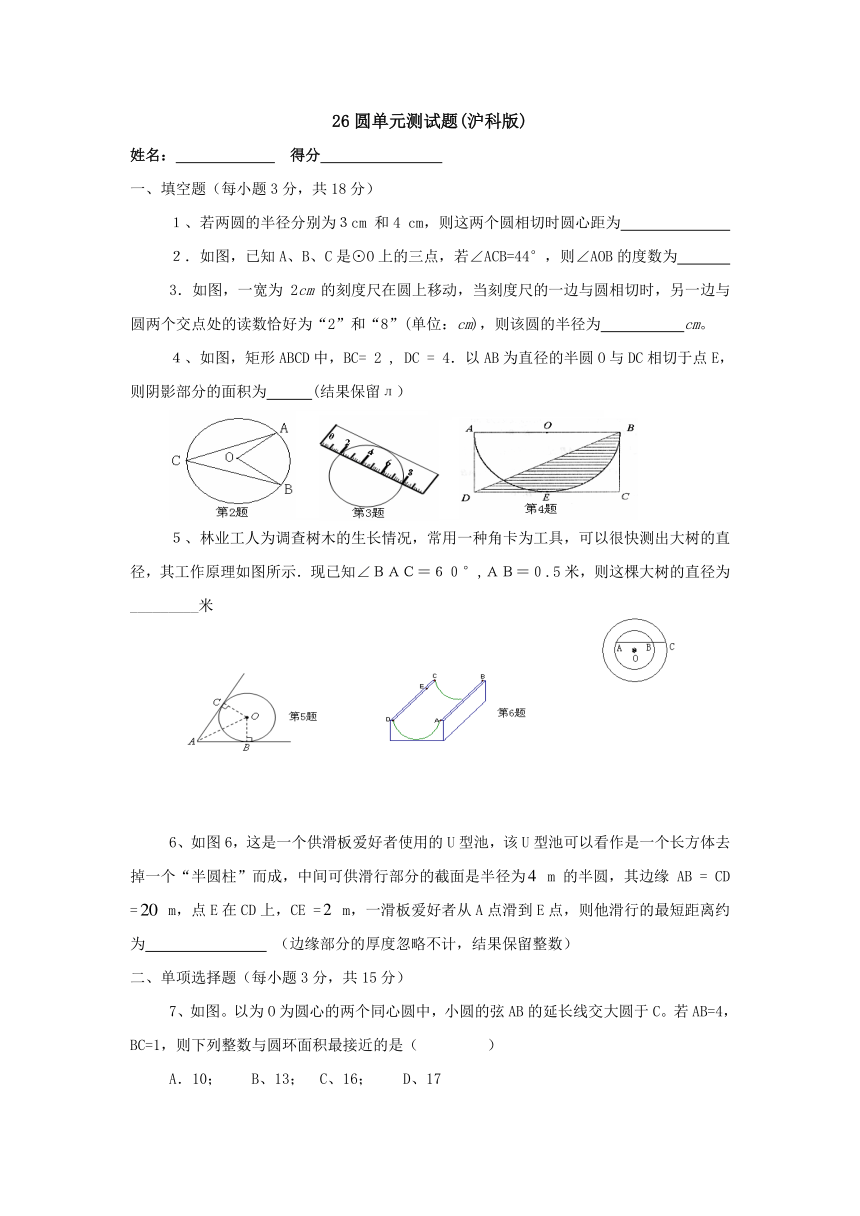
1、若两圆的半径分别为3cm 和4 cm,则这两个圆相切时圆心距为
2.如图,已知A、B、C是⊙O上的三点,若∠ACB=44°,则∠AOB的度数为
3.如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm。
4、如图,矩形ABCD中,BC= 2 , DC = 4.以AB为直径的半圆O与DC相切于点E,则阴影部分的面积为 (结果保留л)
5、林业工人为调查树木的生长情况,常用一种角卡为工具,可以很快测出大树的直径,其工作原理如图所示.现已知∠BAC=60°,AB=0.5米,则这棵大树的直径为_________米
6、如图6,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为 m的半圆,其边缘AB = CD = m,点E在CD上,CE = m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 (边缘部分的厚度忽略不计,结果保留整数)
单项选择题(每小题3分,共15分)
7、如图。以为O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于C。若AB=4,BC=1,则下列整数与圆环面积最接近的是( )
A.10; B、13; C、16; D、17
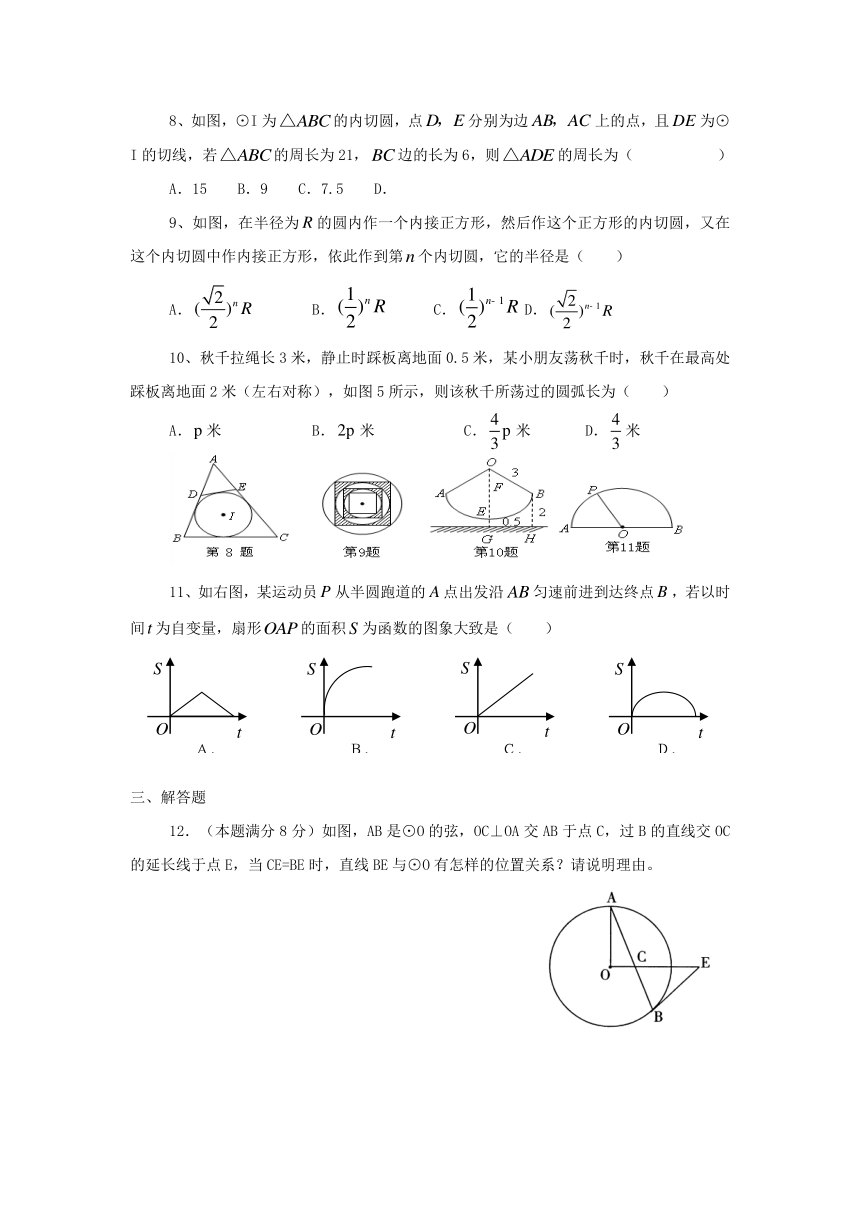
8、如图,⊙I为的内切圆,点分别为边上的点,且为⊙I的切线,若的周长为21,边的长为6,则的周长为( )
A.15 B.9 C.7.5 D.
9、如图,在半径为的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第个内切圆,它的半径是( )
A. B. C. D.
10、秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡秋千时,秋千在最高处踩板离地面2米(左右对称),如图5所示,则该秋千所荡过的圆弧长为( )
A.米 B.米 C.米 D.米
11、如右图,某运动员从半圆跑道的点出发沿匀速前进到达终点,若以时间为自变量,扇形的面积为函数的图象大致是( )
解答题
12.(本题满分8分)如图,AB是⊙O的弦,OC⊥OA交AB于点C,过B的直线交OC的延长线于点E,当CE=BE时,直线BE与⊙O有怎样的位置关系?请说明理由。
13.(本题满分8分)如图8,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB =,高BC =,求这个零件的表面积;(结果保留)
14.(本小题满分9分)如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA=。求:
(1)∠POA的度数;
(2)弦AB的长;
(3)阴影部分的面积。
15、(本小题满分6分)如图24—A—13,AD、BC是⊙O的两条弦,且AD=BC,
求证:AB=CD。
16、(本小题满分6分)如图24—A—14,已知⊙O的半径为8cm,点A为半径OB的延长线上一点,射线AC切⊙O于点C,BC的长为,求线段AB的长。
综合解答题(共50分)
17、(本小题满分7分)图18—1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图18—2是车棚顶部截面的示意图,所在圆的圆心为O.车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留л).
18、(本小题满分7分)如图,是⊙O1与⊙O2的公共弦,在⊙O2上,分别是⊙O1与⊙O2的直径,与的延长线交于点,与相交于点.
(1)连结,求证:;(2)求证:是⊙O1的切线;
19、(本小题满分9分)如图9,在相距的两个城镇之间,有一近似圆形的湖泊,其半径为,圆心恰好位于连线的中点处.现要绕过湖泊从城到城,假设除湖泊外,所有的地方均可行走,线段AC与线段长相等,其中在直线上.请你:1、设计二种行走路线, (4分),
2、找出最短的行走路线,并求出这条路线的长度.(5分)(结果精确到0.1米)()
20、(本小题满分8分)22.如图24—B—17,AB是⊙O的弦(非直径),C、D是AB上的两点,并且AC=BD。求证:OC=OD。
21、(本小题满分9分)已知Rt△ABC中,∠ACB=90°,AC=6,BC=8。
如图①,若半径为r1的⊙O1是Rt△ABC的内切圆,求r1;
22、(本小题满分3+3+4=10分)如图,在平面直角坐标系中,与轴交于两点,是的直径,过点的直线交轴于点,连结,已知点的坐标为,直线的函数解析式为.
(1)求点的坐标和的长;
(2)求点的坐标和的半径;
(3)求证:是的切线.
姓名: 得分
填空题(每小题3分,共18分)
1、若两圆的半径分别为3cm 和4 cm,则这两个圆相切时圆心距为
2.如图,已知A、B、C是⊙O上的三点,若∠ACB=44°,则∠AOB的度数为
3.如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm。
4、如图,矩形ABCD中,BC= 2 , DC = 4.以AB为直径的半圆O与DC相切于点E,则阴影部分的面积为 (结果保留л)
5、林业工人为调查树木的生长情况,常用一种角卡为工具,可以很快测出大树的直径,其工作原理如图所示.现已知∠BAC=60°,AB=0.5米,则这棵大树的直径为_________米
6、如图6,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为 m的半圆,其边缘AB = CD = m,点E在CD上,CE = m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 (边缘部分的厚度忽略不计,结果保留整数)
单项选择题(每小题3分,共15分)
7、如图。以为O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于C。若AB=4,BC=1,则下列整数与圆环面积最接近的是( )
A.10; B、13; C、16; D、17
8、如图,⊙I为的内切圆,点分别为边上的点,且为⊙I的切线,若的周长为21,边的长为6,则的周长为( )
A.15 B.9 C.7.5 D.
9、如图,在半径为的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第个内切圆,它的半径是( )
A. B. C. D.
10、秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡秋千时,秋千在最高处踩板离地面2米(左右对称),如图5所示,则该秋千所荡过的圆弧长为( )
A.米 B.米 C.米 D.米
11、如右图,某运动员从半圆跑道的点出发沿匀速前进到达终点,若以时间为自变量,扇形的面积为函数的图象大致是( )
解答题
12.(本题满分8分)如图,AB是⊙O的弦,OC⊥OA交AB于点C,过B的直线交OC的延长线于点E,当CE=BE时,直线BE与⊙O有怎样的位置关系?请说明理由。
13.(本题满分8分)如图8,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB =,高BC =,求这个零件的表面积;(结果保留)
14.(本小题满分9分)如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA=。求:
(1)∠POA的度数;
(2)弦AB的长;
(3)阴影部分的面积。
15、(本小题满分6分)如图24—A—13,AD、BC是⊙O的两条弦,且AD=BC,
求证:AB=CD。
16、(本小题满分6分)如图24—A—14,已知⊙O的半径为8cm,点A为半径OB的延长线上一点,射线AC切⊙O于点C,BC的长为,求线段AB的长。
综合解答题(共50分)
17、(本小题满分7分)图18—1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图18—2是车棚顶部截面的示意图,所在圆的圆心为O.车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留л).
18、(本小题满分7分)如图,是⊙O1与⊙O2的公共弦,在⊙O2上,分别是⊙O1与⊙O2的直径,与的延长线交于点,与相交于点.
(1)连结,求证:;(2)求证:是⊙O1的切线;
19、(本小题满分9分)如图9,在相距的两个城镇之间,有一近似圆形的湖泊,其半径为,圆心恰好位于连线的中点处.现要绕过湖泊从城到城,假设除湖泊外,所有的地方均可行走,线段AC与线段长相等,其中在直线上.请你:1、设计二种行走路线, (4分),
2、找出最短的行走路线,并求出这条路线的长度.(5分)(结果精确到0.1米)()
20、(本小题满分8分)22.如图24—B—17,AB是⊙O的弦(非直径),C、D是AB上的两点,并且AC=BD。求证:OC=OD。
21、(本小题满分9分)已知Rt△ABC中,∠ACB=90°,AC=6,BC=8。
如图①,若半径为r1的⊙O1是Rt△ABC的内切圆,求r1;
22、(本小题满分3+3+4=10分)如图,在平面直角坐标系中,与轴交于两点,是的直径,过点的直线交轴于点,连结,已知点的坐标为,直线的函数解析式为.
(1)求点的坐标和的长;
(2)求点的坐标和的半径;
(3)求证:是的切线.
