青岛版五四制四年级下册数学第二单元组合图形的面积课件(共39张PPT)
文档属性
| 名称 | 青岛版五四制四年级下册数学第二单元组合图形的面积课件(共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 54.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 13:32:47 | ||
图片预览






文档简介
(共39张PPT)
复习
ɑ
ɑ
b
ɑ
h
ɑ
h
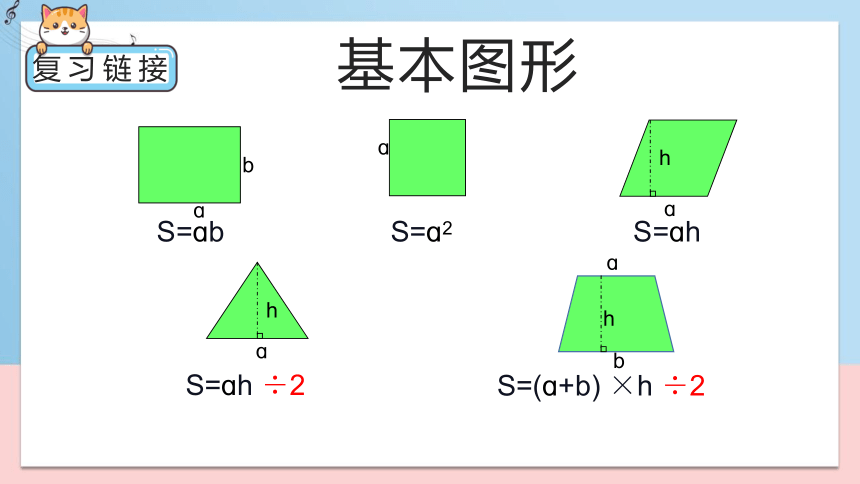
S=ɑh ÷2
S=(ɑ+b) ×h ÷2
S=ɑh
S=ɑb
S=ɑ2
h
ɑ
b
基本图形
复习链接
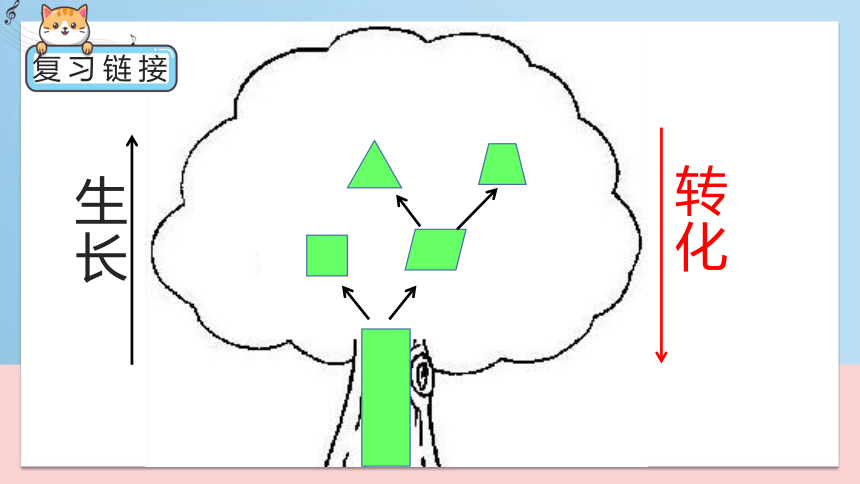
生长
转化
复习链接
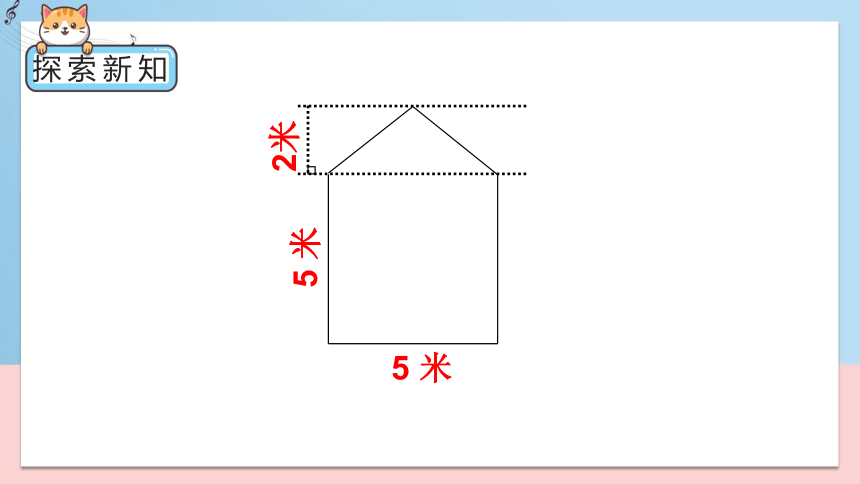
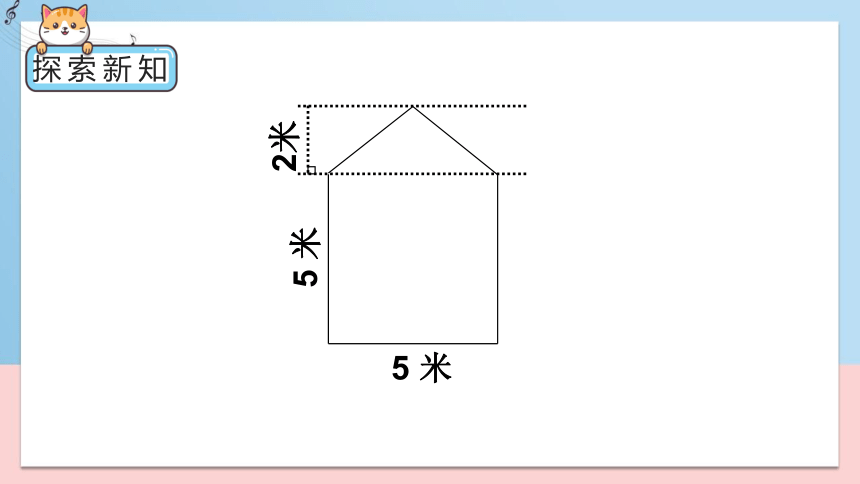
探索新知
组合图形
转化
5 米
5 米
2米
探索新知
合作要求:
1.议一议:讨论把组合图形转化成什么基本图形。
2.画一画:画出或剪出你们小组的思路。
5 米
5 米
2米
探索新知
分割法
三角形的面积+正方形的面积
两个梯形的面积
在组合图形内部添加辅助线,把组合图形分成几个基本图形,求面积之和。
分割求和
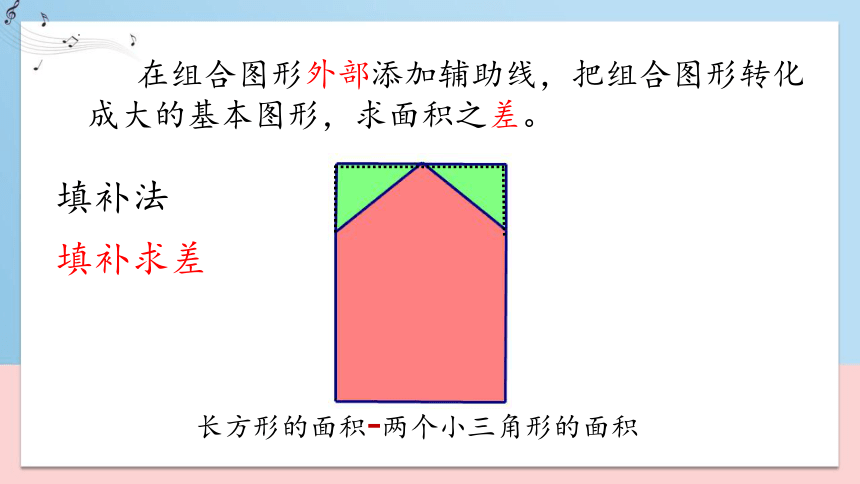
长方形的面积-两个小三角形的面积
在组合图形外部添加辅助线,把组合图形转化成大的基本图形,求面积之差。
填补法
填补求差
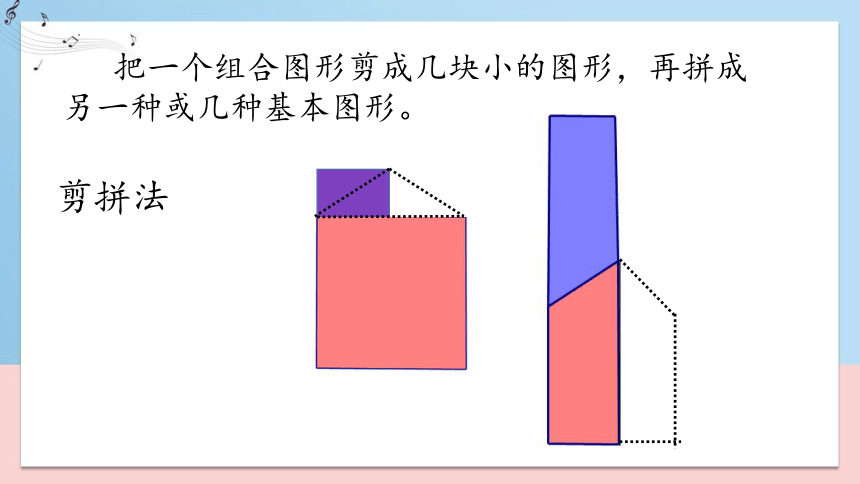
把一个组合图形剪成几块小的图形,再拼成另一种或几种基本图形。
剪拼法
5 米
5 米
2米
探索新知
5 米
5 米
2米
探索新知
三角形的面积+正方形的面积
正方形:5×5=25(平方米)
组合图形:5+25=30(平方米)
5
5
三角形:5×2÷2=5(平方米)
5
2
梯形的面积+梯形的面积
5
5÷2
两个梯形:(5+5+2)×(5÷2)÷2×2
5
2
=12×2.5
=4×2.5×3
=30(平方米)
5
5
2
5÷2
大长方形的面积-两个三角形的面积
两个三角形:5÷2×2÷2×2=5(平方米)
组合图形:35-5=30(平方米)
大长方形:(5+2)×5=35(平方米)
5÷2
5
一个大长方形的面积
大长方形:(5+2+5)×(5÷2)
5
2
=12×2.5
=30(平方米)
5
5
5÷2
2
小长方形的面积+正方形的面积
小长方形:5÷2×2=5(平方米)
组合图形:5+25=30(平方米)
正方形:5×5=25(平方米)
一个梯形的面积
5
5
5
(5+5+2)×5÷2
=12×5÷2
=30(平方米)
2
我国古代数学名著《九章算术》中记载了一些常见图形的面积计算方法。著名数学家刘徽在注文中用“以盈补虚”的方法加以说明。
以盈补虚(又称出入相补)是古数学中一条用于推证几何图形的面积或体积的基本原理。
其内容有四:
1.一个几何图形,可以切割成任意多块任何形状的小图形,总面积或体积维持不变=所有小图形面积或体积之和。
2.一个几何图形,可以任意旋转、倒置、移动、复制,面积或体积不变。
3.多个几何图形,可以任意拼合,总面积或总体积不变。
4.几何图形与其复制图形拼合,总面积或总体积加倍。
以盈补虚
5
5
1
1.求下面图形的面积(单位:cm)
练习巩固
12
8
8
4
正方形:8×8 =64(cm2)
S组合图形 = S正方形+S梯形
梯形:(8+12)×4÷2
=20×4÷2
=40(cm2)
组合图形:64+40=104(cm2)
(5+7)×8 - 8×7÷2
= 96 - 28
= 68(dm2)
S组合图形 = S长方形-S三角形
2.求下面图形的面积(单位:dm)
练习巩固
2.求下面图形的面积(单位:dm)
练习巩固
9
15
校园里有一块长方形草地,长15米,宽9米,中间有两条宽2米的小路,求草地的面积。
13
7
平移法
实践应用
生活中的组合图形
生活中的组合图形
生活中的组合图形
生活中的组合图形
组合图形
转化
基本图形
分割法
填补法
剪拼法
等积变形
根据图形和数据的特点选择合适的方法
平移法
回顾总结
生长
转化
……
拓展延伸
谢谢,再见
汇报人:小熊猫
汇报日期:2020.X.X
复习
ɑ
ɑ
b
ɑ
h
ɑ
h
S=ɑh ÷2
S=(ɑ+b) ×h ÷2
S=ɑh
S=ɑb
S=ɑ2
h
ɑ
b
基本图形
复习链接
生长
转化
复习链接
探索新知
组合图形
转化
5 米
5 米
2米
探索新知
合作要求:
1.议一议:讨论把组合图形转化成什么基本图形。
2.画一画:画出或剪出你们小组的思路。
5 米
5 米
2米
探索新知
分割法
三角形的面积+正方形的面积
两个梯形的面积
在组合图形内部添加辅助线,把组合图形分成几个基本图形,求面积之和。
分割求和
长方形的面积-两个小三角形的面积
在组合图形外部添加辅助线,把组合图形转化成大的基本图形,求面积之差。
填补法
填补求差
把一个组合图形剪成几块小的图形,再拼成另一种或几种基本图形。
剪拼法
5 米
5 米
2米
探索新知
5 米
5 米
2米
探索新知
三角形的面积+正方形的面积
正方形:5×5=25(平方米)
组合图形:5+25=30(平方米)
5
5
三角形:5×2÷2=5(平方米)
5
2
梯形的面积+梯形的面积
5
5÷2
两个梯形:(5+5+2)×(5÷2)÷2×2
5
2
=12×2.5
=4×2.5×3
=30(平方米)
5
5
2
5÷2
大长方形的面积-两个三角形的面积
两个三角形:5÷2×2÷2×2=5(平方米)
组合图形:35-5=30(平方米)
大长方形:(5+2)×5=35(平方米)
5÷2
5
一个大长方形的面积
大长方形:(5+2+5)×(5÷2)
5
2
=12×2.5
=30(平方米)
5
5
5÷2
2
小长方形的面积+正方形的面积
小长方形:5÷2×2=5(平方米)
组合图形:5+25=30(平方米)
正方形:5×5=25(平方米)
一个梯形的面积
5
5
5
(5+5+2)×5÷2
=12×5÷2
=30(平方米)
2
我国古代数学名著《九章算术》中记载了一些常见图形的面积计算方法。著名数学家刘徽在注文中用“以盈补虚”的方法加以说明。
以盈补虚(又称出入相补)是古数学中一条用于推证几何图形的面积或体积的基本原理。
其内容有四:
1.一个几何图形,可以切割成任意多块任何形状的小图形,总面积或体积维持不变=所有小图形面积或体积之和。
2.一个几何图形,可以任意旋转、倒置、移动、复制,面积或体积不变。
3.多个几何图形,可以任意拼合,总面积或总体积不变。
4.几何图形与其复制图形拼合,总面积或总体积加倍。
以盈补虚
5
5
1
1.求下面图形的面积(单位:cm)
练习巩固
12
8
8
4
正方形:8×8 =64(cm2)
S组合图形 = S正方形+S梯形
梯形:(8+12)×4÷2
=20×4÷2
=40(cm2)
组合图形:64+40=104(cm2)
(5+7)×8 - 8×7÷2
= 96 - 28
= 68(dm2)
S组合图形 = S长方形-S三角形
2.求下面图形的面积(单位:dm)
练习巩固
2.求下面图形的面积(单位:dm)
练习巩固
9
15
校园里有一块长方形草地,长15米,宽9米,中间有两条宽2米的小路,求草地的面积。
13
7
平移法
实践应用
生活中的组合图形
生活中的组合图形
生活中的组合图形
生活中的组合图形
组合图形
转化
基本图形
分割法
填补法
剪拼法
等积变形
根据图形和数据的特点选择合适的方法
平移法
回顾总结
生长
转化
……
拓展延伸
谢谢,再见
汇报人:小熊猫
汇报日期:2020.X.X
