3.3.2两点间的距离
图片预览






文档简介
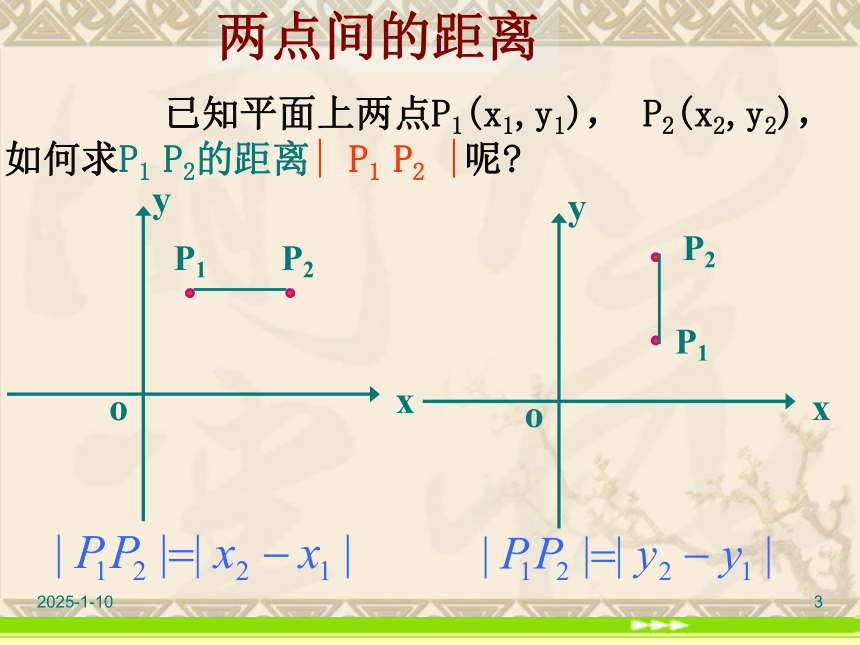
课件16张PPT。2019/2/213.3.2两点间的距离公式 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作2019/2/22问题提出 1.在平面直角坐标系中,根据直线的方程可以确定两直线平行、垂直等位置关系,以及求两相交直线的交点坐标,我们同样可以根据点的坐标确定点与点之间的相对位置关系. 2.平面上点与点之间的相对位置关系一般通过什么数量关系来反映?2019/2/23 已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢?两点间的距离2019/2/24 已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢?两点间的距离Q(x2,y1)2019/2/25(1) A(6,0), B(-2,0)
(2) C(0,-4), D(0,-1)
(3) P(6,0), Q(0,-2)
(4) M(2,1), N(5,-1)随堂练习1、求下列两点间的距离:2019/2/26例题分析解:设所求点为P(x,0),于是有解得x=1,所以所求点P(1,0)2019/2/272、求在x轴上与点A(5,12)的距离为13的坐标; 3、已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标。随堂练习2019/2/28例题分析例4、证明平行四边形四条边的平方和等于两条对角线的平方和。(b,c)(a+b,c)(a,0)(0,0)解:如图,以顶点A为坐标原点,AB所在直线为x轴,建立直角坐标系,则有A(0,0)设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)因此,平行四边形四条边的平方和等于两条对角线的 平方和2019/2/29第一步;建立坐标系,
用坐标系表示有关的量第二步:进行
有关代数运算第三步:把代数运算结果
“翻译”成几何关系用坐标法证明简单的平面几何问题的步骤:2019/2/210问题:初中我们证明过这样一个问题:
直角三角形斜边的中线长等于斜边的一半。你能用解析几何的方法证明此问题吗?2019/2/211证明:直角三角形斜边的中点到三个顶点的距离相等。(0,0)(a,0)(0,b)解:以顶点C为坐标原点,AC所在直线为x轴,建立直角坐标系,则有C(0,0)2019/2/212评注:本题是通过两点间的距离公式转化
为平面几何问题,运用对称法求出最小值。分析:本题可看作求在X轴上找一个点P到点M(4, 2)
与N(0,1)的距离和取得最小值。 2019/2/2131、平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是归纳总结2、坐标法证明简单平面几何问题的步骤第一步:建立坐标系,用坐标表示有关的量;第二步:进行有关的代数运算;第三步:把代数运算结果“翻译”所几何关系.2019/2/214布置作业:
P106练习:1,2.
P110习题3.3A组:6,7,8.2019/2/2154、求函数的 最小值提高训练2019/2/2165、直线l过点P(1,4),分别交x轴 的正方向和y轴的正方向于A、B两点.
(1).当︱PA︱. ︱PB︱最小时,求l的方程.
(2).当︱OA︱. ︱OB︱最小时,求l的方程.
高中数学老师欧阳文丰制作2019/2/22问题提出 1.在平面直角坐标系中,根据直线的方程可以确定两直线平行、垂直等位置关系,以及求两相交直线的交点坐标,我们同样可以根据点的坐标确定点与点之间的相对位置关系. 2.平面上点与点之间的相对位置关系一般通过什么数量关系来反映?2019/2/23 已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢?两点间的距离2019/2/24 已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢?两点间的距离Q(x2,y1)2019/2/25(1) A(6,0), B(-2,0)
(2) C(0,-4), D(0,-1)
(3) P(6,0), Q(0,-2)
(4) M(2,1), N(5,-1)随堂练习1、求下列两点间的距离:2019/2/26例题分析解:设所求点为P(x,0),于是有解得x=1,所以所求点P(1,0)2019/2/272、求在x轴上与点A(5,12)的距离为13的坐标; 3、已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标。随堂练习2019/2/28例题分析例4、证明平行四边形四条边的平方和等于两条对角线的平方和。(b,c)(a+b,c)(a,0)(0,0)解:如图,以顶点A为坐标原点,AB所在直线为x轴,建立直角坐标系,则有A(0,0)设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)因此,平行四边形四条边的平方和等于两条对角线的 平方和2019/2/29第一步;建立坐标系,
用坐标系表示有关的量第二步:进行
有关代数运算第三步:把代数运算结果
“翻译”成几何关系用坐标法证明简单的平面几何问题的步骤:2019/2/210问题:初中我们证明过这样一个问题:
直角三角形斜边的中线长等于斜边的一半。你能用解析几何的方法证明此问题吗?2019/2/211证明:直角三角形斜边的中点到三个顶点的距离相等。(0,0)(a,0)(0,b)解:以顶点C为坐标原点,AC所在直线为x轴,建立直角坐标系,则有C(0,0)2019/2/212评注:本题是通过两点间的距离公式转化
为平面几何问题,运用对称法求出最小值。分析:本题可看作求在X轴上找一个点P到点M(4, 2)
与N(0,1)的距离和取得最小值。 2019/2/2131、平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是归纳总结2、坐标法证明简单平面几何问题的步骤第一步:建立坐标系,用坐标表示有关的量;第二步:进行有关的代数运算;第三步:把代数运算结果“翻译”所几何关系.2019/2/214布置作业:
P106练习:1,2.
P110习题3.3A组:6,7,8.2019/2/2154、求函数的 最小值提高训练2019/2/2165、直线l过点P(1,4),分别交x轴 的正方向和y轴的正方向于A、B两点.
(1).当︱PA︱. ︱PB︱最小时,求l的方程.
(2).当︱OA︱. ︱OB︱最小时,求l的方程.
