苏科版七年级数学下册 7.5 多边形的内角和与外角和 教案
文档属性
| 名称 | 苏科版七年级数学下册 7.5 多边形的内角和与外角和 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 38.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 00:00:00 | ||
图片预览

文档简介
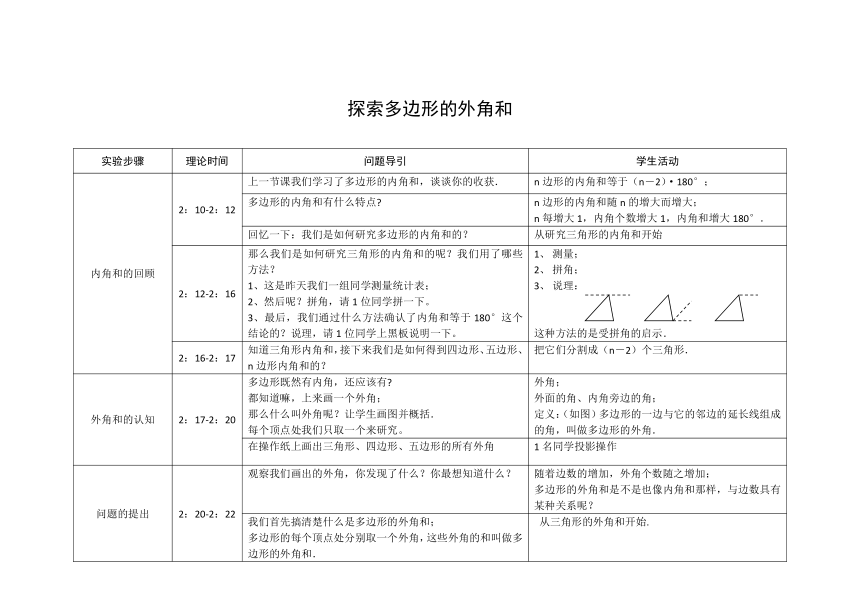
探索多边形的外角和
实验步骤 理论时间 问题导引 学生活动
内角和的回顾 2:10-2:12 上一节课我们学习了多边形的内角和,谈谈你的收获. n边形的内角和等于(n-2)·180°;
多边形的内角和有什么特点 n边形的内角和随n的增大而增大; n每增大1,内角个数增大1,内角和增大180°.
回忆一下:我们是如何研究多边形的内角和的? 从研究三角形的内角和开始
2:12-2:16 那么我们是如何研究三角形的内角和的呢?我们用了哪些方法? 1、这是昨天我们一组同学测量统计表; 2、然后呢?拼角,请1位同学拼一下。 3、最后,我们通过什么方法确认了内角和等于180°这个结论的?说理,请1位同学上黑板说明一下。 测量; 拼角; 说理: 这种方法的是受拼角的启示.
2:16-2:17 知道三角形内角和,接下来我们是如何得到四边形、五边形、n边形内角和的? 把它们分割成(n-2)个三角形.
外角和的认知 2:17-2:20 多边形既然有内角,还应该有 都知道嘛,上来画一个外角; 那么什么叫外角呢?让学生画图并概括. 每个顶点处我们只取一个来研究。 外角; 外面的角、内角旁边的角; 定义:(如图)多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
在操作纸上画出三角形、四边形、五边形的所有外角 1名同学投影操作
问题的提出 2:20-2:22 观察我们画出的外角,你发现了什么?你最想知道什么? 随着边数的增加,外角个数随之增加; 多边形的外角和是不是也像内角和那样,与边数具有某种关系呢?
我们首先搞清楚什么是多边形的外角和; 多边形的每个顶点处分别取一个外角,这些外角的和叫做多边形的外角和. 我们应该如何研究多边形的外角和呢? 从三角形的外角和开始.
探 索 活 动 测量 2:22-2:26 怎么研究三角形的外角和呢? 先用最简单的方法,测量你刚刚画出的三角形的外角和. 再任意画一个三角形,测量它的外角和.试试看! 测量展示:(2个学生,生讲师写) 图形∠1∠2∠3∠4∠5外角和三角形…………四边形……………五边形………………三角形…………
你发现了什么? 你有怎样的猜想? 我们发现:不论是三角形、四边形还是五边形,它们的外角和大致差不多,都在360°左右. 猜想:任意三角形、四边形还是五边形的外角和都是360°.
拼角 2:26-2:31 究竟是不是360°呢?如果是,那么当所有外角拼在一起时,就应该拼成一个______.请同学们利用附件5拼拼看! 借助附件5,拼角; 拼角展示:(2名同学配合展示拼角)
2:31-2:33 问:最后一个角能否既无缝隙又无重叠地拼进去? 动画演示五边形拼角过程(平移). 平移外角,只要让所在的边与相邻的外角平行或共线,那么既无缝隙又无重叠. 利用平行线的性质说明最后一个外角与空缺的角正好相等.
说理 2:33-2:38 通过测量、拼角,我们对三角形、四边形和五边形的外角和已有一个较为明确的认识;此时,你能确认任意n边形的外角和都等于360°吗? 不能:一是有误差,二是仅从有限个图形的操作并不能说明对任意 n边形都正确.
怎么办呢? 如何说理?(利用已有结论)请同学们思考,可以组内交流. 说理; 因为n边形每个顶点处的一个外角与内角之和为180°,每个外角等于180°减去与它共顶点的内角, 所以外角和=n·180°-内角和 = n·180°-(n-2)·180° =360°. 所以多边形的外角和与边数无关,都等于360°.
外 角 和 的 再 认 识 2:38-2:39 我们利用多边形的内角和得到了多边形的外角和的结论,这个结论可能出乎你的意料.其实我们还可以换一种方式来感受它的合理性.
转笔 2:39-2:43 刚才我们通过平移的方法把所有外角拼在一个点的周围,我们还可以通过旋转的方法. 转笔:笔转完一周,刚好转过了所有的外角. 明白:当所有角转完,最后笔停在哪里?
同学们仿照老师刚才的转笔方法,在《操作纸》上的三角形、四边形或五边形中转一转,体会其中的道理. 1、固定笔一端; 2、找准每次转动的起始位置和结束位置(建议用另一支笔画出来); 3、搞清每一次转过的是哪个角,理解两角相等的理由.
观察我们画出的射线,回忆三角形内角和的说理方法,你有什么想法? 说理的又一种方法;
活动经验的积累:拼角、转笔既是对猜想的验证,又是对新问题的探索,在直观感受中我们受到了理性的启发.
收缩 2:43-2:45 同学们再看一个有趣的图形收缩: 谈自己的想法. 当多边形逐渐收缩成一个点时,所有外角聚到同一点,构成一个周角.
拼角、转笔、收缩,异曲同工. 多边形外角和的本质揭示:可以拼成一个周角.
2:45-2:47 多边形的内角和与外角和,你更喜欢谁? 内角和随n的变化而变化,外角和与边数无关,很简明.
实验步骤 理论时间 问题导引 学生活动
内角和的回顾 2:10-2:12 上一节课我们学习了多边形的内角和,谈谈你的收获. n边形的内角和等于(n-2)·180°;
多边形的内角和有什么特点 n边形的内角和随n的增大而增大; n每增大1,内角个数增大1,内角和增大180°.
回忆一下:我们是如何研究多边形的内角和的? 从研究三角形的内角和开始
2:12-2:16 那么我们是如何研究三角形的内角和的呢?我们用了哪些方法? 1、这是昨天我们一组同学测量统计表; 2、然后呢?拼角,请1位同学拼一下。 3、最后,我们通过什么方法确认了内角和等于180°这个结论的?说理,请1位同学上黑板说明一下。 测量; 拼角; 说理: 这种方法的是受拼角的启示.
2:16-2:17 知道三角形内角和,接下来我们是如何得到四边形、五边形、n边形内角和的? 把它们分割成(n-2)个三角形.
外角和的认知 2:17-2:20 多边形既然有内角,还应该有 都知道嘛,上来画一个外角; 那么什么叫外角呢?让学生画图并概括. 每个顶点处我们只取一个来研究。 外角; 外面的角、内角旁边的角; 定义:(如图)多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
在操作纸上画出三角形、四边形、五边形的所有外角 1名同学投影操作
问题的提出 2:20-2:22 观察我们画出的外角,你发现了什么?你最想知道什么? 随着边数的增加,外角个数随之增加; 多边形的外角和是不是也像内角和那样,与边数具有某种关系呢?
我们首先搞清楚什么是多边形的外角和; 多边形的每个顶点处分别取一个外角,这些外角的和叫做多边形的外角和. 我们应该如何研究多边形的外角和呢? 从三角形的外角和开始.
探 索 活 动 测量 2:22-2:26 怎么研究三角形的外角和呢? 先用最简单的方法,测量你刚刚画出的三角形的外角和. 再任意画一个三角形,测量它的外角和.试试看! 测量展示:(2个学生,生讲师写) 图形∠1∠2∠3∠4∠5外角和三角形…………四边形……………五边形………………三角形…………
你发现了什么? 你有怎样的猜想? 我们发现:不论是三角形、四边形还是五边形,它们的外角和大致差不多,都在360°左右. 猜想:任意三角形、四边形还是五边形的外角和都是360°.
拼角 2:26-2:31 究竟是不是360°呢?如果是,那么当所有外角拼在一起时,就应该拼成一个______.请同学们利用附件5拼拼看! 借助附件5,拼角; 拼角展示:(2名同学配合展示拼角)
2:31-2:33 问:最后一个角能否既无缝隙又无重叠地拼进去? 动画演示五边形拼角过程(平移). 平移外角,只要让所在的边与相邻的外角平行或共线,那么既无缝隙又无重叠. 利用平行线的性质说明最后一个外角与空缺的角正好相等.
说理 2:33-2:38 通过测量、拼角,我们对三角形、四边形和五边形的外角和已有一个较为明确的认识;此时,你能确认任意n边形的外角和都等于360°吗? 不能:一是有误差,二是仅从有限个图形的操作并不能说明对任意 n边形都正确.
怎么办呢? 如何说理?(利用已有结论)请同学们思考,可以组内交流. 说理; 因为n边形每个顶点处的一个外角与内角之和为180°,每个外角等于180°减去与它共顶点的内角, 所以外角和=n·180°-内角和 = n·180°-(n-2)·180° =360°. 所以多边形的外角和与边数无关,都等于360°.
外 角 和 的 再 认 识 2:38-2:39 我们利用多边形的内角和得到了多边形的外角和的结论,这个结论可能出乎你的意料.其实我们还可以换一种方式来感受它的合理性.
转笔 2:39-2:43 刚才我们通过平移的方法把所有外角拼在一个点的周围,我们还可以通过旋转的方法. 转笔:笔转完一周,刚好转过了所有的外角. 明白:当所有角转完,最后笔停在哪里?
同学们仿照老师刚才的转笔方法,在《操作纸》上的三角形、四边形或五边形中转一转,体会其中的道理. 1、固定笔一端; 2、找准每次转动的起始位置和结束位置(建议用另一支笔画出来); 3、搞清每一次转过的是哪个角,理解两角相等的理由.
观察我们画出的射线,回忆三角形内角和的说理方法,你有什么想法? 说理的又一种方法;
活动经验的积累:拼角、转笔既是对猜想的验证,又是对新问题的探索,在直观感受中我们受到了理性的启发.
收缩 2:43-2:45 同学们再看一个有趣的图形收缩: 谈自己的想法. 当多边形逐渐收缩成一个点时,所有外角聚到同一点,构成一个周角.
拼角、转笔、收缩,异曲同工. 多边形外角和的本质揭示:可以拼成一个周角.
2:45-2:47 多边形的内角和与外角和,你更喜欢谁? 内角和随n的变化而变化,外角和与边数无关,很简明.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
