-第六章立体几何初步 单元检测卷 (word含解析)
文档属性
| 名称 | -第六章立体几何初步 单元检测卷 (word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 09:17:33 | ||
图片预览




文档简介
第六章立体几何初步单元检测卷
一、单选题
1.设,是两条不同的直线,,是两个不同的平面,则下列命题为真命题的是( )
A., B.,
C., D.,
2.如图,若斜边长为的等腰直角(与重合)是水平放置的的直观图,则的面积为( )
A.2 B. C. D.8
3.已知一个圆锥的体积为,其侧面积是底面积的2倍,则其底面半径为( )
A. B.3 C. D.
4.在如图所示的正方体中,M,N分别为棱BC和DD1的中点,则异面直线和B1M所成的角为( )
A.30° B.45° C.90° D.60°
5.某圆锥的母线长为3,侧面积为,则该圆锥的体积为( )
A. B. C. D.
6.已知是球面上的四个点,平面,,,则该球的表面积为( )
A. B. C. D.
7.已知为两条不同的直线,为两个不同的平面,则下列结论正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
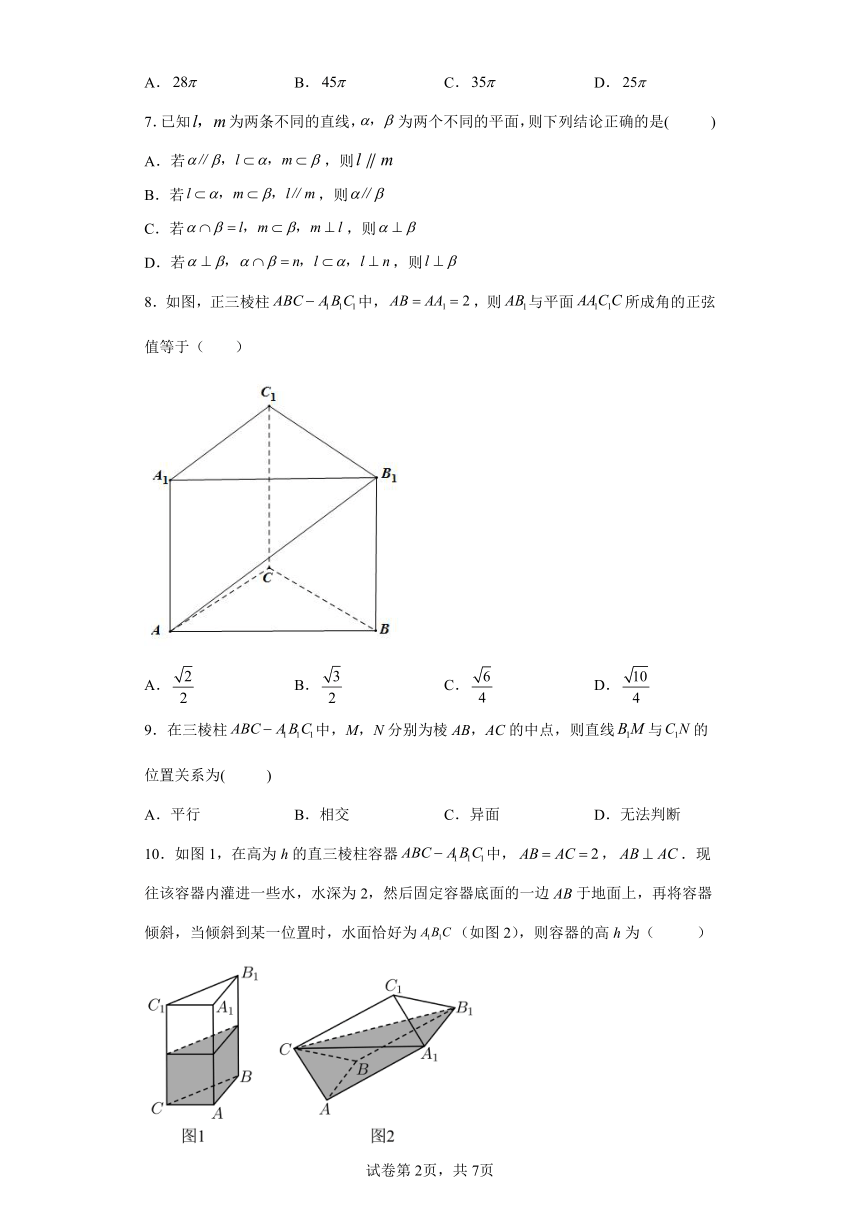
8.如图,正三棱柱中,,则与平面所成角的正弦值等于( )
A. B. C. D.
9.在三棱柱中,M,N分别为棱AB,AC的中点,则直线与的位置关系为( )
A.平行 B.相交 C.异面 D.无法判断
10.如图1,在高为h的直三棱柱容器中,,.现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为(如图2),则容器的高h为( )
A.3 B.4 C. D.6
11.如图,在正方形中,E,F分别是,的中点,G是的中点,现在沿,及将这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,则在这个空间图形中必有( )
A.平面 B.平面 C.平面 D.平面
12.已知几何体是正方体,则( )
A.平面 B.在直线上存在一点E,使得
C.平面 D.在直线上存在一点E,使得平面
二、填空题
13.已知圆柱的底面半径为,体积为4π,则该圆柱的侧面积为__________.
14.我国古代数学著作《九章算术.商功》阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.”彆臑是一类特殊的三棱锥,它的四个面都是直角三角形.如图,已知三棱锥是一个鳖臑,且平面ABC,,则___________.
15.如图,在三棱柱中,D,E,F分别是AB,AC,的中点.设三棱锥F-ADE的体积为,三棱柱的体积为,则=________.
16.18世纪英国数学家辛卜森运用定积分,推导出了现在中学数学教材中柱、锥、球、台等几何体的统一体积公式(其中L,N,M,h分别为的上底面面积、下底面面积、中截面面积和高),我们也称为“万能求积公式”.例如,已知球的半径为R,可得该球的体积为;已知正四棱锥的底面边长为a,高为h,可得该正四棱锥的体积为.类似地,运用该公式求解下列问题:如图,已知球O的表面积为,若用距离球心O都为2cm的两个平行平面去截球O,则夹在这两个平行平面之间的几何体的体积为______.
三、解答题
17.如图,在三棱柱中,点D是AB的中点.
(1)求证:∥平面.
(2)若平面ABC,,求证:平面.
18.如图,在底面是矩形的四棱锥中,底面,,分别是,的中点.
(1)若,求四棱锥的体积;
(2)求证:平面.
19.如图,是正方形,O是正方形的中心,底面,E是的中点.
(1)求证:∥平面;
(2)求证:面面.
20.如图,在多面体中,为等边三角形,,,,,F为EB的中点.
(1)证明:平面;
(2)求多面体的体积.
21.如图,在四棱锥中,面,,∥,AB=2AD=2CD.
(1)求证:;
(2)试问:线段上是否存在点,使得面,若存在,求出点的位置;若不存在,说明理由.
22.如图,四棱柱中,四边形为矩形,且平面平面ABCD,,,,M,E分别为,的中点.
(1)证明:平面;
(2)若,求点M到平面ADE的距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
由空间中线线,线面,面面间的位置关系判断即可.
【详解】
A:,,则无法判断n与的位置关系,A为假命题;
B:,,则无法判断n与的位置关系,B为假命题;
C:,,则m∥n或m与n是异面直线,C为假命题;
D:,,则n⊥β,D为真命题.
故选:D.
2.C
【解析】
【分析】
由斜二测还原图形计算即可求得结果.
【详解】
在斜二测直观图中, 由为等腰直角三角形,,可得,.
还原原图形如图:则,则
.
故选:C
3.C
【解析】
【分析】
根据圆锥的侧面展开图和圆锥体积公式以及侧面积公式,即可求出结果.
【详解】
设底面半径为,高为,母线为,如图所示:
则圆锥的体积,所以,即,
,则,
又,所以,故.
故选:C.
4.C
【解析】
【分析】
根据异面直线所成角的定义,找到与直线平行并且和相交的直线,即可找到异面直线所成的角,然后再求解即可.
【详解】
过点作交于,交于,易知,
所以,而,
所以,故,所以异面直线和B1M所成的角为.
故选:C
5.D
【解析】
【分析】
根据圆锥侧面积公式求出底面半径,进一步求出圆锥的高,再用公式求体积即可.
【详解】
设圆锥的母线长和底面半径分别为l,r,则,解得,
所以圆锥的高,则该圆锥的体积.
故选:D
6.B
【解析】
【分析】
根据可证三棱锥的三条侧棱两两互相垂直,将三棱锥补形成以为长宽高的长方体,又是球面上的四个点,所以球的直径为该长方体的体对角线,再根据题意可求出该长方体的体对角线长,进而求出球的表面积.
【详解】
由题意,作出三棱锥,如图所示,
因为平面,所以,又,所以,
又,所以平面;
同理平面,则两两互相垂直,
将三棱锥补形成以为长宽高的长方体,如下图所示,
又是球面上的四个点,所以球的直径为该长方体的体对角线,
又,,所以该长方体的体对角线长为,
即球的直径,其中是球的半径;
所以球的表面积为.
故选:B.
7.D
【解析】
【分析】
根据空间里面直线与平面、平面与平面位置关系的相关定理逐项判断即可.
【详解】
A,若,则或异面,故该选项错误;
B,若,则或相交,故该选项错误;
C,若,则α,β不一定垂直,故该选项错误;
D,若,则利用面面垂直的性质可得,故该选项正确.
故选:D.
8.C
【解析】
【分析】
取中点,连接,,证明平面,从而可得为与平面所成角,再利用三角函数计算的正弦值.
【详解】
取中点,连接,,在正三棱柱中,底面是正三角形,∴,又∵底面,∴,又,∴平面,∴为与平面所成角,由题意,,,在中,.
故选:C
9.B
【解析】
【分析】
作出图像,连接MN,由四边形是梯形是梯形即可判断.
【详解】
如图所示,连接MN,则MN∥BC且MN=BC,
又∵BC∥且BC=,∴MN∥且MN≠,
∴四边形是梯形,故与是梯形的两条腰,∴直线与相交.
故选:B.
10.A
【解析】
【分析】
利用两个图形装水的体积相等即可求解.
【详解】
在图1中,
在图2中,,
.
故选:A.
11.B
【解析】
【分析】
分析折叠前与折叠后位置关系、几何量的变与不变,可得、、三者相互垂直,根据线面垂直的判定定理,可判断与平面垂直.
【详解】
解:根据折叠前后不变,可得平面,故B正确;
因为过点只有一条直线与平面垂直,故A不正确;
因为,所以平面,又平面,
所以平面平面,过点作直线垂直于平面,该直线一定在平面 内,故C不正确;
因为不垂直于,所以平面不正确,故D不正确.
故选:B.
12.D
【解析】
【分析】
与平面相交,所以选项A错误;假设在直线上存在一点E,使得,找到矛盾,所以选项B错误;假设平面,找到矛盾,所以选项C错误;当E与重合时, 平面,所以选项D正确.
【详解】
由题得与平面相交,所以选项A错误;
假设在直线上存在一点E,使得,因为,所以,这不可能,所以选项B错误;
假设平面,则平面,所以平面,所以, 实际上,,所以平面不可能,所以选项C错误;
当E与重合时,因为平面,平面,所以平面,所以选项D正确.
故选:D
13.8π
【解析】
【分析】
根据条件先计算出母线长,再通过计算可求解.
【详解】
因为底面半径为,体积为,设母线为,则,得,
所以圆柱的侧面积为:,
故答案为:
14.
【解析】
【分析】
由题设易知,结合已知条件即可求的长度.
【详解】
由题设,△、△、△、△均为直角三角形,
又,
∴,,则,
∴.
故答案为:.
15.1∶24##
【解析】
【分析】
分别算出三棱锥F-ADE的与原三棱柱的底面积之比和高之比,进而根据椎体和柱体的体积公式求得答案.
【详解】
设三棱柱的底面ABC的面积为S,高为h,则其体积.
∵D,E分别为AB,AC的中点,∴的面积等于.
又∵F为的中点,∴F到底面ABC的距离是到底面ABC距离h的一半,即为.
∴于是三棱锥F-ADE的体积,则.
故答案为:.
16.
【解析】
【分析】
根据球的表面积公式求出球的半径,进而得出两个截面圆的半径,求出截面圆的面积,结合题意给的体积公式计算即可.
【详解】
由球O的表面积为,得球O的半径为3,
则两个截面圆和的半径都为,
根据对称性,几何体的中截面为圆O,其面积为;
所以几何体的体积为.
故答案为:.
17.(1)证明见解析;
(2)证明见解析.
【解析】
【分析】
(1)连接,交于点,连接,用中位线证明即可;
(2)证明CD⊥AB,CD⊥即可.
(1)
连接,交于点,连接
∵是三棱柱,∴四边形为平行四边形,∴是的中点.
∵点是的中点,∴是的中位线,∴,
又平面,平面,∴∥平面.
(2)
∵平面,平面,∴,
∵,,∴,
∵,平面,
∴平面.
18.(1)
(2)证明详见解析
【解析】
【分析】
(1)根据锥体的体积公式,即可求出结果;
(2)根据线面垂直的判定定理,即可证明面,又由中位线定理,可得,进而证明出结果.
(1)
解:∵在底面是矩形的四棱锥中,底面,,
∴;
(2)
证明:∵四边形为矩形,
∴,
∵底面,面,
∴,
又,∴面,
又,分别是,的中点,
∴,
∴平面.
19.(1)证明见解析
(2)证明见解析
【解析】
【分析】
(1)连接AC交BD于O,连接OE,由中位线即可得,得证;
(2)证明BD⊥平面PAC即可.
(1)
连接AC,交BD于O,连接OE,
在△CAP中,,∴,
又∵平面BDE,平面BDE,∴∥平面BDE;
(2)
∵PO⊥底面ABCD,则PO⊥BD,
又∵是正方形,则AC⊥BD,且,∴BD⊥平面PAC.
∵平面PBD,∴平面PAC⊥平面PBD.
20.(1)证明见详解
(2)
【解析】
【分析】
(1)作出辅助线,构造平行四边形,由线线平行得到线面平行;(2)先证明出面面垂直,进而作出四棱锥的高,求出底面积和高,利用锥体体积公式进行求解.
(1)
取EC中点M,连结DM,MF,因为F是EB的中点,所以MF∥BC,
∵ , ,∴四边形AFMD为平行四边形
∴∥.又平面,平面,∥平面.
(2)
∵,∴,
又∵,,∴平面,平面
∴平面平面,
过E作AB的垂线,垂足为H,
则EH为四棱锥的高.由题知.
底面四边形为直角梯形,其面积,
∴.
21.(1)证明见解析
(2)存在,点在线段上,靠近点的三等分点
【解析】
【分析】
(1)线面垂直得到线线垂直,作出辅助线证明线线垂直,可证明线面垂直;
(2)构造平行线,利用相似得到线线平行,进而得到线面平行,得到E点的位置.
(1)
∵面,面,
∴,
取AB的中点F,连接CF,因为,,AB=2AD=2CD,
所以AF=CD,故四边形ADCF为正方形,所以CF⊥AB,,又CF=BF,所以,从而,
又,
∴面,又面,∴;
(2)
存在点,在线段上,靠近点的三等分点,即,
证明如下:连接,交于,再连接,
∵,△DOC∽,∴,
又,
∴,面,面,
∴面.
22.(1)证明见解析
(2)
【解析】
【分析】
(1)分别取AD和BC的中点H,P,连接MH,HP,PE,即可得到,,从而得到四边形为平行四边形,则,又,所以,即可得证.
(2)由面面垂直的性质得到平面,则,再由得到平面,从而得到平面,最后根据利用等体积法求出点到平面的距离;
(1)
证明:如图,
分别取AD和BC的中点H,P,连接MH,HP,PE,
则,,,,
所以,,
所以四边形为平行四边形,
所以,又.所以.
因为平面,平面,
所以平面.
(2)
解:因为四边形为矩形,所以,
因为平面平面ABCD,平面平面,
所以平面ABCD,平面ABCD,所以,
因为,,所以,,平面,所以平面,
因为,所以平面
.
因为,,所以平面MHPE,所以,
故
设点M到平面ADE的距离为d,
则,
解得.
所以点M到平面ADE的距离为.
答案第1页,共2页
一、单选题
1.设,是两条不同的直线,,是两个不同的平面,则下列命题为真命题的是( )
A., B.,
C., D.,
2.如图,若斜边长为的等腰直角(与重合)是水平放置的的直观图,则的面积为( )
A.2 B. C. D.8
3.已知一个圆锥的体积为,其侧面积是底面积的2倍,则其底面半径为( )
A. B.3 C. D.
4.在如图所示的正方体中,M,N分别为棱BC和DD1的中点,则异面直线和B1M所成的角为( )
A.30° B.45° C.90° D.60°
5.某圆锥的母线长为3,侧面积为,则该圆锥的体积为( )
A. B. C. D.
6.已知是球面上的四个点,平面,,,则该球的表面积为( )
A. B. C. D.
7.已知为两条不同的直线,为两个不同的平面,则下列结论正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
8.如图,正三棱柱中,,则与平面所成角的正弦值等于( )
A. B. C. D.
9.在三棱柱中,M,N分别为棱AB,AC的中点,则直线与的位置关系为( )
A.平行 B.相交 C.异面 D.无法判断
10.如图1,在高为h的直三棱柱容器中,,.现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为(如图2),则容器的高h为( )
A.3 B.4 C. D.6
11.如图,在正方形中,E,F分别是,的中点,G是的中点,现在沿,及将这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,则在这个空间图形中必有( )
A.平面 B.平面 C.平面 D.平面
12.已知几何体是正方体,则( )
A.平面 B.在直线上存在一点E,使得
C.平面 D.在直线上存在一点E,使得平面
二、填空题
13.已知圆柱的底面半径为,体积为4π,则该圆柱的侧面积为__________.
14.我国古代数学著作《九章算术.商功》阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.”彆臑是一类特殊的三棱锥,它的四个面都是直角三角形.如图,已知三棱锥是一个鳖臑,且平面ABC,,则___________.
15.如图,在三棱柱中,D,E,F分别是AB,AC,的中点.设三棱锥F-ADE的体积为,三棱柱的体积为,则=________.
16.18世纪英国数学家辛卜森运用定积分,推导出了现在中学数学教材中柱、锥、球、台等几何体的统一体积公式(其中L,N,M,h分别为的上底面面积、下底面面积、中截面面积和高),我们也称为“万能求积公式”.例如,已知球的半径为R,可得该球的体积为;已知正四棱锥的底面边长为a,高为h,可得该正四棱锥的体积为.类似地,运用该公式求解下列问题:如图,已知球O的表面积为,若用距离球心O都为2cm的两个平行平面去截球O,则夹在这两个平行平面之间的几何体的体积为______.
三、解答题
17.如图,在三棱柱中,点D是AB的中点.
(1)求证:∥平面.
(2)若平面ABC,,求证:平面.
18.如图,在底面是矩形的四棱锥中,底面,,分别是,的中点.
(1)若,求四棱锥的体积;
(2)求证:平面.
19.如图,是正方形,O是正方形的中心,底面,E是的中点.
(1)求证:∥平面;
(2)求证:面面.
20.如图,在多面体中,为等边三角形,,,,,F为EB的中点.
(1)证明:平面;
(2)求多面体的体积.
21.如图,在四棱锥中,面,,∥,AB=2AD=2CD.
(1)求证:;
(2)试问:线段上是否存在点,使得面,若存在,求出点的位置;若不存在,说明理由.
22.如图,四棱柱中,四边形为矩形,且平面平面ABCD,,,,M,E分别为,的中点.
(1)证明:平面;
(2)若,求点M到平面ADE的距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
由空间中线线,线面,面面间的位置关系判断即可.
【详解】
A:,,则无法判断n与的位置关系,A为假命题;
B:,,则无法判断n与的位置关系,B为假命题;
C:,,则m∥n或m与n是异面直线,C为假命题;
D:,,则n⊥β,D为真命题.
故选:D.
2.C
【解析】
【分析】
由斜二测还原图形计算即可求得结果.
【详解】
在斜二测直观图中, 由为等腰直角三角形,,可得,.
还原原图形如图:则,则
.
故选:C
3.C
【解析】
【分析】
根据圆锥的侧面展开图和圆锥体积公式以及侧面积公式,即可求出结果.
【详解】
设底面半径为,高为,母线为,如图所示:
则圆锥的体积,所以,即,
,则,
又,所以,故.
故选:C.
4.C
【解析】
【分析】
根据异面直线所成角的定义,找到与直线平行并且和相交的直线,即可找到异面直线所成的角,然后再求解即可.
【详解】
过点作交于,交于,易知,
所以,而,
所以,故,所以异面直线和B1M所成的角为.
故选:C
5.D
【解析】
【分析】
根据圆锥侧面积公式求出底面半径,进一步求出圆锥的高,再用公式求体积即可.
【详解】
设圆锥的母线长和底面半径分别为l,r,则,解得,
所以圆锥的高,则该圆锥的体积.
故选:D
6.B
【解析】
【分析】
根据可证三棱锥的三条侧棱两两互相垂直,将三棱锥补形成以为长宽高的长方体,又是球面上的四个点,所以球的直径为该长方体的体对角线,再根据题意可求出该长方体的体对角线长,进而求出球的表面积.
【详解】
由题意,作出三棱锥,如图所示,
因为平面,所以,又,所以,
又,所以平面;
同理平面,则两两互相垂直,
将三棱锥补形成以为长宽高的长方体,如下图所示,
又是球面上的四个点,所以球的直径为该长方体的体对角线,
又,,所以该长方体的体对角线长为,
即球的直径,其中是球的半径;
所以球的表面积为.
故选:B.
7.D
【解析】
【分析】
根据空间里面直线与平面、平面与平面位置关系的相关定理逐项判断即可.
【详解】
A,若,则或异面,故该选项错误;
B,若,则或相交,故该选项错误;
C,若,则α,β不一定垂直,故该选项错误;
D,若,则利用面面垂直的性质可得,故该选项正确.
故选:D.
8.C
【解析】
【分析】
取中点,连接,,证明平面,从而可得为与平面所成角,再利用三角函数计算的正弦值.
【详解】
取中点,连接,,在正三棱柱中,底面是正三角形,∴,又∵底面,∴,又,∴平面,∴为与平面所成角,由题意,,,在中,.
故选:C
9.B
【解析】
【分析】
作出图像,连接MN,由四边形是梯形是梯形即可判断.
【详解】
如图所示,连接MN,则MN∥BC且MN=BC,
又∵BC∥且BC=,∴MN∥且MN≠,
∴四边形是梯形,故与是梯形的两条腰,∴直线与相交.
故选:B.
10.A
【解析】
【分析】
利用两个图形装水的体积相等即可求解.
【详解】
在图1中,
在图2中,,
.
故选:A.
11.B
【解析】
【分析】
分析折叠前与折叠后位置关系、几何量的变与不变,可得、、三者相互垂直,根据线面垂直的判定定理,可判断与平面垂直.
【详解】
解:根据折叠前后不变,可得平面,故B正确;
因为过点只有一条直线与平面垂直,故A不正确;
因为,所以平面,又平面,
所以平面平面,过点作直线垂直于平面,该直线一定在平面 内,故C不正确;
因为不垂直于,所以平面不正确,故D不正确.
故选:B.
12.D
【解析】
【分析】
与平面相交,所以选项A错误;假设在直线上存在一点E,使得,找到矛盾,所以选项B错误;假设平面,找到矛盾,所以选项C错误;当E与重合时, 平面,所以选项D正确.
【详解】
由题得与平面相交,所以选项A错误;
假设在直线上存在一点E,使得,因为,所以,这不可能,所以选项B错误;
假设平面,则平面,所以平面,所以, 实际上,,所以平面不可能,所以选项C错误;
当E与重合时,因为平面,平面,所以平面,所以选项D正确.
故选:D
13.8π
【解析】
【分析】
根据条件先计算出母线长,再通过计算可求解.
【详解】
因为底面半径为,体积为,设母线为,则,得,
所以圆柱的侧面积为:,
故答案为:
14.
【解析】
【分析】
由题设易知,结合已知条件即可求的长度.
【详解】
由题设,△、△、△、△均为直角三角形,
又,
∴,,则,
∴.
故答案为:.
15.1∶24##
【解析】
【分析】
分别算出三棱锥F-ADE的与原三棱柱的底面积之比和高之比,进而根据椎体和柱体的体积公式求得答案.
【详解】
设三棱柱的底面ABC的面积为S,高为h,则其体积.
∵D,E分别为AB,AC的中点,∴的面积等于.
又∵F为的中点,∴F到底面ABC的距离是到底面ABC距离h的一半,即为.
∴于是三棱锥F-ADE的体积,则.
故答案为:.
16.
【解析】
【分析】
根据球的表面积公式求出球的半径,进而得出两个截面圆的半径,求出截面圆的面积,结合题意给的体积公式计算即可.
【详解】
由球O的表面积为,得球O的半径为3,
则两个截面圆和的半径都为,
根据对称性,几何体的中截面为圆O,其面积为;
所以几何体的体积为.
故答案为:.
17.(1)证明见解析;
(2)证明见解析.
【解析】
【分析】
(1)连接,交于点,连接,用中位线证明即可;
(2)证明CD⊥AB,CD⊥即可.
(1)
连接,交于点,连接
∵是三棱柱,∴四边形为平行四边形,∴是的中点.
∵点是的中点,∴是的中位线,∴,
又平面,平面,∴∥平面.
(2)
∵平面,平面,∴,
∵,,∴,
∵,平面,
∴平面.
18.(1)
(2)证明详见解析
【解析】
【分析】
(1)根据锥体的体积公式,即可求出结果;
(2)根据线面垂直的判定定理,即可证明面,又由中位线定理,可得,进而证明出结果.
(1)
解:∵在底面是矩形的四棱锥中,底面,,
∴;
(2)
证明:∵四边形为矩形,
∴,
∵底面,面,
∴,
又,∴面,
又,分别是,的中点,
∴,
∴平面.
19.(1)证明见解析
(2)证明见解析
【解析】
【分析】
(1)连接AC交BD于O,连接OE,由中位线即可得,得证;
(2)证明BD⊥平面PAC即可.
(1)
连接AC,交BD于O,连接OE,
在△CAP中,,∴,
又∵平面BDE,平面BDE,∴∥平面BDE;
(2)
∵PO⊥底面ABCD,则PO⊥BD,
又∵是正方形,则AC⊥BD,且,∴BD⊥平面PAC.
∵平面PBD,∴平面PAC⊥平面PBD.
20.(1)证明见详解
(2)
【解析】
【分析】
(1)作出辅助线,构造平行四边形,由线线平行得到线面平行;(2)先证明出面面垂直,进而作出四棱锥的高,求出底面积和高,利用锥体体积公式进行求解.
(1)
取EC中点M,连结DM,MF,因为F是EB的中点,所以MF∥BC,
∵ , ,∴四边形AFMD为平行四边形
∴∥.又平面,平面,∥平面.
(2)
∵,∴,
又∵,,∴平面,平面
∴平面平面,
过E作AB的垂线,垂足为H,
则EH为四棱锥的高.由题知.
底面四边形为直角梯形,其面积,
∴.
21.(1)证明见解析
(2)存在,点在线段上,靠近点的三等分点
【解析】
【分析】
(1)线面垂直得到线线垂直,作出辅助线证明线线垂直,可证明线面垂直;
(2)构造平行线,利用相似得到线线平行,进而得到线面平行,得到E点的位置.
(1)
∵面,面,
∴,
取AB的中点F,连接CF,因为,,AB=2AD=2CD,
所以AF=CD,故四边形ADCF为正方形,所以CF⊥AB,,又CF=BF,所以,从而,
又,
∴面,又面,∴;
(2)
存在点,在线段上,靠近点的三等分点,即,
证明如下:连接,交于,再连接,
∵,△DOC∽,∴,
又,
∴,面,面,
∴面.
22.(1)证明见解析
(2)
【解析】
【分析】
(1)分别取AD和BC的中点H,P,连接MH,HP,PE,即可得到,,从而得到四边形为平行四边形,则,又,所以,即可得证.
(2)由面面垂直的性质得到平面,则,再由得到平面,从而得到平面,最后根据利用等体积法求出点到平面的距离;
(1)
证明:如图,
分别取AD和BC的中点H,P,连接MH,HP,PE,
则,,,,
所以,,
所以四边形为平行四边形,
所以,又.所以.
因为平面,平面,
所以平面.
(2)
解:因为四边形为矩形,所以,
因为平面平面ABCD,平面平面,
所以平面ABCD,平面ABCD,所以,
因为,,所以,,平面,所以平面,
因为,所以平面
.
因为,,所以平面MHPE,所以,
故
设点M到平面ADE的距离为d,
则,
解得.
所以点M到平面ADE的距离为.
答案第1页,共2页
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
