青岛版小学六年级数学上册《解决两种量之间的关系的分数乘法问题》教学建议
文档属性
| 名称 | 青岛版小学六年级数学上册《解决两种量之间的关系的分数乘法问题》教学建议 |

|
|
| 格式 | doc | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 00:00:00 | ||
图片预览

文档简介
《解决两种量之间的关系的分数乘法问题》教学建议
信息窗3——北京人
本信息窗呈现的是“北京人”头像和山洞的情境,图中包含的主要信息是:“北京人”成年女子平均身高只有144厘米,现代成年女子平均身高比“北京人”女子高;“北京人”的脑容量比现代人的脑容量少,现代人平均脑容量是1400毫升。借助问题“现代成年女子平均身高是多少厘米”、“‘北京人’平均脑容量是多少毫升”,引入对稍复杂的分数乘法问题(两种量之间的关系)的学习。
通过本信息窗的学习,学生应结合具体情境,在解决问题的过程中展开对稍复杂的分数乘法问题(两个量之间的关系)的学习,帮助学生学会画线段图分析分数乘法两步问题,同时加强分数乘加混合运算的学习。
教学时,教师可以承接第二个信息窗的内容,继续引入了解我国的世界遗产“北京人”,先让学生对信息窗内容进行独立阅读,激起学生学习兴趣的同时有序梳理信息,并根据信息有针对性地提出数学问题,展开对a×(1+)数乘法问题的学习。
“合作探索”中有1个红点问题和1个绿点问题。红点问题是进一步学习稍复杂的分数乘法问题,它反映的是两个量之间的数量关系。绿点问题是在红点问题的基础上对分数乘法问题的学习。
红点标示的问题是:“现代成年女子平均身高是多少厘米?”教材呈现了两种不同的解题思路和线段图,引入对稍复杂的分数乘加问题和运算顺序的学习。
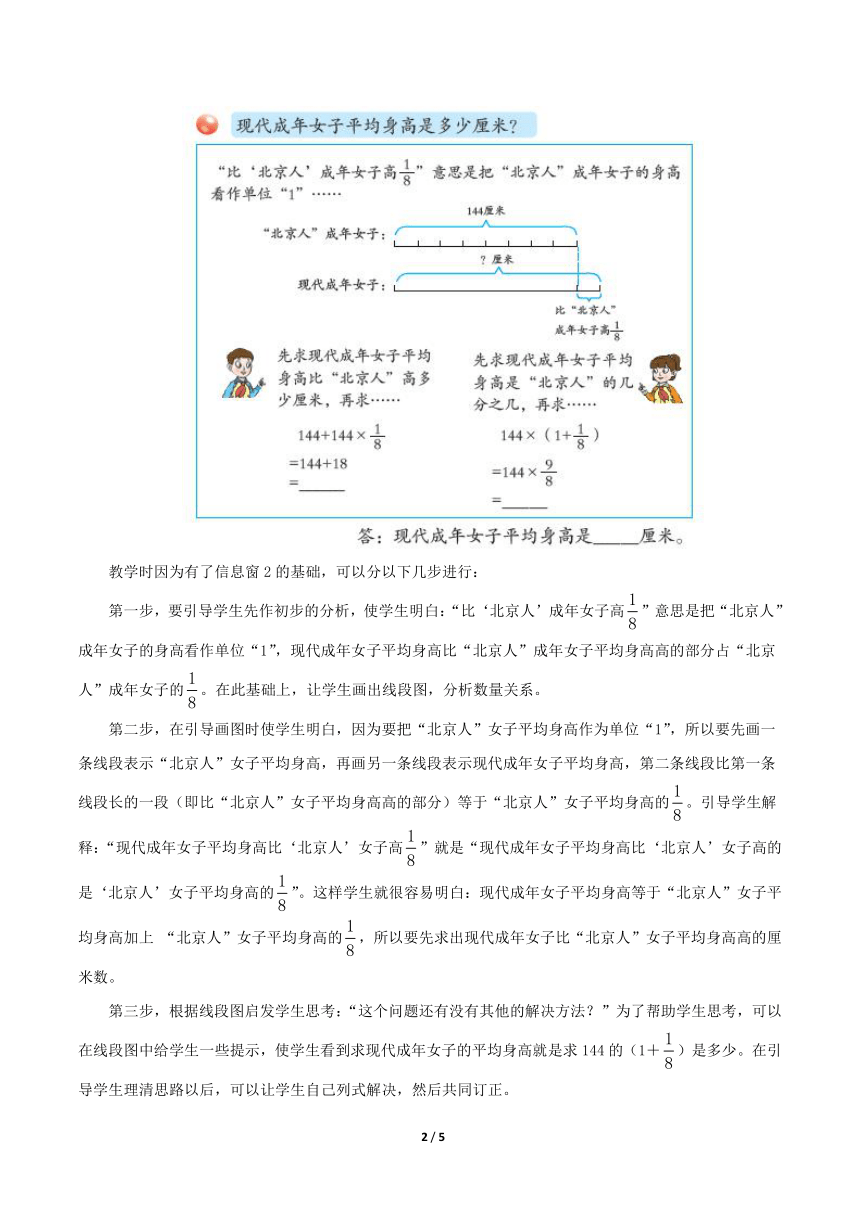
教学时因为有了信息窗2的基础,可以分以下几步进行:
第一步,要引导学生先作初步的分析,使学生明白:“比‘北京人’成年女子高”意思是把“北京人”成年女子的身高看作单位“1”,现代成年女子平均身高比“北京人”成年女子平均身高高的部分占“北京人”成年女子的。在此基础上,让学生画出线段图,分析数量关系。
第二步,在引导画图时使学生明白,因为要把“北京人”女子平均身高作为单位“1”,所以要先画一条线段表示“北京人”女子平均身高,再画另一条线段表示现代成年女子平均身高,第二条线段比第一条线段长的一段(即比“北京人”女子平均身高高的部分)等于“北京人”女子平均身高的。引导学生解释:“现代成年女子平均身高比‘北京人’女子高”就是“现代成年女子平均身高比‘北京人’女子高的是‘北京人’女子平均身高的”。这样学生就很容易明白:现代成年女子平均身高等于“北京人”女子平均身高加上 “北京人”女子平均身高的,所以要先求出现代成年女子比“北京人”女子平均身高高的厘米数。
第三步,根据线段图启发学生思考:“这个问题还有没有其他的解决方法?”为了帮助学生思考,可以在线段图中给学生一些提示,使学生看到求现代成年女子的平均身高就是求144的(1+)是多少。在引导学生理清思路以后,可以让学生自己列式解决,然后共同订正。
第四步,对比上述两种解法,通过讨论,启发学生选择自己喜欢的解题策略。
绿点标示的问题是:“‘北京人’平均脑容量是多少毫升?”教材呈现了线段图和思路分析及算式,引入对稍复杂的分数乘减问题和运算顺序的学习。
教学时,可以启发学生用自己喜欢的策略解答问题,然后给学生充分的组内交流的时间和空间,最后组间交流解决问题的不同策略和想法。
“自主练习”第1题是一道填空题。练习时,可以先让学生独立完成,然后充分交流关键句的意义,理解关键句的意义并订正结果。可以借助线段图帮助学生掌握这一基本内容。
第2题是对应红点知识的基本练习题。练习时,先让学生独立理解题意、解决问题,然后组内借助线段图进行交流,最后组间交流不同的解题思路,沟通解题思路之间的联系,帮助学生加强理解。本题还渗透了植树造林保护环境的意识。
第3题是对应绿点知识的基本练习。练习时,先让学生独立解答,交流时重点让学生沟通解题思路。
第4题巩固运算律的计算题。练习时,让学生独立完成。订正、交流时,重点引导学生学会分析数据特点,灵活运用运算律。
第5、6、7题是用已学知识解决实际问题的练习题。练习时,先让学生独立解答,交流时重点让学生沟通解题思路。第5、6题可以放手让同桌交流解题思路,帮助学习有困难的学生巩固知识。第7题可以在学生独立解决完后,直接在全班交流解题思路,反馈学生的掌握情况。也可以将这三道题作为课堂作业,让学生独立完成后老师批改了解学生的掌握情况。本题让学生进一步了解世界文化遗产。
4 / 5
信息窗3——北京人
本信息窗呈现的是“北京人”头像和山洞的情境,图中包含的主要信息是:“北京人”成年女子平均身高只有144厘米,现代成年女子平均身高比“北京人”女子高;“北京人”的脑容量比现代人的脑容量少,现代人平均脑容量是1400毫升。借助问题“现代成年女子平均身高是多少厘米”、“‘北京人’平均脑容量是多少毫升”,引入对稍复杂的分数乘法问题(两种量之间的关系)的学习。
通过本信息窗的学习,学生应结合具体情境,在解决问题的过程中展开对稍复杂的分数乘法问题(两个量之间的关系)的学习,帮助学生学会画线段图分析分数乘法两步问题,同时加强分数乘加混合运算的学习。
教学时,教师可以承接第二个信息窗的内容,继续引入了解我国的世界遗产“北京人”,先让学生对信息窗内容进行独立阅读,激起学生学习兴趣的同时有序梳理信息,并根据信息有针对性地提出数学问题,展开对a×(1+)数乘法问题的学习。
“合作探索”中有1个红点问题和1个绿点问题。红点问题是进一步学习稍复杂的分数乘法问题,它反映的是两个量之间的数量关系。绿点问题是在红点问题的基础上对分数乘法问题的学习。
红点标示的问题是:“现代成年女子平均身高是多少厘米?”教材呈现了两种不同的解题思路和线段图,引入对稍复杂的分数乘加问题和运算顺序的学习。
教学时因为有了信息窗2的基础,可以分以下几步进行:
第一步,要引导学生先作初步的分析,使学生明白:“比‘北京人’成年女子高”意思是把“北京人”成年女子的身高看作单位“1”,现代成年女子平均身高比“北京人”成年女子平均身高高的部分占“北京人”成年女子的。在此基础上,让学生画出线段图,分析数量关系。
第二步,在引导画图时使学生明白,因为要把“北京人”女子平均身高作为单位“1”,所以要先画一条线段表示“北京人”女子平均身高,再画另一条线段表示现代成年女子平均身高,第二条线段比第一条线段长的一段(即比“北京人”女子平均身高高的部分)等于“北京人”女子平均身高的。引导学生解释:“现代成年女子平均身高比‘北京人’女子高”就是“现代成年女子平均身高比‘北京人’女子高的是‘北京人’女子平均身高的”。这样学生就很容易明白:现代成年女子平均身高等于“北京人”女子平均身高加上 “北京人”女子平均身高的,所以要先求出现代成年女子比“北京人”女子平均身高高的厘米数。
第三步,根据线段图启发学生思考:“这个问题还有没有其他的解决方法?”为了帮助学生思考,可以在线段图中给学生一些提示,使学生看到求现代成年女子的平均身高就是求144的(1+)是多少。在引导学生理清思路以后,可以让学生自己列式解决,然后共同订正。
第四步,对比上述两种解法,通过讨论,启发学生选择自己喜欢的解题策略。
绿点标示的问题是:“‘北京人’平均脑容量是多少毫升?”教材呈现了线段图和思路分析及算式,引入对稍复杂的分数乘减问题和运算顺序的学习。
教学时,可以启发学生用自己喜欢的策略解答问题,然后给学生充分的组内交流的时间和空间,最后组间交流解决问题的不同策略和想法。
“自主练习”第1题是一道填空题。练习时,可以先让学生独立完成,然后充分交流关键句的意义,理解关键句的意义并订正结果。可以借助线段图帮助学生掌握这一基本内容。
第2题是对应红点知识的基本练习题。练习时,先让学生独立理解题意、解决问题,然后组内借助线段图进行交流,最后组间交流不同的解题思路,沟通解题思路之间的联系,帮助学生加强理解。本题还渗透了植树造林保护环境的意识。
第3题是对应绿点知识的基本练习。练习时,先让学生独立解答,交流时重点让学生沟通解题思路。
第4题巩固运算律的计算题。练习时,让学生独立完成。订正、交流时,重点引导学生学会分析数据特点,灵活运用运算律。
第5、6、7题是用已学知识解决实际问题的练习题。练习时,先让学生独立解答,交流时重点让学生沟通解题思路。第5、6题可以放手让同桌交流解题思路,帮助学习有困难的学生巩固知识。第7题可以在学生独立解决完后,直接在全班交流解题思路,反馈学生的掌握情况。也可以将这三道题作为课堂作业,让学生独立完成后老师批改了解学生的掌握情况。本题让学生进一步了解世界文化遗产。
4 / 5
