广东省深圳市罗湖区2021-2022学年九年级下学期 寒假作业检查(开学考)数学试题(含答案)
文档属性
| 名称 | 广东省深圳市罗湖区2021-2022学年九年级下学期 寒假作业检查(开学考)数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 329.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 17:47:41 | ||
图片预览


文档简介
(
2
) (
+
) (
200
200
) (
.
) (
D
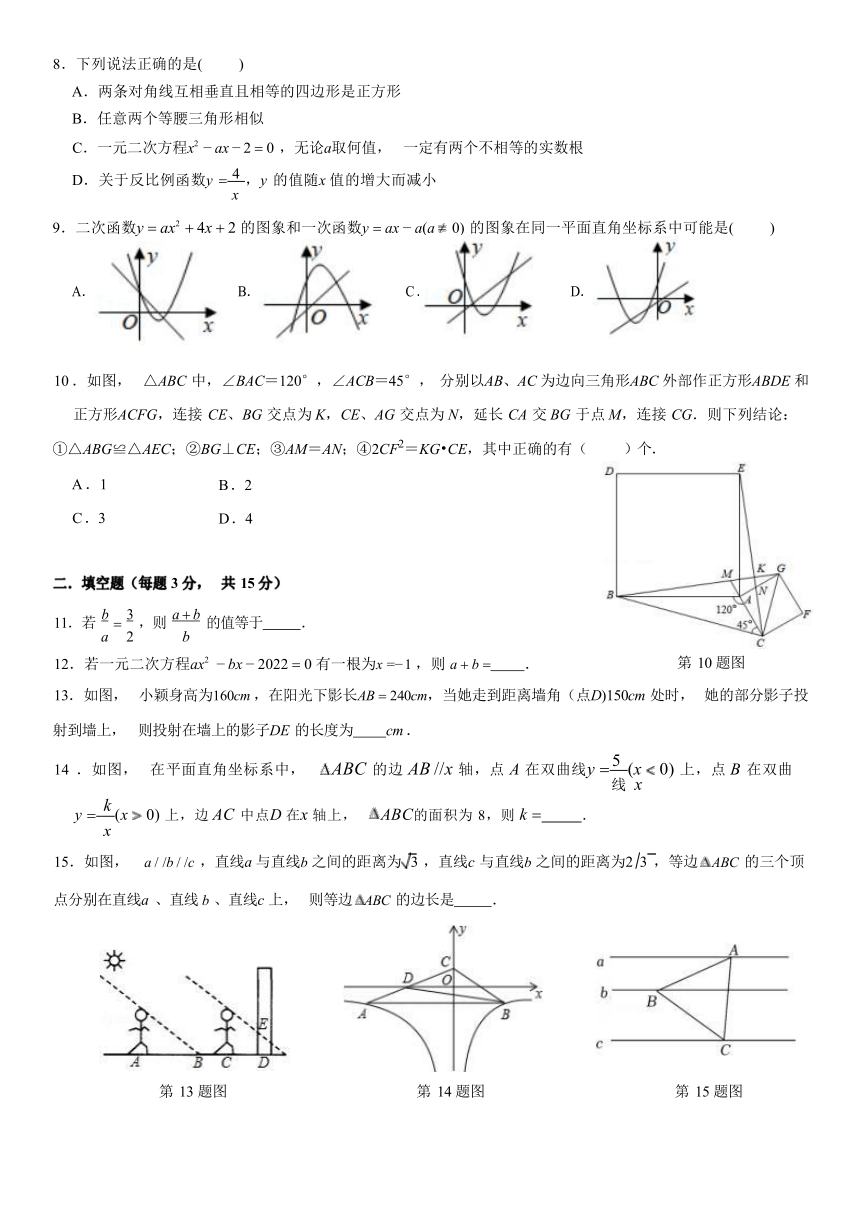
)2021—2022 学年度第二学期寒假作业检查 初三年级数学试卷 3.5
说明:
1. 答题前,务必将自己的姓名、学号等填写在答题卷规定的位置上.
2. 考生必须在答题卷上按规定作答,凡在试卷、草稿纸上作答的,其答案一律无效.
3. 全卷共 4 页,考试时间 90 分钟, 满分 100 分.
一.单选题(每题 3 分, 共 30 分)
1.如图, 该几何体的左视图是( )
A . B . C.
2.在一个不透明的袋子里装有红球、黄球共 20 个, 这些球除颜色外都相同. 小明通过多次试验发现, 摸出红球的 频率稳定在 0.25 左右, 则袋子中红球的个数最有可能是( )
A .5 B .10 C .12 D .15
3.将抛物线y x2 2x 3向左平移 2 个单位, 再向上平移 1 个单位, 得到的抛物线的解析式为( )
A. y (x 3)2 4 B. y (x 1)2 4 C .y (x 1)2 3 D. y (x 1)2 2
4.如图, 在菱形ABCD 中, A 60 ,AB 2 ,点 M 为边AD 的中点, 连接BD 交 CM 于点N ,则 BN 的长是( )
4
A . 1 B . 3
C . D . 3
5.如图, 学校课外生物小组的试验园地的形状是长 35 米、宽 20 米的矩形. 为便于管理,要在中间开辟一横两纵 共三条等宽的小道,使种植面积为 600 平方米, 则小道的宽为多少米? 若设小道的宽为x 米,则根据题意, 列方程 为 ( )
A .35 20 35x 20x 2x2 600
C .(35 2x)(20 x) 600
B .35 20 35x 2 20x 600
D .(35 x)(20 2x) 600
第 1 题图 第 4 题图 第 5 题图 第 6 题图
6.如图, 为了测量一条河流的宽度, 一测量员在河岸边相距 200 米的P 、 Q 两点分别测定对岸一棵树T 的位置, T 在P 的正北方向, 且T 在 Q 的北偏西70 方向, 则河宽(PT的长) 可以表示为( )
A .200tan70°米 B.
米 C . 200sin 70 米 D . 米
tan 70 sin 70
7.给出一种运算: 对于函数y xn ,规定y nxn 1 .例如: 若函数y x4 ,则有y 4x3 .已知函数y x3 ,则方程 y 27 的解是( )
A .x1 3 ,x2 3 B .x1 2 ,x2 2 C .x1 x2 0 D .x1 3 ,x2 = 3
(
B
.
2
D
.
4
) (
5
) (
4
) (
k
)8.下列说法正确的是( )
A.两条对角线互相垂直且相等的四边形是正方形
B.任意两个等腰三角形相似
C.一元二次方程x2 ax 2 0 ,无论a取何值, 一定有两个不相等的实数根
D.关于反比例函数y ,y 的值随x 值的增大而减小 x
9.二次函数y ax2 4x 2 的图象和一次函数y ax a(a 0) 的图象在同一平面直角坐标系中可能是( )
A. B. C . D.
10 .如图, △ABC 中,∠BAC=120°,∠ACB=45°, 分别以AB、AC 为边向三角形ABC 外部作正方形ABDE 和
正方形ACFG,连接 CE、BG 交点为 K,CE、AG 交点为 N,延长 CA 交 BG 于点 M,连接 CG.则下列结论:
①△ABG≌△AEC;②BG⊥CE;③AM=AN;④2CF2=KG CE,其中正确的有(
A .1
C .3
二.填空题(每题 3 分, 共 15 分)
11.若 b 3 ,则 a b 的值等于 . a 2 b
12.若一元二次方程ax2 bx 2022 0 有一根为x = 1 ,则 a b .
(
)个.
第
10
题图
)
13.如图, 小颖身高为160cm ,在阳光下影长AB 240cm,当她走到距离墙角(点D)150cm 处时, 她的部分影子投
射到墙上, 则投射在墙上的影子DE 的长度为 cm .
14 .如图, 在平面直角坐标系中, ABC 的边 AB //x 轴,点 A 在双曲线y (x 0) 上,点 B 在双曲线 x
y (x 0) 上,边 AC 中点D 在x 轴上, ABC的面积为 8,则 k .
x
15.如图, a / /b / /c ,直线a 与直线b 之间的距离为3 ,直线c 与直线b 之间的距离为2 3 ,等边 ABC 的三个顶
点分别在直线a 、直线 b 、直线c 上, 则等边 ABC 的边长是 .
第 13 题图 第 14 题图
第 15 题图
三.解答题(共 7 小题, 共 55 分)
16 .(8 分)解下列方程:( 1)2x2+3x+1=0; (2) ( 3) = 3 .
17 .(6 分)计算: 3 3 0 4 cos 30 .
18 .(6 分)从一副普通的扑克牌中取出四张牌, 它们的牌面数字分别为 2 ,3 ,3 ,6.
(1)将这四张扑克牌背面朝上, 洗匀,从中随机抽取一张,则抽取的这张牌的牌面数字是 3 的概率为 ;
(2)将这四张扑克牌背面朝上, 洗匀. 从中随机抽取一张, 不放回, 再从剩余的三张牌中随机抽取一张. 请利用画 树状图或列表的方法,求抽取的这两张牌的牌面数字恰好相同的概率.
19 .(8 分)在 ABC 中, AB 12 ,
(1)求证: ABD∽CBA ;
(2)求 DE 的长.
AE 14 ,BD 6 ,BC 24 ,且 BAE DAC .
20.(8 分)某药店新进一批桶装消毒液, 每桶进价 35 元, 原计划以每桶 55 元的价格销售, 为更好地助力疫情防控,
现决定降价销售. 已知这种消毒液销售量y (桶 ) 与每桶降价x (元 )(0 x 20) 之间满足一次函数关系,其图象如
图所示:
(1)求 y 与x 之间的函数关系式;
(2)在这次助力疫情防控活动中,该药店仅获利 1760 元.这种消毒液每桶实际售价多少元?
(
3
) (
5
) (
1
) (
1
) (
2
) (
1
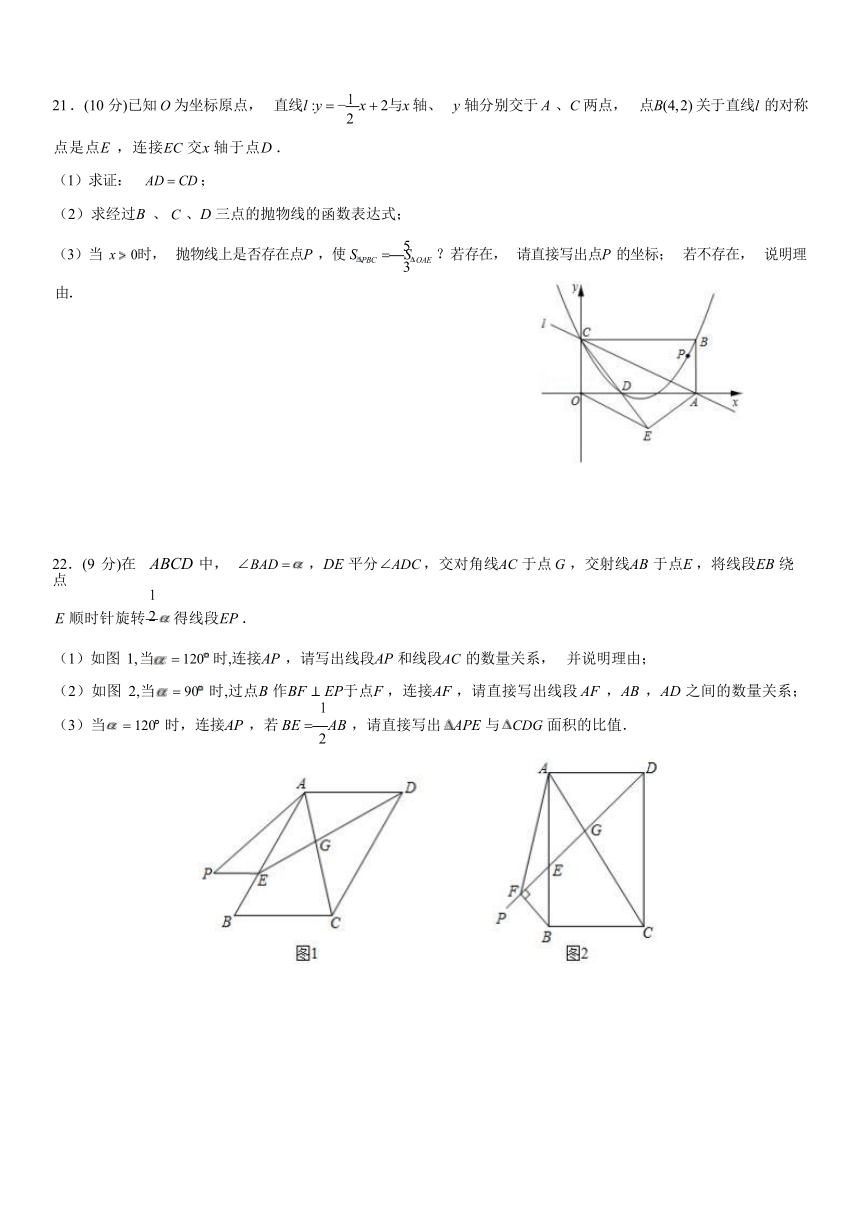
)21 .(10 分)已知 O 为坐标原点, 直线l :y x 2与x 轴、 y 轴分别交于 A 、C 两点, 点B(4, 2) 关于直线l 的对称 2
点是点E ,连接EC 交x 轴于点D .
(1)求证: AD CD ;
(2)求经过B 、 C 、D 三点的抛物线的函数表达式;
(3)当 x 0时, 抛物线上是否存在点P ,使 SPBC SOAE ?若存在, 请直接写出点P 的坐标; 若不存在, 说明理
由.
22.(9 分)在 ABCD 中, BAD ,DE 平分 ADC ,交对角线AC 于点 G ,交射线AB 于点E ,将线段EB 绕点
E 顺时针旋转 得线段EP .
(1)如图 1, 当 120 时,连接AP ,请写出线段AP 和线段AC 的数量关系, 并说明理由;
(2)如图 2,当 90 时,过点B 作BF ⊥ EP于点F ,连接AF ,请直接写出线段 AF ,AB ,AD 之间的数量关系;
(3)当 120 时,连接AP ,若 BE AB ,请直接写出 APE 与 CDG 面积的比值. 2
(
1
) (
2
1
) (
1
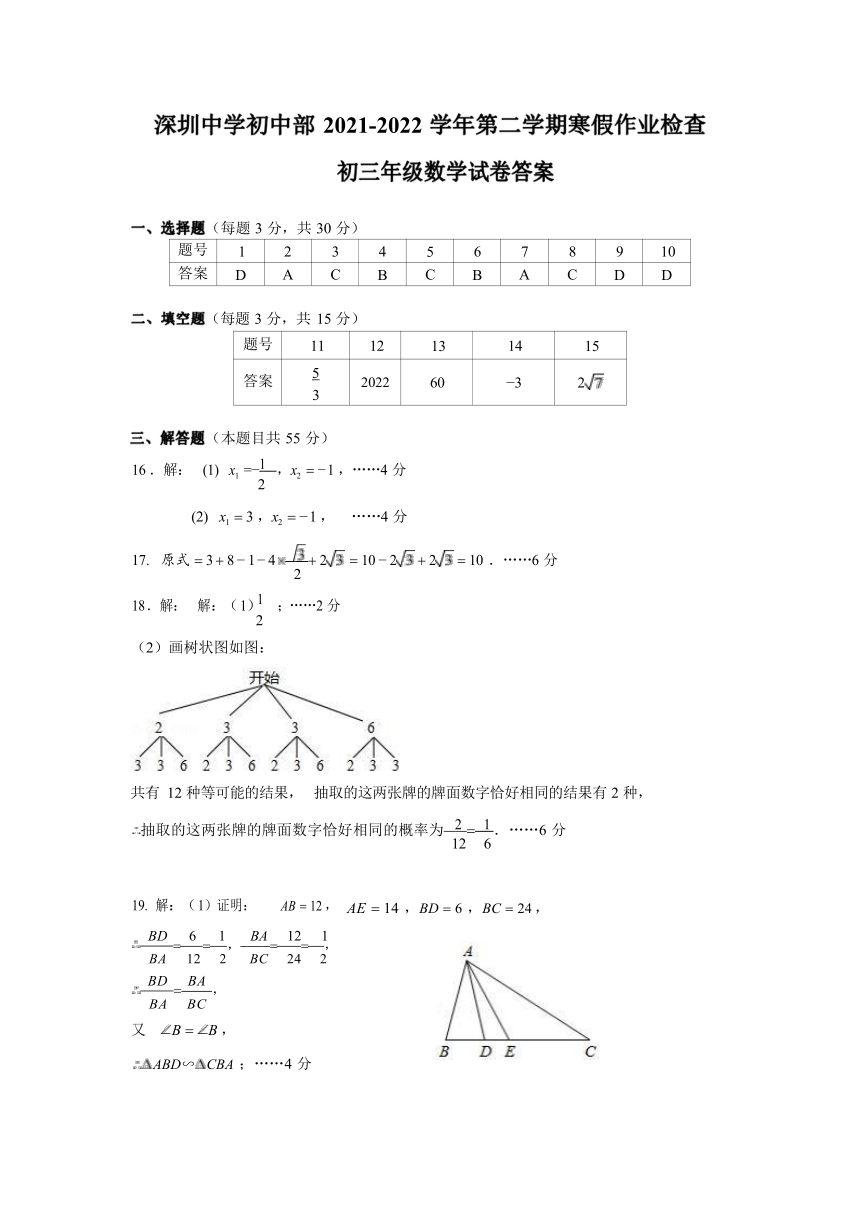
)深圳中学初中部 2021-2022 学年第二学期寒假作业检查
初三年级数学试卷答案
一、选择题(每题 3 分,共 30 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C B C B A C D D
二、填空题(每题 3 分,共 15 分)
题号 11 12 13 14 15
答案 5 3 2022 60 3 2
三、解答题(本题目共 55 分)
16 .解: (1) x1 = ,x2 1 ,……4 分 2
(2) x1 3 ,x2 1 , ……4 分
17. 原式 3 8 1 4 2 10 2 2 10 .……6 分 2
18 .解: 解:( 1) ;……2 分
2
(2)画树状图如图:
共有 12 种等可能的结果, 抽取的这两张牌的牌面数字恰好相同的结果有 2 种,
抽取的这两张牌的牌面数字恰好相同的概率为 .……6 分 12 6
19. 解:( 1)证明: AB 12 ,
BD 6 1 BA 12 1
, ,
BA 12 2 BC 24 2
BD BA
,
BA BC
又 B B ,
ABD∽CBA ;……4 分
AE 14 ,BD 6 ,BC 24 ,
(
b
100
) (
2
) (
1
)
(2) ABD∽CBA ,
BAD C ,
BAE DAC ,
BAD CAE ,
C CAE ,
CE AE 14 ,
DE BC BD CE 24 6 14
4 .……8 分
20. 解:( 1)设 y 与x 之间的函数关系式为: y kx b ,
将点(1,110) 、(3,130) 代入一次函数表达式得:
(
解得
:
,
)k 10
故函数的表达式为: y 10x 100 ;……4 分
110 k b
,
130 3k b
(2)由题意得: (10x 100) (55 x 35) 1760 ,
整理, 得x2 10x 24 0 .
解得x1 12 ,x2 2 (舍).
所以55 x 43 .
答:这种消毒液每桶实际售价 43 元. ……8 分
21 .(1)证明: y x 2 与x 轴、
A(4, 0) , C(0, 2) ,
B(4, 2) ,
OA / /BC ,
BCA OAC ,
点B(4, 2) 关于直线l 的对称点是点E
ACD ACB ,
ACD OAC ,
AD CD ;……3 分
y 轴分别交于 A 、 C 两点,
(
2
) (
3
) (
2
2
) (
3
5
4
)(2)解: 设OD m,由对称可得 CE BC 4 , AE AB OC 2 , AED B 90 , CD AD 4 m ,
在RtOCD 中, OD2 OC2 CD2 , m2 22 (4 m)2 ,
3 3
m , D( , 0) ,
设经过B 、 C 、D 三点的抛物线的函数表达式为:
把B(4, 2) , C(0, 2) ,D( ,0) 代入得:
c 2 16a 4b c 2 ,解得: (
a
b
c
0
)9 3 4 2 (
a
) (
15
32
) 8 b . 15 c 2
经过B , C ,D 三点的抛物线的函数表达式为:
y ax2 bx c ,
(
y
8
x
2
32
x
2
;
……
7
分
)15 15
(3)存在,点 P 的坐标为( ,0) 或 ( ,0) 或 ( ,4) .……10 分 2 2 2
22.(1) = ; ……1 分
方法一:如图 1,连接PB ,PC ,
四边形ABCD 是平行四边形, AD / /BC ,AB / /CD ,
120 ,即 BAD 120 ,
B ADC 60 , BEP 60 B , 由旋转知: EP EB , BPE是等边三角形, BP EP , EBP BPE 60 ,
CBP ABC EBP 120 ,
AEP 180 BEP 120 , AEP CBP ,
DE 平分 ADC , ADE CDE 30 , AED CDE 30 ADE , AD AE ,
AE BC , APE CPB(SAS) ,
AD BC ,
AP CP , APE CPB ,
APE CPE CPB CPE ,即 APC BPE 60 ,
APC是等边三角形, AP AC ;……4 分
方法二:如图 1,延长PE 交 CD 于点Q ,连接 AQ , 四边形ABCD 是平行四边形,
AD / /BC , AB / /CD ,
120 ,即 BAD 120 , B ADC 60 ,
BEP 60 B , PE / /BC / /AD ,
四边形ADQE 和四边形BCQE 是平行四边形, DE 平分 ADC , ADE CDE 30 ,
AED CDE 30 ADE , AD AE , 四边形ADQE 是菱形,
EAQ AEQ 60 , AEQ是等边三角形,
AE AQ , AQE 60 ,
四边形BCQE 是平行四边形,
PE BE CQ , B CQE 60 ,
AEP 120 , AQC AQE CQE 120 , AEP AQC , AEP AQC(SAS) , AP AC ;
(2) AB2 AD2 2AF2 ,……6 分
理由: 如图 2,连接 CF ,在 ABCD 中, BAD 90 ,
ADC ABC BAD 90 , AD BC ,
DE 平分 ADC , ADE CDE 45 , AED ADE 45 , AD AE , AE BC ,
BF ⊥ EP , BFE 90 ,
(
BEF
BAD
90
45
,
)1 1 1
2 2 2
EBF BEF 45 , BF EF ,
……4 分
FBC FBE ABC 45 90 135 , AEF 180 FEB 135 ,
CBF AEF , BCF EAF(SAS) ,
CF AF , CFB AFE ,
AFC AFE CFE CFB CFE BFE 90 ,
AC AF ,
在RtABC 中, AB2 BC2 AC2 , AB2 AD2 2AF2 ;……6 分
(
4
4
) (
2
) (
2
) (
S
CDG
2
4
) (
4
3
) (
2
) (
3
) (
3
5
) (
a
) (
a
)(3) APE 与 CDG 面积的比值为3或5 .……9 分(一个答案得 2 分, 两个答案得 3 分)
方法一:由( 1)知, BC AD AE AB BE ,
1
BE AB , AB CD , AB CD 2BE ,
2
设BE a ,则 PE AD AE a ,AB CD 2a ,
①当点E 在 AB 上时, 如图 3,过点 G 作 GM ⊥ AD于点M ,作 GN ⊥ CD 于点N , 过点 C 作CK ⊥ AD 于点K ,过点 A 作 AH ⊥ PE 的延长线于点H ,
当 120 时, B ADC 60 ,
DE 平分 ADC , GM ⊥ AD , GN ⊥ CD ,
(
S
ACD
AD
CK
a
2
a
sin
60
a
,
)1 1 2
2 2 2
1
(
S
CDG
2
CD
2
a
2
,
S
ADG
1
AD
GM
AD
a
)CD GN
2
(
S
CDG
2
S
ADG
,
S
CDG
S
ACD
a
2
,
)3 3
由( 1)知 PE / /BC , AEH B 60 ,
H 90 , AH AE sin 60 a ,
(
S
APE
PE
AH
a
a
a
,
)1 1 2
2 2 2 4
(
APE
.
)S a
a
GM GN ,
②如图 4,当点E 在AB 延长线上时,
(
由
①
同理可得:
S
CDG
S
ACD
2
a
3
a
a
,
)2 2 1 3 2
5 5 2 2 5
(
S
APE
PH
AE
a
3
a
a
,
)1 1 3 2
2 2 2 4
3 2
SAPE 4 5
SCDG 3 2 4
5
综上所述, APE 与 CDG 面积的比值为 或 .
4 4
(
) (
2
2
1
EG
1
ED
) (
(
)
,
) (
S
S
S
S
S
1
3
) (
3
5
) (
S
AEG
AE
2
3
2
9
) (
S
S
S
S
1
5
9
5
) (
3
) (
APE
APE
ADE
AEG
)方法二:如图 3 ,四边形ABCD 是平行四边形,
AD / /BC , AB / /CD ,AB CD ,
(
AEG
∽
CDG
,
AEG
(
)
2
,
,
)S AE EG AE
(
S
CD
DG
CD
)CDG
①当点E 在 AB 上时,
1
BE AB , 2
又 EG AE
DG CD
当 120 时,
1 1
AE BE AB CD ,
, ,即 3 ,
2 ED 3 EG
B ADC 60 ,
SAEG AE 2 1
(
S
CD
4
)CDG
(
AED
3
,
S
EG
)S ED
AEG
DE 平分 ADC , ADE 30 ,
AED 180 BAD ADE 30 ADE , AE AD ,
EP EB AE ,EP / /AD ,
EP AD AE , AEP DAE 120 ,
AED EAP(SAS) , SAED SEAP ,
(
APE
APE
AEG
AED
AEG
3
;
S
S
S
S
S
4
4
)CDG AEG CDG AEG CDG
②如图 4,当点E 在AB 延长线上时,
1 BE AB , 2 3 3 AE AB CD , 2 2
由①知, AD AE CD ,
2
1 1
EP BE AE AD , EP / /AD ,
3 3
(
APE
)S EP 1
(
,
S
AD
3
)ADE
EG AE 3 ED 5
, ,
DG CD 2 EG 3
(
ADE
)S ED 5
(
,
S
EG
3
)AEG
(
(
)
(
)
,
S
CD
2
4
)CDG
(
;
S
S
S
S
3
3
4
4
)CDG ADE AEG CDG
综上所述, APE 与 CDG 面积的比值为 或 .
4 4
2
) (
+
) (
200
200
) (
.
) (
D
)2021—2022 学年度第二学期寒假作业检查 初三年级数学试卷 3.5
说明:
1. 答题前,务必将自己的姓名、学号等填写在答题卷规定的位置上.
2. 考生必须在答题卷上按规定作答,凡在试卷、草稿纸上作答的,其答案一律无效.
3. 全卷共 4 页,考试时间 90 分钟, 满分 100 分.
一.单选题(每题 3 分, 共 30 分)
1.如图, 该几何体的左视图是( )
A . B . C.
2.在一个不透明的袋子里装有红球、黄球共 20 个, 这些球除颜色外都相同. 小明通过多次试验发现, 摸出红球的 频率稳定在 0.25 左右, 则袋子中红球的个数最有可能是( )
A .5 B .10 C .12 D .15
3.将抛物线y x2 2x 3向左平移 2 个单位, 再向上平移 1 个单位, 得到的抛物线的解析式为( )
A. y (x 3)2 4 B. y (x 1)2 4 C .y (x 1)2 3 D. y (x 1)2 2
4.如图, 在菱形ABCD 中, A 60 ,AB 2 ,点 M 为边AD 的中点, 连接BD 交 CM 于点N ,则 BN 的长是( )
4
A . 1 B . 3
C . D . 3
5.如图, 学校课外生物小组的试验园地的形状是长 35 米、宽 20 米的矩形. 为便于管理,要在中间开辟一横两纵 共三条等宽的小道,使种植面积为 600 平方米, 则小道的宽为多少米? 若设小道的宽为x 米,则根据题意, 列方程 为 ( )
A .35 20 35x 20x 2x2 600
C .(35 2x)(20 x) 600
B .35 20 35x 2 20x 600
D .(35 x)(20 2x) 600
第 1 题图 第 4 题图 第 5 题图 第 6 题图
6.如图, 为了测量一条河流的宽度, 一测量员在河岸边相距 200 米的P 、 Q 两点分别测定对岸一棵树T 的位置, T 在P 的正北方向, 且T 在 Q 的北偏西70 方向, 则河宽(PT的长) 可以表示为( )
A .200tan70°米 B.
米 C . 200sin 70 米 D . 米
tan 70 sin 70
7.给出一种运算: 对于函数y xn ,规定y nxn 1 .例如: 若函数y x4 ,则有y 4x3 .已知函数y x3 ,则方程 y 27 的解是( )
A .x1 3 ,x2 3 B .x1 2 ,x2 2 C .x1 x2 0 D .x1 3 ,x2 = 3
(
B
.
2
D
.
4
) (
5
) (
4
) (
k
)8.下列说法正确的是( )
A.两条对角线互相垂直且相等的四边形是正方形
B.任意两个等腰三角形相似
C.一元二次方程x2 ax 2 0 ,无论a取何值, 一定有两个不相等的实数根
D.关于反比例函数y ,y 的值随x 值的增大而减小 x
9.二次函数y ax2 4x 2 的图象和一次函数y ax a(a 0) 的图象在同一平面直角坐标系中可能是( )
A. B. C . D.
10 .如图, △ABC 中,∠BAC=120°,∠ACB=45°, 分别以AB、AC 为边向三角形ABC 外部作正方形ABDE 和
正方形ACFG,连接 CE、BG 交点为 K,CE、AG 交点为 N,延长 CA 交 BG 于点 M,连接 CG.则下列结论:
①△ABG≌△AEC;②BG⊥CE;③AM=AN;④2CF2=KG CE,其中正确的有(
A .1
C .3
二.填空题(每题 3 分, 共 15 分)
11.若 b 3 ,则 a b 的值等于 . a 2 b
12.若一元二次方程ax2 bx 2022 0 有一根为x = 1 ,则 a b .
(
)个.
第
10
题图
)
13.如图, 小颖身高为160cm ,在阳光下影长AB 240cm,当她走到距离墙角(点D)150cm 处时, 她的部分影子投
射到墙上, 则投射在墙上的影子DE 的长度为 cm .
14 .如图, 在平面直角坐标系中, ABC 的边 AB //x 轴,点 A 在双曲线y (x 0) 上,点 B 在双曲线 x
y (x 0) 上,边 AC 中点D 在x 轴上, ABC的面积为 8,则 k .
x
15.如图, a / /b / /c ,直线a 与直线b 之间的距离为3 ,直线c 与直线b 之间的距离为2 3 ,等边 ABC 的三个顶
点分别在直线a 、直线 b 、直线c 上, 则等边 ABC 的边长是 .
第 13 题图 第 14 题图
第 15 题图
三.解答题(共 7 小题, 共 55 分)
16 .(8 分)解下列方程:( 1)2x2+3x+1=0; (2) ( 3) = 3 .
17 .(6 分)计算: 3 3 0 4 cos 30 .
18 .(6 分)从一副普通的扑克牌中取出四张牌, 它们的牌面数字分别为 2 ,3 ,3 ,6.
(1)将这四张扑克牌背面朝上, 洗匀,从中随机抽取一张,则抽取的这张牌的牌面数字是 3 的概率为 ;
(2)将这四张扑克牌背面朝上, 洗匀. 从中随机抽取一张, 不放回, 再从剩余的三张牌中随机抽取一张. 请利用画 树状图或列表的方法,求抽取的这两张牌的牌面数字恰好相同的概率.
19 .(8 分)在 ABC 中, AB 12 ,
(1)求证: ABD∽CBA ;
(2)求 DE 的长.
AE 14 ,BD 6 ,BC 24 ,且 BAE DAC .
20.(8 分)某药店新进一批桶装消毒液, 每桶进价 35 元, 原计划以每桶 55 元的价格销售, 为更好地助力疫情防控,
现决定降价销售. 已知这种消毒液销售量y (桶 ) 与每桶降价x (元 )(0 x 20) 之间满足一次函数关系,其图象如
图所示:
(1)求 y 与x 之间的函数关系式;
(2)在这次助力疫情防控活动中,该药店仅获利 1760 元.这种消毒液每桶实际售价多少元?
(
3
) (
5
) (
1
) (
1
) (
2
) (
1
)21 .(10 分)已知 O 为坐标原点, 直线l :y x 2与x 轴、 y 轴分别交于 A 、C 两点, 点B(4, 2) 关于直线l 的对称 2
点是点E ,连接EC 交x 轴于点D .
(1)求证: AD CD ;
(2)求经过B 、 C 、D 三点的抛物线的函数表达式;
(3)当 x 0时, 抛物线上是否存在点P ,使 SPBC SOAE ?若存在, 请直接写出点P 的坐标; 若不存在, 说明理
由.
22.(9 分)在 ABCD 中, BAD ,DE 平分 ADC ,交对角线AC 于点 G ,交射线AB 于点E ,将线段EB 绕点
E 顺时针旋转 得线段EP .
(1)如图 1, 当 120 时,连接AP ,请写出线段AP 和线段AC 的数量关系, 并说明理由;
(2)如图 2,当 90 时,过点B 作BF ⊥ EP于点F ,连接AF ,请直接写出线段 AF ,AB ,AD 之间的数量关系;
(3)当 120 时,连接AP ,若 BE AB ,请直接写出 APE 与 CDG 面积的比值. 2
(
1
) (
2
1
) (
1
)深圳中学初中部 2021-2022 学年第二学期寒假作业检查
初三年级数学试卷答案
一、选择题(每题 3 分,共 30 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C B C B A C D D
二、填空题(每题 3 分,共 15 分)
题号 11 12 13 14 15
答案 5 3 2022 60 3 2
三、解答题(本题目共 55 分)
16 .解: (1) x1 = ,x2 1 ,……4 分 2
(2) x1 3 ,x2 1 , ……4 分
17. 原式 3 8 1 4 2 10 2 2 10 .……6 分 2
18 .解: 解:( 1) ;……2 分
2
(2)画树状图如图:
共有 12 种等可能的结果, 抽取的这两张牌的牌面数字恰好相同的结果有 2 种,
抽取的这两张牌的牌面数字恰好相同的概率为 .……6 分 12 6
19. 解:( 1)证明: AB 12 ,
BD 6 1 BA 12 1
, ,
BA 12 2 BC 24 2
BD BA
,
BA BC
又 B B ,
ABD∽CBA ;……4 分
AE 14 ,BD 6 ,BC 24 ,
(
b
100
) (
2
) (
1
)
(2) ABD∽CBA ,
BAD C ,
BAE DAC ,
BAD CAE ,
C CAE ,
CE AE 14 ,
DE BC BD CE 24 6 14
4 .……8 分
20. 解:( 1)设 y 与x 之间的函数关系式为: y kx b ,
将点(1,110) 、(3,130) 代入一次函数表达式得:
(
解得
:
,
)k 10
故函数的表达式为: y 10x 100 ;……4 分
110 k b
,
130 3k b
(2)由题意得: (10x 100) (55 x 35) 1760 ,
整理, 得x2 10x 24 0 .
解得x1 12 ,x2 2 (舍).
所以55 x 43 .
答:这种消毒液每桶实际售价 43 元. ……8 分
21 .(1)证明: y x 2 与x 轴、
A(4, 0) , C(0, 2) ,
B(4, 2) ,
OA / /BC ,
BCA OAC ,
点B(4, 2) 关于直线l 的对称点是点E
ACD ACB ,
ACD OAC ,
AD CD ;……3 分
y 轴分别交于 A 、 C 两点,
(
2
) (
3
) (
2
2
) (
3
5
4
)(2)解: 设OD m,由对称可得 CE BC 4 , AE AB OC 2 , AED B 90 , CD AD 4 m ,
在RtOCD 中, OD2 OC2 CD2 , m2 22 (4 m)2 ,
3 3
m , D( , 0) ,
设经过B 、 C 、D 三点的抛物线的函数表达式为:
把B(4, 2) , C(0, 2) ,D( ,0) 代入得:
c 2 16a 4b c 2 ,解得: (
a
b
c
0
)9 3 4 2 (
a
) (
15
32
) 8 b . 15 c 2
经过B , C ,D 三点的抛物线的函数表达式为:
y ax2 bx c ,
(
y
8
x
2
32
x
2
;
……
7
分
)15 15
(3)存在,点 P 的坐标为( ,0) 或 ( ,0) 或 ( ,4) .……10 分 2 2 2
22.(1) = ; ……1 分
方法一:如图 1,连接PB ,PC ,
四边形ABCD 是平行四边形, AD / /BC ,AB / /CD ,
120 ,即 BAD 120 ,
B ADC 60 , BEP 60 B , 由旋转知: EP EB , BPE是等边三角形, BP EP , EBP BPE 60 ,
CBP ABC EBP 120 ,
AEP 180 BEP 120 , AEP CBP ,
DE 平分 ADC , ADE CDE 30 , AED CDE 30 ADE , AD AE ,
AE BC , APE CPB(SAS) ,
AD BC ,
AP CP , APE CPB ,
APE CPE CPB CPE ,即 APC BPE 60 ,
APC是等边三角形, AP AC ;……4 分
方法二:如图 1,延长PE 交 CD 于点Q ,连接 AQ , 四边形ABCD 是平行四边形,
AD / /BC , AB / /CD ,
120 ,即 BAD 120 , B ADC 60 ,
BEP 60 B , PE / /BC / /AD ,
四边形ADQE 和四边形BCQE 是平行四边形, DE 平分 ADC , ADE CDE 30 ,
AED CDE 30 ADE , AD AE , 四边形ADQE 是菱形,
EAQ AEQ 60 , AEQ是等边三角形,
AE AQ , AQE 60 ,
四边形BCQE 是平行四边形,
PE BE CQ , B CQE 60 ,
AEP 120 , AQC AQE CQE 120 , AEP AQC , AEP AQC(SAS) , AP AC ;
(2) AB2 AD2 2AF2 ,……6 分
理由: 如图 2,连接 CF ,在 ABCD 中, BAD 90 ,
ADC ABC BAD 90 , AD BC ,
DE 平分 ADC , ADE CDE 45 , AED ADE 45 , AD AE , AE BC ,
BF ⊥ EP , BFE 90 ,
(
BEF
BAD
90
45
,
)1 1 1
2 2 2
EBF BEF 45 , BF EF ,
……4 分
FBC FBE ABC 45 90 135 , AEF 180 FEB 135 ,
CBF AEF , BCF EAF(SAS) ,
CF AF , CFB AFE ,
AFC AFE CFE CFB CFE BFE 90 ,
AC AF ,
在RtABC 中, AB2 BC2 AC2 , AB2 AD2 2AF2 ;……6 分
(
4
4
) (
2
) (
2
) (
S
CDG
2
4
) (
4
3
) (
2
) (
3
) (
3
5
) (
a
) (
a
)(3) APE 与 CDG 面积的比值为3或5 .……9 分(一个答案得 2 分, 两个答案得 3 分)
方法一:由( 1)知, BC AD AE AB BE ,
1
BE AB , AB CD , AB CD 2BE ,
2
设BE a ,则 PE AD AE a ,AB CD 2a ,
①当点E 在 AB 上时, 如图 3,过点 G 作 GM ⊥ AD于点M ,作 GN ⊥ CD 于点N , 过点 C 作CK ⊥ AD 于点K ,过点 A 作 AH ⊥ PE 的延长线于点H ,
当 120 时, B ADC 60 ,
DE 平分 ADC , GM ⊥ AD , GN ⊥ CD ,
(
S
ACD
AD
CK
a
2
a
sin
60
a
,
)1 1 2
2 2 2
1
(
S
CDG
2
CD
2
a
2
,
S
ADG
1
AD
GM
AD
a
)CD GN
2
(
S
CDG
2
S
ADG
,
S
CDG
S
ACD
a
2
,
)3 3
由( 1)知 PE / /BC , AEH B 60 ,
H 90 , AH AE sin 60 a ,
(
S
APE
PE
AH
a
a
a
,
)1 1 2
2 2 2 4
(
APE
.
)S a
a
GM GN ,
②如图 4,当点E 在AB 延长线上时,
(
由
①
同理可得:
S
CDG
S
ACD
2
a
3
a
a
,
)2 2 1 3 2
5 5 2 2 5
(
S
APE
PH
AE
a
3
a
a
,
)1 1 3 2
2 2 2 4
3 2
SAPE 4 5
SCDG 3 2 4
5
综上所述, APE 与 CDG 面积的比值为 或 .
4 4
(
) (
2
2
1
EG
1
ED
) (
(
)
,
) (
S
S
S
S
S
1
3
) (
3
5
) (
S
AEG
AE
2
3
2
9
) (
S
S
S
S
1
5
9
5
) (
3
) (
APE
APE
ADE
AEG
)方法二:如图 3 ,四边形ABCD 是平行四边形,
AD / /BC , AB / /CD ,AB CD ,
(
AEG
∽
CDG
,
AEG
(
)
2
,
,
)S AE EG AE
(
S
CD
DG
CD
)CDG
①当点E 在 AB 上时,
1
BE AB , 2
又 EG AE
DG CD
当 120 时,
1 1
AE BE AB CD ,
, ,即 3 ,
2 ED 3 EG
B ADC 60 ,
SAEG AE 2 1
(
S
CD
4
)CDG
(
AED
3
,
S
EG
)S ED
AEG
DE 平分 ADC , ADE 30 ,
AED 180 BAD ADE 30 ADE , AE AD ,
EP EB AE ,EP / /AD ,
EP AD AE , AEP DAE 120 ,
AED EAP(SAS) , SAED SEAP ,
(
APE
APE
AEG
AED
AEG
3
;
S
S
S
S
S
4
4
)CDG AEG CDG AEG CDG
②如图 4,当点E 在AB 延长线上时,
1 BE AB , 2 3 3 AE AB CD , 2 2
由①知, AD AE CD ,
2
1 1
EP BE AE AD , EP / /AD ,
3 3
(
APE
)S EP 1
(
,
S
AD
3
)ADE
EG AE 3 ED 5
, ,
DG CD 2 EG 3
(
ADE
)S ED 5
(
,
S
EG
3
)AEG
(
(
)
(
)
,
S
CD
2
4
)CDG
(
;
S
S
S
S
3
3
4
4
)CDG ADE AEG CDG
综上所述, APE 与 CDG 面积的比值为 或 .
4 4
同课章节目录
