直线与平面的位置关系
图片预览





文档简介
(共28张PPT)
异面直线所成角的定义
a
b
设a、b为两异面直线,经过空间 一 点o作直线 ,我们把 所成的锐角(或直角)叫做异面直线 a与b所成的角(或夹角).
o
aˊ
bˊ
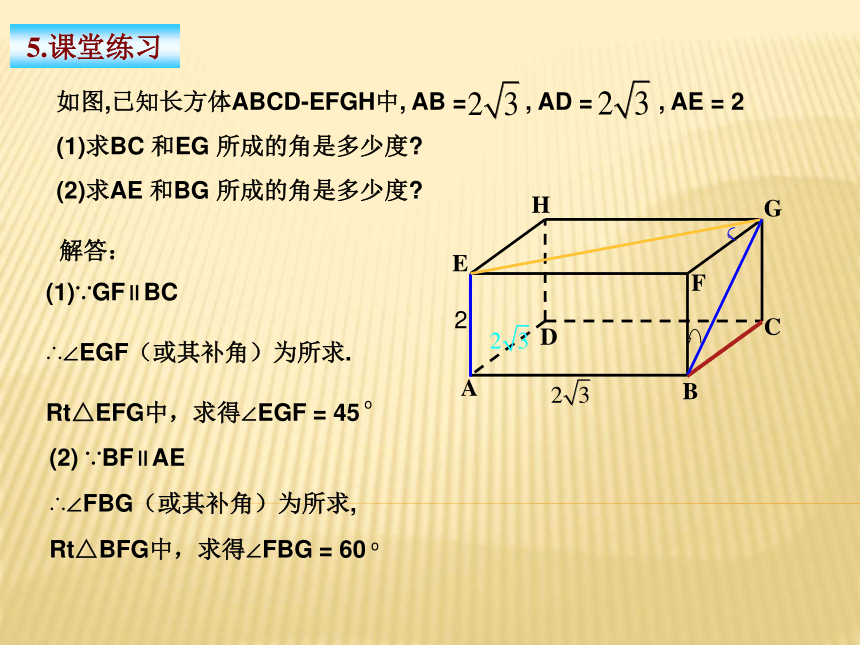
如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度
(2)求AE 和BG 所成的角是多少度
解答:
(1)∵GF∥BC
∴∠EGF(或其补角)为所求.
Rt△EFG中,求得∠EGF = 45
o
(2) ∵BF∥AE
∴∠FBG(或其补角)为所求,
Rt△BFG中,求得∠FBG = 60
o
5.课堂练习
A
B
G
F
H
E
D
C
2
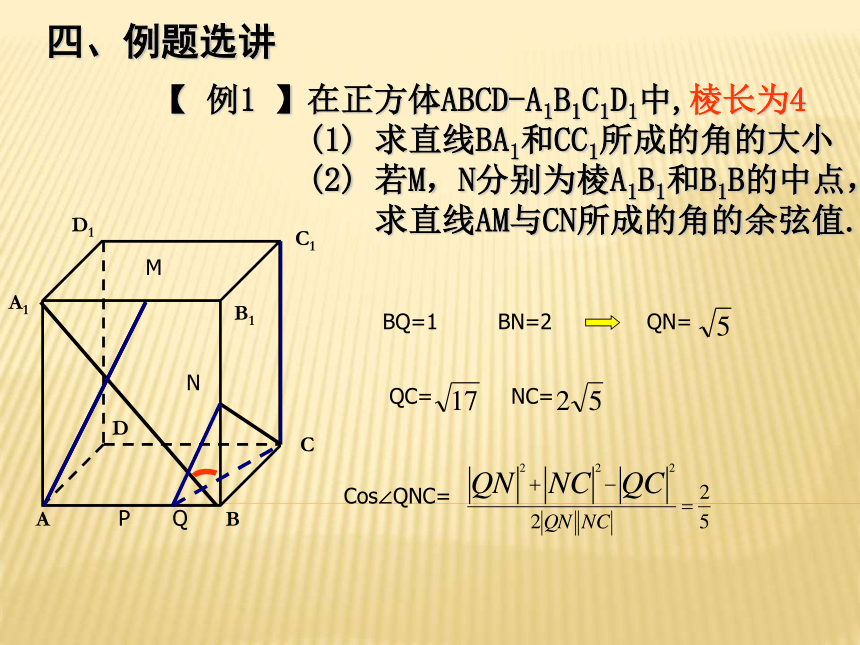
【 例1 】在正方体ABCD-A1B1C1D1中,棱长为4
(1) 求直线BA1和CC1所成的角的大小
(2) 若M,N分别为棱A1B1和B1B的中点,
求直线AM与CN所成的角的余弦值.
四、例题选讲
A1
B1
C1
D1
A
B
C
D
M
N
P
Q
BQ=1
BN=2
QN=
QC=
NC=
Cos∠QNC=
B
A
C
D
E
F
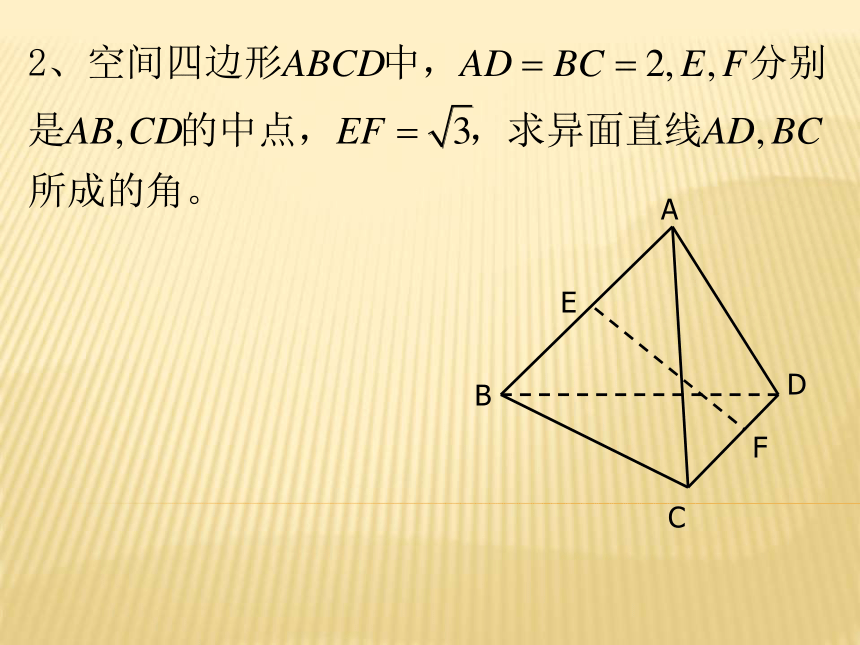
异面直线的求法:
一作(找)二证三求
(1)通过直线平移,作出异面直线所成的角,把空间
问题转化为平面问题。
(2)利用平面几何知识,求出异面直线所成角的大小。
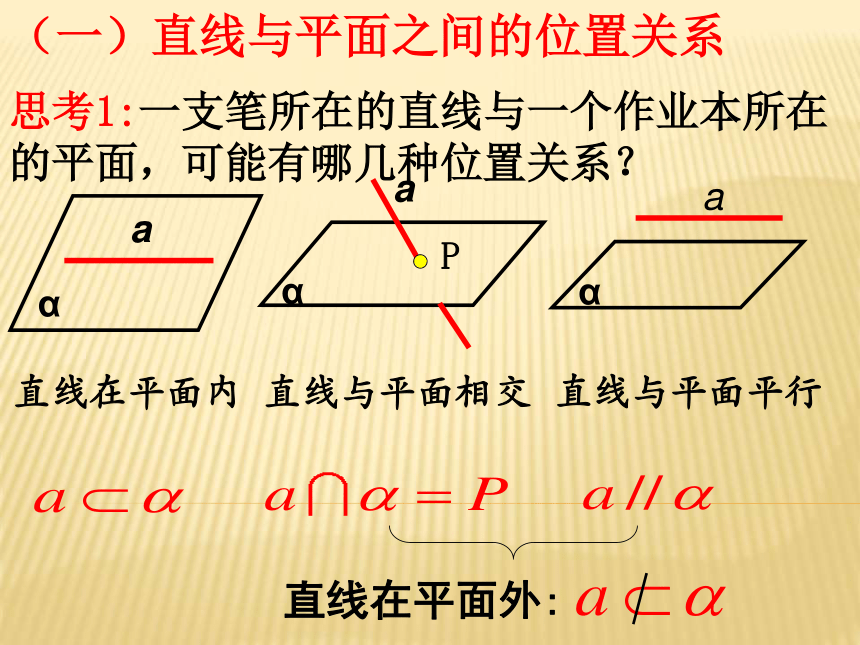
(一)直线与平面之间的位置关系
思考1:一支笔所在的直线与一个作业本所在的平面,可能有哪几种位置关系?
α
a
α
a
直线在平面外:
直线在平面内
直线与平面相交
直线与平面平行
α
a
.
P
思考2:对于一条直线和一个平面,就其公共点个数来分类有哪几种可能?
直线与平面相交---有且只有一个公共点
直线与平面平行---没有公共点.
直线在平面内---有无数个公共点
直线与平面相交与平行的情况统称为
直线在平面外.
(一)直线与平面之间的位置关系
思考3:如图,线段A′B所在直线与长方体ABCD-A′B′C′D′的六个面所在的平面有几种位置关系?
B
A
D
C
A'
B'
D'
C'
(一)直线与平面之间的位置关系
思考4:过平面外一点可作多少条直线与这个平面平行?若直线l平行于平面α,则直线l与平面α内的直线的位置关系如何?
(一)直线与平面之间的位置关系
思考5:若两条平行直线中有一条平行于一个平面,那么另一条也平行于这个平面吗?
(一)直线与平面之间的位置关系
1.下列命题中正确的个数是( )
①若直线 上有无数个点不在平面 内,则 //
②若直线 与平面 平行,则 与平面 内的任意
一条直线都平行。
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行。
④若直线 与平面 平行,
则 与平面 内的任意一条
直线都没有公共点。
练习:
若直线 不平行于平面 ,且 ,则下列结论成立的是( )
(A) 内的所有直线与 异面
(B) 内不存在与 平行的直线
(C) 内存在唯一的直线与 平行
(D) 内的直线与 都相交
A
α
a
B
2.
3.平行于同一平面的两条直线是否平行?
4.过平面外一点与这平面平行的直线有多
少条?
不一定
无数条
(二)平面与平面之间的位置关系
思考1:拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种变化?
思考2:如图,围成长方体ABCD-A1B1C1D1的六个面,两两之间的位置关系有几种?
B
A
C
D
A1
B1
C1
D1
思考3:由上面的观察和分析可知,两个平面的位置关系只有两种,即两个平面平行,两个平面相交.这两种位置关系的基本特征是什么?
(1)两个平面平行---没有公共点;
(2)两个平面相交---有一条公共直线.
(二)平面与平面之间的位置关系
思考4:下图表示两平面之间的两种位置,如何用符号语言描述这两种位置关系?
α
β
(二)平面与平面之间的位置关系
思考5:已知平面α,β和直线a,b,且α∥β, ,则直线a与平面 β的位置关系如何?直线a与直线b的位置关系如何?
α
β
a
b
(二)平面与平面之间的位置关系
例1 给出下列四个命题:
(1)若直线l上有无数个点不在平面α内,则l∥α.
(2)若直线l与平面α平行,则l与平面α内的任意一条直线都平行.
(3)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.
(4)若直线l在平面α内,且l与平面β平行,则平面α与平面β平行.
其中正确命题的个数共有 _个.
典例剖析
1
例2 如图,正方体ABCD-A′B′C′D′的棱长为8,M,N,P分别是A′B′,AD,
B B′的中点.
(1)画出过点M,N,P的平面与平面
ABCD的交线以及与平面BB′C′C的交线;
(2)设平面PMN与棱BC交于点Q,求PQ的长.
A′
B′
C′
D′
A
B
C
D
M
N
P
典例剖析
A′
B′
C′
D′
A
B
C
D
M
N
P
N
E
Q
F
直线与平面的位置关系
平面与平面的位置关系
练习
D
C
下列语句正确的个数为
⑸⑹⑺⑻
练习
A
练习
4.
C
小结
作业
1.阅读教材第48页至第50页
2.教材第51页A组第4,5,6题
异面直线所成角的定义
a
b
设a、b为两异面直线,经过空间 一 点o作直线 ,我们把 所成的锐角(或直角)叫做异面直线 a与b所成的角(或夹角).
o
aˊ
bˊ
如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度
(2)求AE 和BG 所成的角是多少度
解答:
(1)∵GF∥BC
∴∠EGF(或其补角)为所求.
Rt△EFG中,求得∠EGF = 45
o
(2) ∵BF∥AE
∴∠FBG(或其补角)为所求,
Rt△BFG中,求得∠FBG = 60
o
5.课堂练习
A
B
G
F
H
E
D
C
2
【 例1 】在正方体ABCD-A1B1C1D1中,棱长为4
(1) 求直线BA1和CC1所成的角的大小
(2) 若M,N分别为棱A1B1和B1B的中点,
求直线AM与CN所成的角的余弦值.
四、例题选讲
A1
B1
C1
D1
A
B
C
D
M
N
P
Q
BQ=1
BN=2
QN=
QC=
NC=
Cos∠QNC=
B
A
C
D
E
F
异面直线的求法:
一作(找)二证三求
(1)通过直线平移,作出异面直线所成的角,把空间
问题转化为平面问题。
(2)利用平面几何知识,求出异面直线所成角的大小。
(一)直线与平面之间的位置关系
思考1:一支笔所在的直线与一个作业本所在的平面,可能有哪几种位置关系?
α
a
α
a
直线在平面外:
直线在平面内
直线与平面相交
直线与平面平行
α
a
.
P
思考2:对于一条直线和一个平面,就其公共点个数来分类有哪几种可能?
直线与平面相交---有且只有一个公共点
直线与平面平行---没有公共点.
直线在平面内---有无数个公共点
直线与平面相交与平行的情况统称为
直线在平面外.
(一)直线与平面之间的位置关系
思考3:如图,线段A′B所在直线与长方体ABCD-A′B′C′D′的六个面所在的平面有几种位置关系?
B
A
D
C
A'
B'
D'
C'
(一)直线与平面之间的位置关系
思考4:过平面外一点可作多少条直线与这个平面平行?若直线l平行于平面α,则直线l与平面α内的直线的位置关系如何?
(一)直线与平面之间的位置关系
思考5:若两条平行直线中有一条平行于一个平面,那么另一条也平行于这个平面吗?
(一)直线与平面之间的位置关系
1.下列命题中正确的个数是( )
①若直线 上有无数个点不在平面 内,则 //
②若直线 与平面 平行,则 与平面 内的任意
一条直线都平行。
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行。
④若直线 与平面 平行,
则 与平面 内的任意一条
直线都没有公共点。
练习:
若直线 不平行于平面 ,且 ,则下列结论成立的是( )
(A) 内的所有直线与 异面
(B) 内不存在与 平行的直线
(C) 内存在唯一的直线与 平行
(D) 内的直线与 都相交
A
α
a
B
2.
3.平行于同一平面的两条直线是否平行?
4.过平面外一点与这平面平行的直线有多
少条?
不一定
无数条
(二)平面与平面之间的位置关系
思考1:拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种变化?
思考2:如图,围成长方体ABCD-A1B1C1D1的六个面,两两之间的位置关系有几种?
B
A
C
D
A1
B1
C1
D1
思考3:由上面的观察和分析可知,两个平面的位置关系只有两种,即两个平面平行,两个平面相交.这两种位置关系的基本特征是什么?
(1)两个平面平行---没有公共点;
(2)两个平面相交---有一条公共直线.
(二)平面与平面之间的位置关系
思考4:下图表示两平面之间的两种位置,如何用符号语言描述这两种位置关系?
α
β
(二)平面与平面之间的位置关系
思考5:已知平面α,β和直线a,b,且α∥β, ,则直线a与平面 β的位置关系如何?直线a与直线b的位置关系如何?
α
β
a
b
(二)平面与平面之间的位置关系
例1 给出下列四个命题:
(1)若直线l上有无数个点不在平面α内,则l∥α.
(2)若直线l与平面α平行,则l与平面α内的任意一条直线都平行.
(3)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.
(4)若直线l在平面α内,且l与平面β平行,则平面α与平面β平行.
其中正确命题的个数共有 _个.
典例剖析
1
例2 如图,正方体ABCD-A′B′C′D′的棱长为8,M,N,P分别是A′B′,AD,
B B′的中点.
(1)画出过点M,N,P的平面与平面
ABCD的交线以及与平面BB′C′C的交线;
(2)设平面PMN与棱BC交于点Q,求PQ的长.
A′
B′
C′
D′
A
B
C
D
M
N
P
典例剖析
A′
B′
C′
D′
A
B
C
D
M
N
P
N
E
Q
F
直线与平面的位置关系
平面与平面的位置关系
练习
D
C
下列语句正确的个数为
⑸⑹⑺⑻
练习
A
练习
4.
C
小结
作业
1.阅读教材第48页至第50页
2.教材第51页A组第4,5,6题
