沪科版(2012)七年级数学下册 7.2.1 一元一次不等式组的解法(第2课时) 教案 (表格式)
文档属性
| 名称 | 沪科版(2012)七年级数学下册 7.2.1 一元一次不等式组的解法(第2课时) 教案 (表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 175.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 00:00:00 | ||
图片预览

文档简介
第7章 一元一次不等式与不等式组
7.3 一元一次不等式组
第2课时 一元一次不等式组的解法
课题 第2课时 一元一次不等式组的解法 授课人
教 学 目 标 知识技能 1.能熟练地解较复杂的一元一次不等式组,并能用数轴法或口诀法表示出不等式组的解集.2.能运用已学过的不等式的知识解决实际问题,并能求出符合实际的解集.
数学思考 体会数形结合思想方法对数学学习的重要作用,感受利用不等式组模型解决问题的必要性,培养良好的数学学习习惯.
问题解决 探索含有分母的一元一次不等式组的求解步骤,并进一步归纳总结出不等式组的解集的求法;引导学生归纳总结列一元一次不等式组模型的方法与步骤,并在分析问题的过程中发展学生分析问题的能力.
情感态度 经历从数学的角度提出问题、认识问题、解决问题的过程,感受用不等式组模型解决问题的实用性,体味独立思考和合作交流学习的乐趣.
教学重点 正确地解较复杂的一元一次不等式组并能用数轴表示其解集.
教学难点 1.一元一次不等式组解集的四种情况的理解与应用. 2.分析实际问题中的数量关系,寻找最优的不等式组模型.
授课类型 新授课 课时
教具 多媒体及课件
(续表)
教学活动
教学 步骤 师生活动 设计意图
回顾 1.已知不等式组你能求出它的非负整数解吗?2.某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元.若2元的奖品购买a件,请用含a的代数式表示另外两种奖品的件数. 复习前节课学习的不等式的解法,为本节继续学习服务.
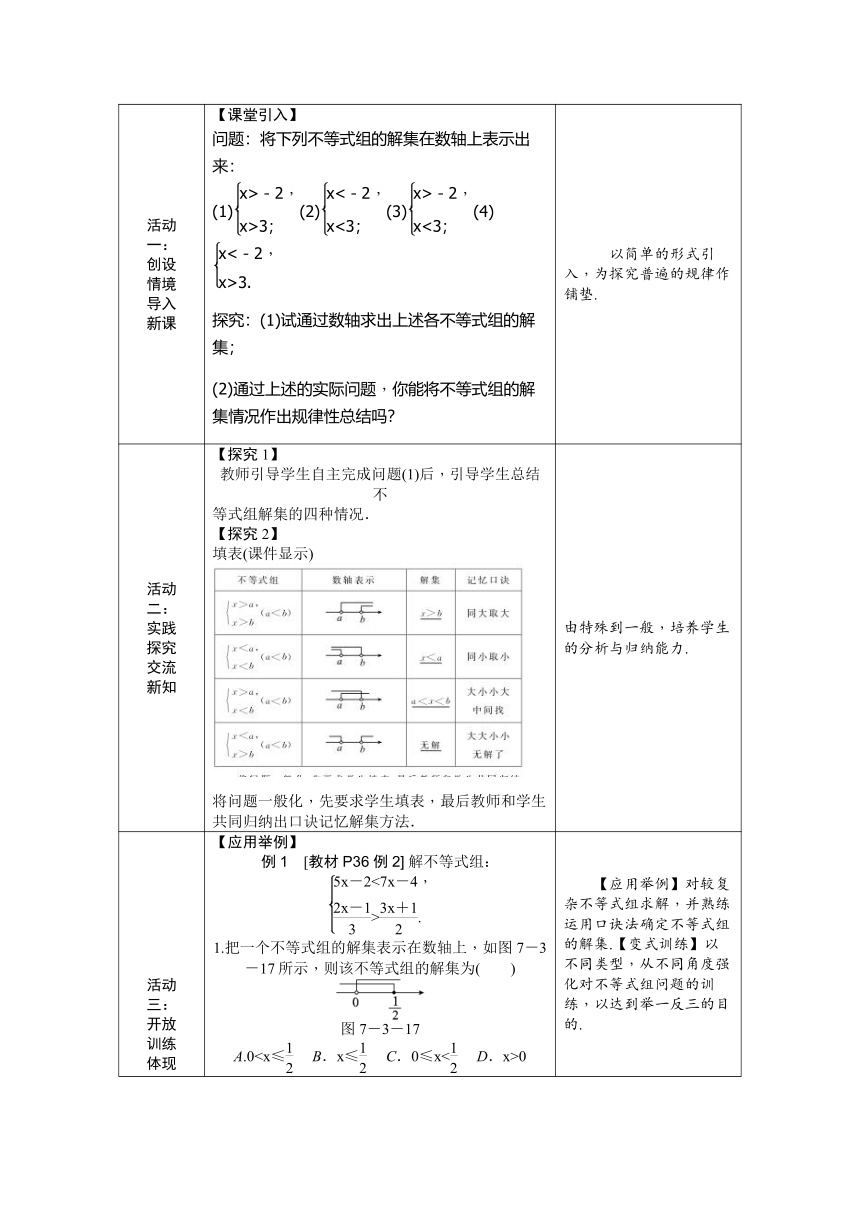
活动 一: 创设 情境 导入 新课 【课堂引入】 问题:将下列不等式组的解集在数轴上表示出来:(1)(2)(3)(4) 探究:(1)试通过数轴求出上述各不等式组的解集; (2)通过上述的实际问题,你能将不等式组的解集情况作出规律性总结吗? 以简单的形式引入,为探究普遍的规律作铺垫.
活动 二: 实践 探究 交流 新知 【探究1】 教师引导学生自主完成问题(1)后,引导学生总结不 等式组解集的四种情况. 【探究2】 填表(课件显示) 将问题一般化,先要求学生填表,最后教师和学生共同归纳出口诀记忆解集方法. 由特殊到一般,培养学生的分析与归纳能力.
活动 三: 开放 训练 体现 应用 活动 三: 开放 训练 体现 应用 【应用举例】 例1 [教材P36例2] 解不等式组: 把一个不等式组的解集表示在数轴上,如图7-3-17所示,则该不等式组的解集为( ) 图7-3-17 A.00 2.若不等式组无解,则a的取值范围是( ) A.a≥-1 B.a<-1 C.a≤1 D.a≤-1 不等式组的整数解是________. 已知方程组有正数解,则k的取值范围是________.5.解不等式组:-1<<1.6.如果关于x的方程=的解也是不等式组的一个解,求m的取值范围. 【应用举例】 例2 (选学)在我市举行的中学生安全知识竞赛中共有20道题,每一题答对得5分,答错或不答都扣 3分. (1)小李考了60分,那么小李答对了多少道题? (2)小王获得二等奖(75~85分),请你算算小王答对 了几道题? 解:(1)设小李答对了x道题. 依题意得5x-3(20-x)=60. 解得x=15.答:小李答对了15道题. (2)设小王答对了y道题,依题意得 解得≤y≤. ∵y是正整数,∴y=17或18. 答:小王答对了17道题或18道题. 【变式训练】(选练) 几位同学合影留念,已知冲一张底片需要0.80元,洗一张相片需要0.35元.在每位同学得到一张相片、共用一张底片的前提下,平均每人分摊的钱 不足0.5元,那么参加合影的同学人数( ) A.至多6人 B.至少6人 C.至多5人 D.至少5人 2.某工厂生产的一种产品,每10件的成本是35元,引进先进技术后,成本可以降低10%~15%,则改进后每件产品的成本在________元之间. 3.解放军某连队在一次执行任务中,将战士分成相同人数的8个小组,如果分配每组人数比预定人数多1名,那么战士总数将超过100人,如果每组人数比预定人数少1人,那么战士总数将不到90人,求预定每组分配的战士数. 【应用举例】对较复杂不等式组求解,并熟练运用口诀法确定不等式组的解集.【变式训练】以不同类型,从不同角度强化对不等式组问题的训练,以达到举一反三的目的.
【拓展提升】 例3 若不等式组的解集为x>a,则a的取值 范围是( ) A.a<3 B.a=3 C.a>3 D.a≥3 例4 如果不等式组的解集是30,y<0,则m的取值范围是________. 例7 (选做)某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A,B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种 造型需甲种花卉5盆,乙种花卉9盆. 某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几 种?请你帮助设计出来; (2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元? 开阔视野,培养学生的发散思维能力和建模能力.
活动 四: 课堂 总结 反思 【当堂训练】 P36练习T1,T2. 作业布置:P37习题7.3T2(3)(4),T3. 及时反馈,巩固提高.
【知识网络】 提纲挈领,重点突出.
活动 四: 课堂 总结 反思 【教学反思】 ①[授课流程反思] 情景导入的板书较长,因此要采用多媒体教学才能做到发散、增容、高效. ②[讲授效果反思] 重点要把握好不等式组的解法及解集在数轴上的表示.学生易找错公共解集. ③[师生互动反思] __________________________________________ ___________________________________________ ④[习题反思] 好题题号___________________________________ 错题题号___________________________________ 及时回顾得失,以利后继教学借鉴提高.
7.3 一元一次不等式组
第2课时 一元一次不等式组的解法
课题 第2课时 一元一次不等式组的解法 授课人
教 学 目 标 知识技能 1.能熟练地解较复杂的一元一次不等式组,并能用数轴法或口诀法表示出不等式组的解集.2.能运用已学过的不等式的知识解决实际问题,并能求出符合实际的解集.
数学思考 体会数形结合思想方法对数学学习的重要作用,感受利用不等式组模型解决问题的必要性,培养良好的数学学习习惯.
问题解决 探索含有分母的一元一次不等式组的求解步骤,并进一步归纳总结出不等式组的解集的求法;引导学生归纳总结列一元一次不等式组模型的方法与步骤,并在分析问题的过程中发展学生分析问题的能力.
情感态度 经历从数学的角度提出问题、认识问题、解决问题的过程,感受用不等式组模型解决问题的实用性,体味独立思考和合作交流学习的乐趣.
教学重点 正确地解较复杂的一元一次不等式组并能用数轴表示其解集.
教学难点 1.一元一次不等式组解集的四种情况的理解与应用. 2.分析实际问题中的数量关系,寻找最优的不等式组模型.
授课类型 新授课 课时
教具 多媒体及课件
(续表)
教学活动
教学 步骤 师生活动 设计意图
回顾 1.已知不等式组你能求出它的非负整数解吗?2.某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元.若2元的奖品购买a件,请用含a的代数式表示另外两种奖品的件数. 复习前节课学习的不等式的解法,为本节继续学习服务.
活动 一: 创设 情境 导入 新课 【课堂引入】 问题:将下列不等式组的解集在数轴上表示出来:(1)(2)(3)(4) 探究:(1)试通过数轴求出上述各不等式组的解集; (2)通过上述的实际问题,你能将不等式组的解集情况作出规律性总结吗? 以简单的形式引入,为探究普遍的规律作铺垫.
活动 二: 实践 探究 交流 新知 【探究1】 教师引导学生自主完成问题(1)后,引导学生总结不 等式组解集的四种情况. 【探究2】 填表(课件显示) 将问题一般化,先要求学生填表,最后教师和学生共同归纳出口诀记忆解集方法. 由特殊到一般,培养学生的分析与归纳能力.
活动 三: 开放 训练 体现 应用 活动 三: 开放 训练 体现 应用 【应用举例】 例1 [教材P36例2] 解不等式组: 把一个不等式组的解集表示在数轴上,如图7-3-17所示,则该不等式组的解集为( ) 图7-3-17 A.0
【拓展提升】 例3 若不等式组的解集为x>a,则a的取值 范围是( ) A.a<3 B.a=3 C.a>3 D.a≥3 例4 如果不等式组的解集是3
活动 四: 课堂 总结 反思 【当堂训练】 P36练习T1,T2. 作业布置:P37习题7.3T2(3)(4),T3. 及时反馈,巩固提高.
【知识网络】 提纲挈领,重点突出.
活动 四: 课堂 总结 反思 【教学反思】 ①[授课流程反思] 情景导入的板书较长,因此要采用多媒体教学才能做到发散、增容、高效. ②[讲授效果反思] 重点要把握好不等式组的解法及解集在数轴上的表示.学生易找错公共解集. ③[师生互动反思] __________________________________________ ___________________________________________ ④[习题反思] 好题题号___________________________________ 错题题号___________________________________ 及时回顾得失,以利后继教学借鉴提高.
