沪科版(2012)初中数学七年级下册7.3.2不等式复习教案(表格式)
文档属性
| 名称 | 沪科版(2012)初中数学七年级下册7.3.2不等式复习教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 43.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 00:00:00 | ||
图片预览

文档简介
学 科 数学 课 题 不等式复习
授课老师 课题类型 复习课
教学课时 教学方法
教学目标 知识与技能: 1.熟练掌握不等式的基本性质以及解法。2.解决不等式的含参问题
过程与方法: 学会独立思考,掌握数形结合思想。情感态度价值观:培养合情推理能力,提高合作交流意识,体会数学源于生活又服务于生活, 激发学习热情。
教学重点 重点:不等式的基本性质
教学难点 难点:用数形结合的思想解决含参问题。
教学用具 多媒体课件,直尺。
教学过程
环节 教师活动 学生活动 设计意图
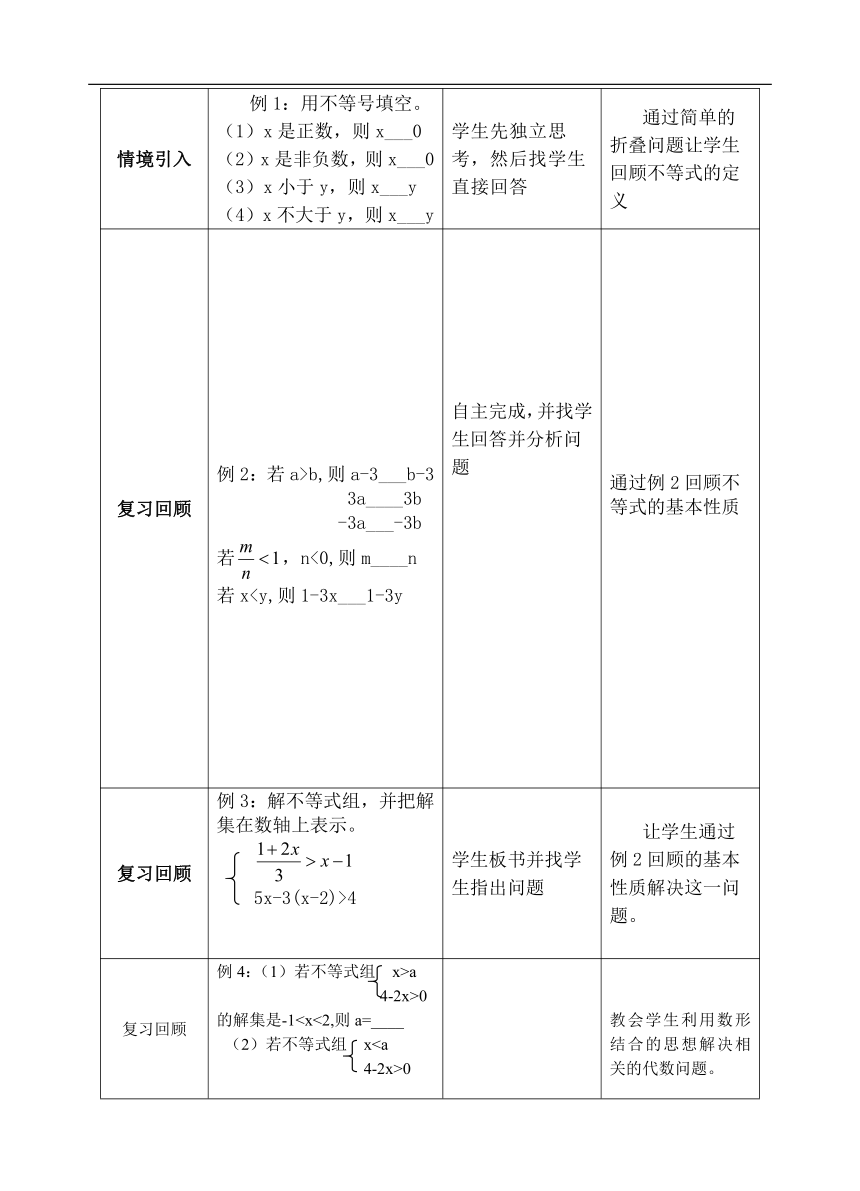
情境引入 例1:用不等号填空。(1)x是正数,则x___0(2)x是非负数,则x___0(3)x小于y,则x___y(4)x不大于y,则x___y 学生先独立思考,然后找学生直接回答 通过简单的折叠问题让学生回顾不等式的定义
复习回顾 例2:若a>b,则a-3___b-3 3a____3b -3a___-3b若,n<0,则m____n若x复习回顾 例3:解不等式组,并把解集在数轴上表示。 5x-3(x-2)>4 学生板书并找学生指出问题 让学生通过例2回顾的基本性质解决这一问题。
复习回顾 例4:(1)若不等式组 x>a 4-2x>0的解集是-10的解集是x<2,则a____(3)若不等式组 x>a 4-2x>0有解,则a___(4)若不等式组 x>a 4-2x>0有4个整数解,则a____ 书面练习,学生独立完成,教师点评。各抒己见,谈谈自己的看法。最后达成共识。 教会学生利用数形结合的思想解决相关的代数问题。
难点突破激流勇进 例:若不等式组 x+15>2x-6 2x+2课堂小结 1.本节课学习了哪些知识?2.本节课涉及了哪些思想方法?
板书设计 例1:用不等号填空。(1)x是正数,则x___0(2)x是非负数,则x___0(3)x小于y,则x___y(4)x不大于y,则x___y 不等式
例2:若a>b,则a-3___b-3 3a____3b -3a___-3b若,n<0,则m____n若xa 4-2x>0的解集是-1a 4-2x>0有解,则a___(4)若不等式组 x>a 4-2x>0有4个整数解,则a____
例3:解不等式组,并把解集在数轴上表示。 5x-3(x-2)>4
教学反思
本节课的设计思路是利用例1回顾不等式的定义,然后通过例2复习不等式的性质,有了不等式的性质解决解不等式的问题,然后在解不等式的基础上利用数形结合思想解决不等式的含参问题。但是,本节课也存在一些问题,现总结如下:本节课前面题目都较为简单,对于优等生的帮助并不太大。在例4中,关于临界点的问题,部分学生还不是太懂,说明课堂上对细节问题的解释还不够到位。
授课老师 课题类型 复习课
教学课时 教学方法
教学目标 知识与技能: 1.熟练掌握不等式的基本性质以及解法。2.解决不等式的含参问题
过程与方法: 学会独立思考,掌握数形结合思想。情感态度价值观:培养合情推理能力,提高合作交流意识,体会数学源于生活又服务于生活, 激发学习热情。
教学重点 重点:不等式的基本性质
教学难点 难点:用数形结合的思想解决含参问题。
教学用具 多媒体课件,直尺。
教学过程
环节 教师活动 学生活动 设计意图
情境引入 例1:用不等号填空。(1)x是正数,则x___0(2)x是非负数,则x___0(3)x小于y,则x___y(4)x不大于y,则x___y 学生先独立思考,然后找学生直接回答 通过简单的折叠问题让学生回顾不等式的定义
复习回顾 例2:若a>b,则a-3___b-3 3a____3b -3a___-3b若,n<0,则m____n若x
复习回顾 例4:(1)若不等式组 x>a 4-2x>0的解集是-1
难点突破激流勇进 例:若不等式组 x+15>2x-6 2x+2
板书设计 例1:用不等号填空。(1)x是正数,则x___0(2)x是非负数,则x___0(3)x小于y,则x___y(4)x不大于y,则x___y 不等式
例2:若a>b,则a-3___b-3 3a____3b -3a___-3b若,n<0,则m____n若x
例3:解不等式组,并把解集在数轴上表示。 5x-3(x-2)>4
教学反思
本节课的设计思路是利用例1回顾不等式的定义,然后通过例2复习不等式的性质,有了不等式的性质解决解不等式的问题,然后在解不等式的基础上利用数形结合思想解决不等式的含参问题。但是,本节课也存在一些问题,现总结如下:本节课前面题目都较为简单,对于优等生的帮助并不太大。在例4中,关于临界点的问题,部分学生还不是太懂,说明课堂上对细节问题的解释还不够到位。
