第一章 电场 专题讲座 课件(人教选修3-1)
文档属性
| 名称 | 第一章 电场 专题讲座 课件(人教选修3-1) |  | |
| 格式 | zip | ||
| 文件大小 | 385.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-12-28 20:29:11 | ||
图片预览








文档简介
课件28张PPT。 带电粒子在电场中的运动,是一个综合电场力、电势能的力学问题,研究的方法与质点动力学相同,它同样遵循运动的合成与分解、牛顿运动定律、动能定理等力学规律。处理问题的要点是要注意区分不同的物理过程,弄清在不同的物理过程中物体的受力情况及运动性质,并选用相应的物理规律。 为了加深对这部分知识的理解与应用,下面就处理这类问题的常见思想、方法分类加以举例。一、用动力学观点分析带电粒子的运动过程
带电粒子的运动情况取决于它的受力情况及初始状态,处理这类问题时,首先要对物体进行受力分析(包括静电力),通过受力分析可以判断带电粒子的运动性质并根据其初始状态确定其运动轨迹。
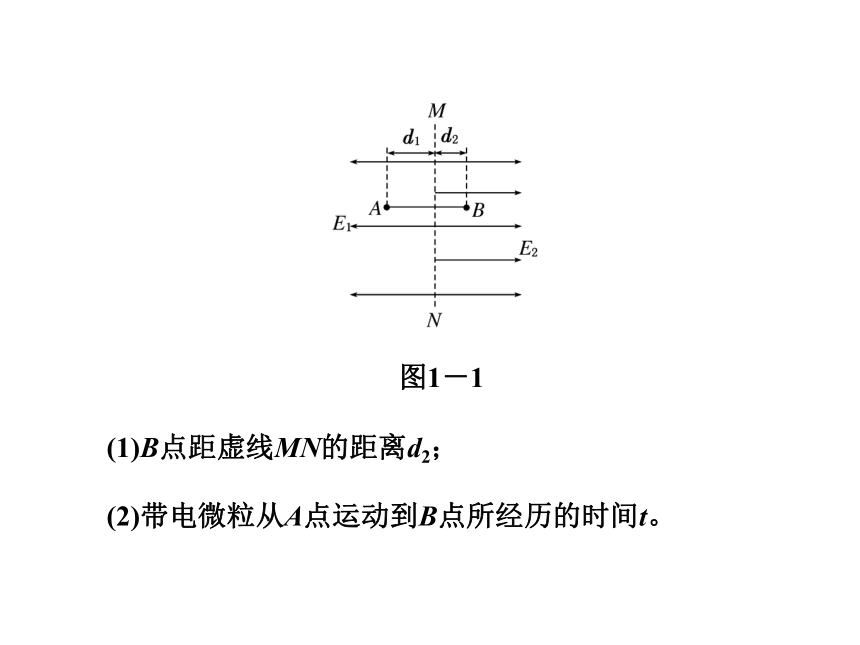
处理这类问题常与牛顿运动定律以及运动学公式等规律相结合。 [例1] (2011·福建高考)反射式速调管是常用的微波器件之一,它利用电子团在电场中的振荡来产生微波,其振荡原理与下述过程类似。如图1-1所示,在虚线MN两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在A、B两点间往返运动。已知电场强度的大小分别是E1=2.0×103 N/C和E2=4.0×103 N/C,方向如图所示。带电微粒质量m=1.0×10-20 kg,带电量q=-1.0×10-9 C,A点距虚线MN的距离d1=1.0 cm,不计带电微粒的重力,忽略相对论效应。求: 图1-1(1)B点距虚线MN的距离d2;
(2)带电微粒从A点运动到B点所经历的时间t。[答案] (1)0.50 cm (2)1.5×10-8 s 二、用运动的分解思想处理带电粒子的曲线运动
当带电粒子以某一速度射入匀强电场或复合场(电场及重力场)中时,由于粒子的受力方向与运动方向不在一条直线上而做曲线运动。处理这类问题时,常常应用运动的合成与分解法,即将带电粒子较复杂的曲线运动分解为沿电场方向和垂直于电场方向的两个运动来求解。 [例2] 一个带负电的小球质量为m,带
电量为q,在一个如图1-2所示的平行板电
容器的右侧边被竖直上抛,最后落在电容
器左侧边缘同一高度处,两板间距离为d,
板间电压为U,求小球能达到的最大高度H及抛出时的初速度v0。图1-2 三、用功能观点处理带电粒子在电场中的运动问题
由于电场力做功与带电粒子在电场中运动的路径无关,只决定于始末位置的电势差,即WAB=qUAB。对于受变力作用的带电粒子的运动,借助于能量的观点处理往往会更简捷,具体的处理方法通常有两种: (1)用动能定理处理,思维顺序一般为:①弄清研究对象,明确研究的物理过程。②分析物体在所研究的过程中的受力情况,弄清哪些力做功,做正功还是做负功。③弄清所研究的过程的初、末动能。④根据列出的方程求解。
(2)用包括静电势能和内能在内的能量守恒定律处理。列式的方法主要有两种:①从初、末状态的能量相等列方程。②从某些能量的减少量等于另一些能量的增加量列方程。 [例3] 质量为m,电荷量为q的质
点,在静电力作用下以恒定速率v沿圆
弧从A点运动到B点,其速度方向改变
角度为θ(弧度),AB弧长为s,如图1-3所示,则AB两点间的电势差UA-UB=________,AB弧中点的场强大小E=________(不计重力)。图1-3 四、用极限思想分析临界问题
涉及带电粒子在电场中运动的临界问题时,关键是找到临界状态所对应的临界条件,而临界条件可以借助极限法进行分析。 [例4] 一束电子流在经U=5 000
V的加速电压加速后,在距两极板等
距处垂直进入平行板间的匀强电场,
如图1-4所示,若两板间距d=
1.0 cm,板长l=5.0 cm,那么,要使电子能从平行板间飞出,两个极板上最大能加多大的电压。图1-4[答案] 400 V 五、运用等效思想建立复合场模型处理相关问题
匀强电场有许多性质与重力场非常相似,所以在解有关电场问题的过程中,可以将电场与重力场加以类比,在力、能量、做功方面寻找它们的共性,将匀强电场等效为重力场,按照重力场中物体的运动规律解决电场问题。 [例5] 如图1-5所示,在水平向
右的匀强电场中,有一质量为m、带
正电的小球 ,用长为l的绝缘细线悬
挂于O点,当小球静止时细线与竖直
方向的夹角为θ。
现给小球一个初速度,使小球恰能在竖直平面内做圆周运动,试问:图1-5(1)小球在做圆周运动的过程中,在哪一位置速度最小?速度最小值为多少?
(2)小球的初速度应为多大?
带电粒子的运动情况取决于它的受力情况及初始状态,处理这类问题时,首先要对物体进行受力分析(包括静电力),通过受力分析可以判断带电粒子的运动性质并根据其初始状态确定其运动轨迹。
处理这类问题常与牛顿运动定律以及运动学公式等规律相结合。 [例1] (2011·福建高考)反射式速调管是常用的微波器件之一,它利用电子团在电场中的振荡来产生微波,其振荡原理与下述过程类似。如图1-1所示,在虚线MN两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在A、B两点间往返运动。已知电场强度的大小分别是E1=2.0×103 N/C和E2=4.0×103 N/C,方向如图所示。带电微粒质量m=1.0×10-20 kg,带电量q=-1.0×10-9 C,A点距虚线MN的距离d1=1.0 cm,不计带电微粒的重力,忽略相对论效应。求: 图1-1(1)B点距虚线MN的距离d2;
(2)带电微粒从A点运动到B点所经历的时间t。[答案] (1)0.50 cm (2)1.5×10-8 s 二、用运动的分解思想处理带电粒子的曲线运动
当带电粒子以某一速度射入匀强电场或复合场(电场及重力场)中时,由于粒子的受力方向与运动方向不在一条直线上而做曲线运动。处理这类问题时,常常应用运动的合成与分解法,即将带电粒子较复杂的曲线运动分解为沿电场方向和垂直于电场方向的两个运动来求解。 [例2] 一个带负电的小球质量为m,带
电量为q,在一个如图1-2所示的平行板电
容器的右侧边被竖直上抛,最后落在电容
器左侧边缘同一高度处,两板间距离为d,
板间电压为U,求小球能达到的最大高度H及抛出时的初速度v0。图1-2 三、用功能观点处理带电粒子在电场中的运动问题
由于电场力做功与带电粒子在电场中运动的路径无关,只决定于始末位置的电势差,即WAB=qUAB。对于受变力作用的带电粒子的运动,借助于能量的观点处理往往会更简捷,具体的处理方法通常有两种: (1)用动能定理处理,思维顺序一般为:①弄清研究对象,明确研究的物理过程。②分析物体在所研究的过程中的受力情况,弄清哪些力做功,做正功还是做负功。③弄清所研究的过程的初、末动能。④根据列出的方程求解。
(2)用包括静电势能和内能在内的能量守恒定律处理。列式的方法主要有两种:①从初、末状态的能量相等列方程。②从某些能量的减少量等于另一些能量的增加量列方程。 [例3] 质量为m,电荷量为q的质
点,在静电力作用下以恒定速率v沿圆
弧从A点运动到B点,其速度方向改变
角度为θ(弧度),AB弧长为s,如图1-3所示,则AB两点间的电势差UA-UB=________,AB弧中点的场强大小E=________(不计重力)。图1-3 四、用极限思想分析临界问题
涉及带电粒子在电场中运动的临界问题时,关键是找到临界状态所对应的临界条件,而临界条件可以借助极限法进行分析。 [例4] 一束电子流在经U=5 000
V的加速电压加速后,在距两极板等
距处垂直进入平行板间的匀强电场,
如图1-4所示,若两板间距d=
1.0 cm,板长l=5.0 cm,那么,要使电子能从平行板间飞出,两个极板上最大能加多大的电压。图1-4[答案] 400 V 五、运用等效思想建立复合场模型处理相关问题
匀强电场有许多性质与重力场非常相似,所以在解有关电场问题的过程中,可以将电场与重力场加以类比,在力、能量、做功方面寻找它们的共性,将匀强电场等效为重力场,按照重力场中物体的运动规律解决电场问题。 [例5] 如图1-5所示,在水平向
右的匀强电场中,有一质量为m、带
正电的小球 ,用长为l的绝缘细线悬
挂于O点,当小球静止时细线与竖直
方向的夹角为θ。
现给小球一个初速度,使小球恰能在竖直平面内做圆周运动,试问:图1-5(1)小球在做圆周运动的过程中,在哪一位置速度最小?速度最小值为多少?
(2)小球的初速度应为多大?
