人教版2021--2022八年级(下)数学第十六单元质量检测试卷B(含解析)
文档属性
| 名称 | 人教版2021--2022八年级(下)数学第十六单元质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 990.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 20:22:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2021-2022学年八年级(下)第十六章二次根式检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 下列二次根式中,最简二次根式为
A. B. C. D.
2. 若 化简后的值可以和 合并,则 的值可以是
A. B. C. D.
3. 下列计算错误的是
A. B. C. D.
4. 若 ,则
A. B. C. D.
5. 与 结果相同的是
A. B. C. D.
6. 如图,矩形内有两个相邻的正方形,其面积分别为 和 ,则图中阴影部分的面积为
A. B. C. D.
7. 要使 有意义,则 的取值范围为
A. B. C. D.
8. ,, 三个数的大小关系是
A. B. C. D.
9. 二次根式 的一个有理化因式是
A. B. C. D.
10. 我们可以用平方之后再开方的方式来化简一些有特点的无理数,如:对于 ,设 ,易知 ,故 ,由 ,解得 ,即 .根据以上方法,化简 后的结果为
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 化简: .
12. 若 ,则 .
13. 代数式 在实数范围内有意义,则 的取值范围是 .
14. .
15. 若最简二次根式 与 的被开方数相同,则 .
16. 化简: 的结果是 .
三、解答题(共9小题;共72分)
17. (8分)化简:
(1);
(2);
(3);
(4).
18. (8分)计算:.
19. (8分)实数 在什么范围内取值时,下列各式表示二次根式
.
20. (8分)阅读下面的材料,解答后面提出的问题:
黑白双雄,纵横江湖;双剑合璧,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如:,,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式的除法可以这样解:,.像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.
解决问题:
(1) 的一个有理化因式是 ,将 分母有理化得 .
(2)已知 ,,则 .
(3)利用上面所提供的解法,请化简 .
21.(8分) 现有一个用铁网围成的长、宽之比为 的猪舍,需将面积扩大 ,方案有两种.方案一:再另外单独围一个正方形猪舍;方案二:将原猪舍改成正方形猪舍.你认为哪个方案比较好 为什么
22.(8分) 观察下列一组等式,再解答问题:
,,,,.
(1)利用上面的规律,计算下列式子的值.
.
(2)利用上面的规律,试比较 与 的大小.
23. (8分)计算
(1);
(2)
24. (8分)如图,大正方形边长为 ,去掉一个边长为 的小正方形后,求留下的阴影部分的面积.(保留三个有效数字)
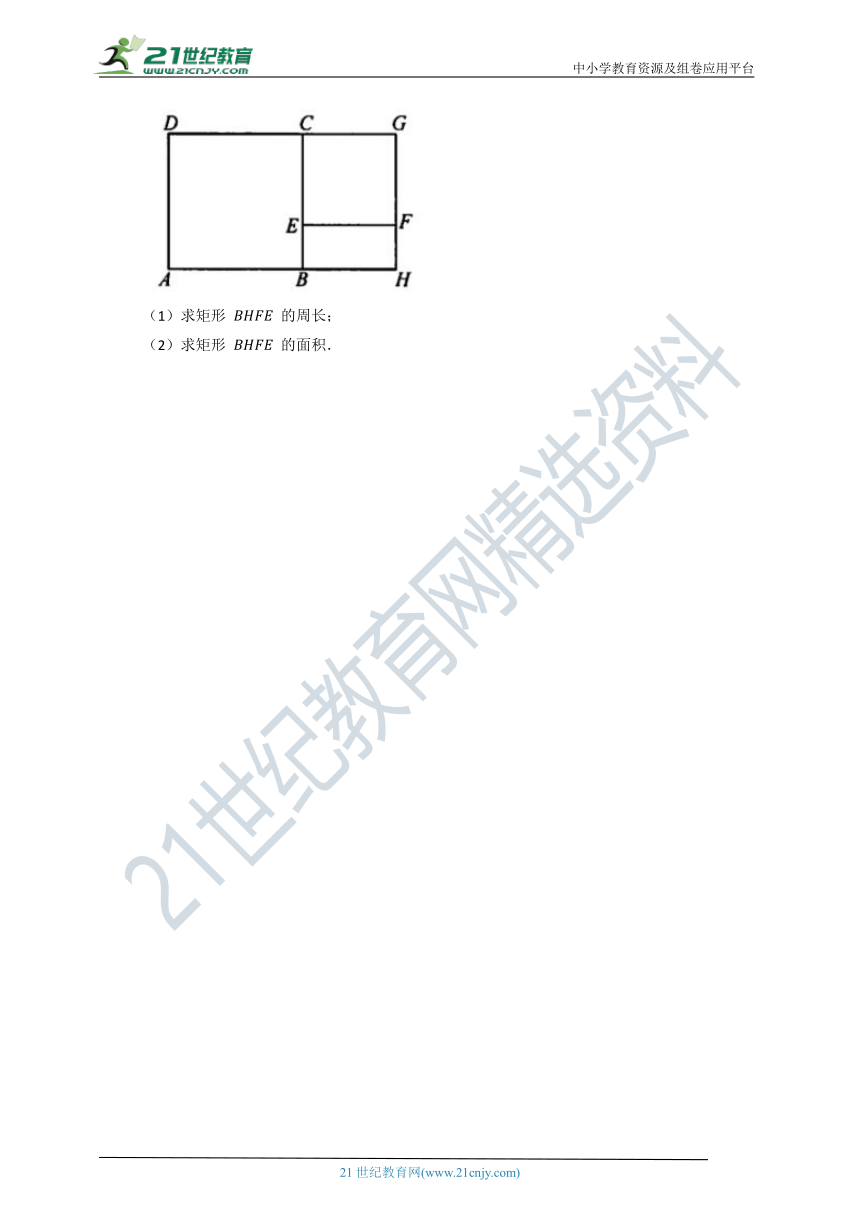
25.(8分) 如图,已知正方形 的面积为 ,正方形 的面积为 .
(1)求矩形 的周长;
(2)求矩形 的面积.
答案
第一部分
1. B
2. C
3. C 【解析】被开方数是带分数的要先化成假分数,再化简,即 .故选项C中的计算错误.
4. C
5. A
6. B 【解析】由题意可得,大正方形的边长为 ,小正方形的边长为 ,
阴影部分的面积为 ,
故选B.
7. C 【解析】要使 有意义,
则 ,,
解得:.
故选:C.
8. A
9. C
10. A
【解析】设 ,且 ,
所以 ,
所以 ,
所以 ,
所以 .
第二部分
11.
12.
【解析】由二次根式有意义的条件得 解得 ,代入 得 ,所以 .
13. ,且
【解析】由题意得:,且 ,
解得:,且 .
14.
15.
【解析】 最简二次根式 与 的被开方数相同,
,解得 .
16.
【解析】.
第三部分
17. (1)
(2)
(3)
(4)
18. .
19. 由 ,得 .
所以当 时, 表示二次根式.
20. (1) ;
【解析】由题意得 的一个有理化因式是 ,
.(答案不唯一)
(2)
【解析】
(3) .
21. 设原矩形猪舍共用 长的铁网,则其长、宽分别为 ,,原面积 ,需增加的面积为 .
①设方案一中新增正方形猪舍边长为 ,则 (),所以 ,所以 ,
故采用方案一时,需再买铁网长度为原来猪舍所用铁网总长的 .
②若采用方案二,则改建后的猪舍的面积为 ,
设正方形的边长为 ,则 (),所以 ,所以 ,
故采用方案二时,需要用的铁网与原来猪舍铁网的总长度相等,不需再买铁网.
综上所述,方案二比较好,可以不用再买铁网.
22. (1) 由解题规律可直接写出 .
(2) ,,且 ,
,
.
23. (1)
(2)
24.
25. (1) .
(2) .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2021-2022学年八年级(下)第十六章二次根式检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 下列二次根式中,最简二次根式为
A. B. C. D.
2. 若 化简后的值可以和 合并,则 的值可以是
A. B. C. D.
3. 下列计算错误的是
A. B. C. D.
4. 若 ,则
A. B. C. D.
5. 与 结果相同的是
A. B. C. D.
6. 如图,矩形内有两个相邻的正方形,其面积分别为 和 ,则图中阴影部分的面积为
A. B. C. D.
7. 要使 有意义,则 的取值范围为
A. B. C. D.
8. ,, 三个数的大小关系是
A. B. C. D.
9. 二次根式 的一个有理化因式是
A. B. C. D.
10. 我们可以用平方之后再开方的方式来化简一些有特点的无理数,如:对于 ,设 ,易知 ,故 ,由 ,解得 ,即 .根据以上方法,化简 后的结果为
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 化简: .
12. 若 ,则 .
13. 代数式 在实数范围内有意义,则 的取值范围是 .
14. .
15. 若最简二次根式 与 的被开方数相同,则 .
16. 化简: 的结果是 .
三、解答题(共9小题;共72分)
17. (8分)化简:
(1);
(2);
(3);
(4).
18. (8分)计算:.
19. (8分)实数 在什么范围内取值时,下列各式表示二次根式
.
20. (8分)阅读下面的材料,解答后面提出的问题:
黑白双雄,纵横江湖;双剑合璧,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如:,,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式的除法可以这样解:,.像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.
解决问题:
(1) 的一个有理化因式是 ,将 分母有理化得 .
(2)已知 ,,则 .
(3)利用上面所提供的解法,请化简 .
21.(8分) 现有一个用铁网围成的长、宽之比为 的猪舍,需将面积扩大 ,方案有两种.方案一:再另外单独围一个正方形猪舍;方案二:将原猪舍改成正方形猪舍.你认为哪个方案比较好 为什么
22.(8分) 观察下列一组等式,再解答问题:
,,,,.
(1)利用上面的规律,计算下列式子的值.
.
(2)利用上面的规律,试比较 与 的大小.
23. (8分)计算
(1);
(2)
24. (8分)如图,大正方形边长为 ,去掉一个边长为 的小正方形后,求留下的阴影部分的面积.(保留三个有效数字)
25.(8分) 如图,已知正方形 的面积为 ,正方形 的面积为 .
(1)求矩形 的周长;
(2)求矩形 的面积.
答案
第一部分
1. B
2. C
3. C 【解析】被开方数是带分数的要先化成假分数,再化简,即 .故选项C中的计算错误.
4. C
5. A
6. B 【解析】由题意可得,大正方形的边长为 ,小正方形的边长为 ,
阴影部分的面积为 ,
故选B.
7. C 【解析】要使 有意义,
则 ,,
解得:.
故选:C.
8. A
9. C
10. A
【解析】设 ,且 ,
所以 ,
所以 ,
所以 ,
所以 .
第二部分
11.
12.
【解析】由二次根式有意义的条件得 解得 ,代入 得 ,所以 .
13. ,且
【解析】由题意得:,且 ,
解得:,且 .
14.
15.
【解析】 最简二次根式 与 的被开方数相同,
,解得 .
16.
【解析】.
第三部分
17. (1)
(2)
(3)
(4)
18. .
19. 由 ,得 .
所以当 时, 表示二次根式.
20. (1) ;
【解析】由题意得 的一个有理化因式是 ,
.(答案不唯一)
(2)
【解析】
(3) .
21. 设原矩形猪舍共用 长的铁网,则其长、宽分别为 ,,原面积 ,需增加的面积为 .
①设方案一中新增正方形猪舍边长为 ,则 (),所以 ,所以 ,
故采用方案一时,需再买铁网长度为原来猪舍所用铁网总长的 .
②若采用方案二,则改建后的猪舍的面积为 ,
设正方形的边长为 ,则 (),所以 ,所以 ,
故采用方案二时,需要用的铁网与原来猪舍铁网的总长度相等,不需再买铁网.
综上所述,方案二比较好,可以不用再买铁网.
22. (1) 由解题规律可直接写出 .
(2) ,,且 ,
,
.
23. (1)
(2)
24.
25. (1) .
(2) .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
