1.2.1 直角三角形的性质与判定、互逆命题 课件(共21张PPT)
文档属性
| 名称 | 1.2.1 直角三角形的性质与判定、互逆命题 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 21:41:22 | ||
图片预览







文档简介
(共21张PPT)
2 直角三角形
第1课时 直角三角形的性质与判定、互逆命题
学习目标
1.进一步掌握推理证明的方法,发展演绎推理能力.
2.结合具体例子了解逆命题的概念,会识别两个互逆命题.
旧知回顾
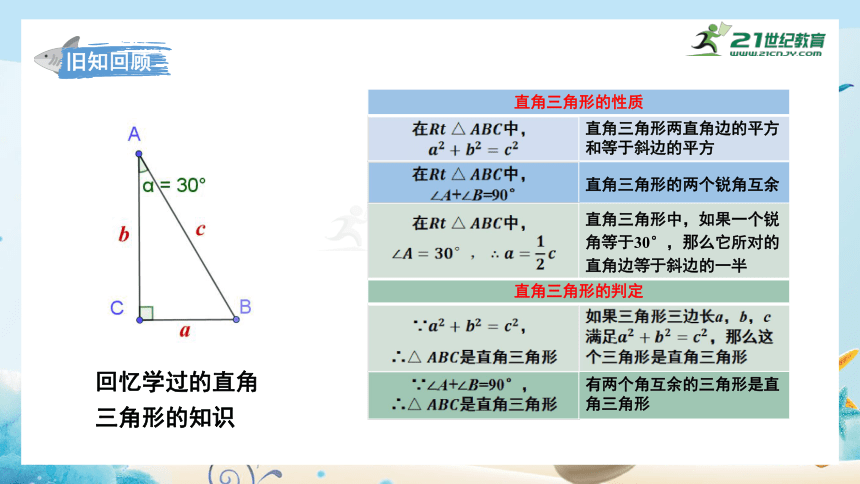
直角三角形定义:
有一个角为90°的三角形是直角三角形.
直角三角形的性质 直角三角形两直角边的平方和等于斜边的平方
直角三角形的判定
有两个角互余的三角形是直角三角形
回忆学过的直角三角形的知识
直角三角形的两个锐角互余
直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
旧知回顾
已知:如图,在Rt△ABC中,∠C=90°.
求证:∠A+∠B=90°
证明:在△ABC中,
∠A+∠B +∠C=180° ,
定理:在直角三角形中,两个锐角互余.
分析:结合条件,Rt△ABC ,可以联想到哪些定理呢?
根据结论∠A+∠B=90°,
联想哪些公式呢?
总结:思考条件、结论相关的定理,结合之前类似的做题经验,推出结论时要注意结构严谨.
∵ ∠C=90°,
∴∠A+∠B=180°-∠C
=180°-90°
=90° .
A
B
C
探究新知
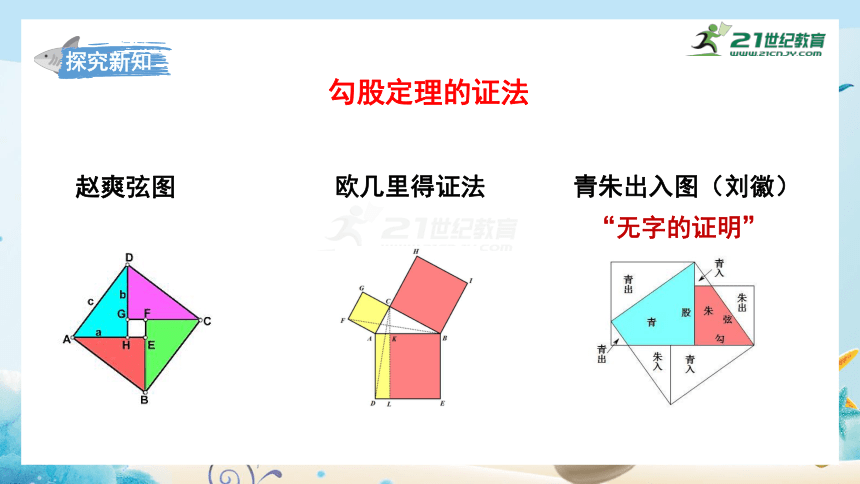
赵爽弦图
勾股定理的证法
欧几里得证法
青朱出入图(刘徽)
“无字的证明”
探究新知
B'
A'
N
C'
M
a
b
勾股定理逆定理:如果三角形三边长a,b,c满足,那么这个三角形是直角三角形.
做完题记得及时总结经验
经典证法
“构造法”
分析:和边有关的定理有哪些呢?怎么证直角呢?
三角形的三边关系,锐角互余,“SSS”证全等,做辅助线构造直角
证明:画一个△A'B'C'中,使∠C'=90 °, B'C'=a, C'A'=b
在Rt△A'B'C'中, A'B'= B'C'2 + C'A'2= a2 + b2
a2 + b2 = c2 =AB2
A'B'2= c2 =AB2
A'B'= c =AB
在△ ABC和Rt△A'B'C'中
∴ △ ABC ≌ △A'B'C’
∴ ∠C =∠C'=90 °
∴ △ ABC是直角三角形
演绎推理
1、结合条件、结论联想相关的定理,或者结合条件联系类似的经验;
2、推理过程要严谨,方法要及时总结.
结合条件(综合法)
分析结论(分析法)
演绎推理
合情推理
猜想,归纳
证明,验证
探索,发现,猜想,证明,是科学研究的必经之路.
特殊到一般
一般到特殊
探究新知
下面两组命题有什么特点?
直角三角形的两个锐角互余;
有两个角互余的三角形是直角三角形;
直角三角形两直角边的平方和等于斜边的平方;
如果三角形三边长a,b,c满足,那么这个三角形是直角三角形.
温故而知新
探究新知
还能举出类似的命题吗
同位角相等, 两直线平行
两直线平行,同位角相等
等边对等角
等角对等边
能归纳它们的特点吗:
条件和结论是“互换” 的
举一而反三
探究新知
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
定义:
如果两个角是对顶角,那么它们相等
如果两个角相等,那么它们是对顶角
假命题
是互逆命题吗?
是互逆命题!
互逆命题中可以有假命题
探究新知
1.“两直线平行,同旁内角互补” ,它的逆命题是_____________________________,这是一个_________.
2.“四边形是多边形” ,它的逆命题是________________,
这是一个___________.
易错提醒:原命题是真命题,它的逆命题不一定是真命题.
多边形是四边形
假命题
同旁内角互补,两直线平行
真命题
做一做
如果一个定理的逆命题经过证明是真命题,那么它也是
一个定理,其中一个定理称为另一个定理的逆定理.
定义:
那么,原命题和逆命题都是真命题的情况就比较特殊了,又该怎么描述呢?
那么,勾股定理和勾股定理逆定理既是_____________,也是_____________.
互逆命题
互逆定理
命题
逆定理
逆命题
互换条件结论
例:如果两三角形全等,那么对应角相等;
如果对应角相等,那么两三角形全等
互换条件结论+是真命题
定理
例:两直线平行,内错角相等;
内错角相等,两直线平行
一定存在,但不一定 “真”
稀有,一定 “真”
假命题
性质
判定
互为
逆定理
互逆定理:
1、直角三角形
2、等腰三角形
3、等边三角形
4、全等三角形
5、平行线
6、角平分线
7、垂直平分线
三个角都相等的三角形是等边三角形;
等边三角形的三个内角都相等
可以尝试用演绎推理证明!
性质定理和判定定理互为逆定理
牢记定理对证明很有帮助
2、合情推理猜结论,演绎推理推结论,
学以致用解问题,反思提升成系统.
1、演绎推理很严谨,公理定理是依据;
互逆命题和定理,有定理时才保真.
几何学习的一般过程
知识
方法
课堂小结
角的性质
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形.
直角三角形
边的性质
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
互逆命题
第一个命题的条件是第二个命题的结论;
第一个命题的结论是第二个命题的条件.
互逆命题与互逆定理
互逆定理
一个定理的逆命题也是定理,这两个定理叫做互逆定理
课堂小结
课后作业
1. 完成学案课后作业习题.
2. 拓展作业:查阅资料,看看勾股定理的证明方法都有哪些,做一张手抄报.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
2 直角三角形
第1课时 直角三角形的性质与判定、互逆命题
学习目标
1.进一步掌握推理证明的方法,发展演绎推理能力.
2.结合具体例子了解逆命题的概念,会识别两个互逆命题.
旧知回顾
直角三角形定义:
有一个角为90°的三角形是直角三角形.
直角三角形的性质 直角三角形两直角边的平方和等于斜边的平方
直角三角形的判定
有两个角互余的三角形是直角三角形
回忆学过的直角三角形的知识
直角三角形的两个锐角互余
直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
旧知回顾
已知:如图,在Rt△ABC中,∠C=90°.
求证:∠A+∠B=90°
证明:在△ABC中,
∠A+∠B +∠C=180° ,
定理:在直角三角形中,两个锐角互余.
分析:结合条件,Rt△ABC ,可以联想到哪些定理呢?
根据结论∠A+∠B=90°,
联想哪些公式呢?
总结:思考条件、结论相关的定理,结合之前类似的做题经验,推出结论时要注意结构严谨.
∵ ∠C=90°,
∴∠A+∠B=180°-∠C
=180°-90°
=90° .
A
B
C
探究新知
赵爽弦图
勾股定理的证法
欧几里得证法
青朱出入图(刘徽)
“无字的证明”
探究新知
B'
A'
N
C'
M
a
b
勾股定理逆定理:如果三角形三边长a,b,c满足,那么这个三角形是直角三角形.
做完题记得及时总结经验
经典证法
“构造法”
分析:和边有关的定理有哪些呢?怎么证直角呢?
三角形的三边关系,锐角互余,“SSS”证全等,做辅助线构造直角
证明:画一个△A'B'C'中,使∠C'=90 °, B'C'=a, C'A'=b
在Rt△A'B'C'中, A'B'= B'C'2 + C'A'2= a2 + b2
a2 + b2 = c2 =AB2
A'B'2= c2 =AB2
A'B'= c =AB
在△ ABC和Rt△A'B'C'中
∴ △ ABC ≌ △A'B'C’
∴ ∠C =∠C'=90 °
∴ △ ABC是直角三角形
演绎推理
1、结合条件、结论联想相关的定理,或者结合条件联系类似的经验;
2、推理过程要严谨,方法要及时总结.
结合条件(综合法)
分析结论(分析法)
演绎推理
合情推理
猜想,归纳
证明,验证
探索,发现,猜想,证明,是科学研究的必经之路.
特殊到一般
一般到特殊
探究新知
下面两组命题有什么特点?
直角三角形的两个锐角互余;
有两个角互余的三角形是直角三角形;
直角三角形两直角边的平方和等于斜边的平方;
如果三角形三边长a,b,c满足,那么这个三角形是直角三角形.
温故而知新
探究新知
还能举出类似的命题吗
同位角相等, 两直线平行
两直线平行,同位角相等
等边对等角
等角对等边
能归纳它们的特点吗:
条件和结论是“互换” 的
举一而反三
探究新知
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
定义:
如果两个角是对顶角,那么它们相等
如果两个角相等,那么它们是对顶角
假命题
是互逆命题吗?
是互逆命题!
互逆命题中可以有假命题
探究新知
1.“两直线平行,同旁内角互补” ,它的逆命题是_____________________________,这是一个_________.
2.“四边形是多边形” ,它的逆命题是________________,
这是一个___________.
易错提醒:原命题是真命题,它的逆命题不一定是真命题.
多边形是四边形
假命题
同旁内角互补,两直线平行
真命题
做一做
如果一个定理的逆命题经过证明是真命题,那么它也是
一个定理,其中一个定理称为另一个定理的逆定理.
定义:
那么,原命题和逆命题都是真命题的情况就比较特殊了,又该怎么描述呢?
那么,勾股定理和勾股定理逆定理既是_____________,也是_____________.
互逆命题
互逆定理
命题
逆定理
逆命题
互换条件结论
例:如果两三角形全等,那么对应角相等;
如果对应角相等,那么两三角形全等
互换条件结论+是真命题
定理
例:两直线平行,内错角相等;
内错角相等,两直线平行
一定存在,但不一定 “真”
稀有,一定 “真”
假命题
性质
判定
互为
逆定理
互逆定理:
1、直角三角形
2、等腰三角形
3、等边三角形
4、全等三角形
5、平行线
6、角平分线
7、垂直平分线
三个角都相等的三角形是等边三角形;
等边三角形的三个内角都相等
可以尝试用演绎推理证明!
性质定理和判定定理互为逆定理
牢记定理对证明很有帮助
2、合情推理猜结论,演绎推理推结论,
学以致用解问题,反思提升成系统.
1、演绎推理很严谨,公理定理是依据;
互逆命题和定理,有定理时才保真.
几何学习的一般过程
知识
方法
课堂小结
角的性质
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形.
直角三角形
边的性质
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
互逆命题
第一个命题的条件是第二个命题的结论;
第一个命题的结论是第二个命题的条件.
互逆命题与互逆定理
互逆定理
一个定理的逆命题也是定理,这两个定理叫做互逆定理
课堂小结
课后作业
1. 完成学案课后作业习题.
2. 拓展作业:查阅资料,看看勾股定理的证明方法都有哪些,做一张手抄报.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
