1.1.4 等边三角形的判定与含30°角的直角三角形的性质 课件(共29张PPT)
文档属性
| 名称 | 1.1.4 等边三角形的判定与含30°角的直角三角形的性质 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 21:38:43 | ||
图片预览







文档简介
(共29张PPT)
1 等腰三角形
第4课时 等边三角形的判定与含30°角的直角三角形的性质
1.能够证明等边三角形的判断方法及含30°直角三角形性质;感受几何语言的魅力;
2.能够运用上述三个定理解决问题.
学习目标
情境引入
情境引入
情境引入
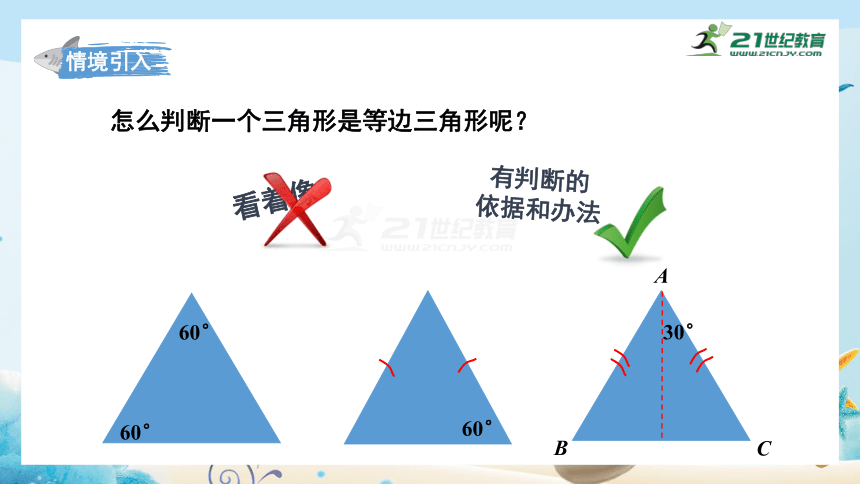
看着像
60°
60°
60°
A
B
C
30°
有判断的
依据和办法
怎么判断一个三角形是等边三角形呢?
情境引入
探究新知
三边都相等的三角形是
等边三角形.
你有其它判断等边三角形的方法吗?
三角形的基本元素是“边”和“角”
思考方向:
角
______________的三角形是等边三角形.
探究新知
要探究判断方法,可以反思性质.
等边三角形的三个内角都相等,并且每个角都是60°.
三个角都相等
______________的三角形是等边三角形.
三个角都相等
命题证明:明确条件和结论=>画出图形=>书写证明过程.
探究新知
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC为等边三角形.
A
B
C
求证:三个角都相等的三角形是等边三角形.
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC为等边三角形.
A
B
C
证明:∵∠A=∠B
∴AC=BC
∵∠B=∠C.
∴AB=AC
∴AB=AC=BC
∴△ABC为等边三角形.
定理:
做一做
判断并说明理由:
1.有2个角是60°的三角形是等边三角形.( )
2.△ABC是等边三角形,作DE∥BC ,那么△ADE也是等边三角形. ( )
A
B
C
D
E
做一做
判断并说明理由:
3. △ABC是等边三角形,如果过它的三个顶点作对边的平行线得到一个新的△DEF,那么△DEF也是等边三角形. ( )
A
B
C
D
E
F
探究新知
等边三角形是特殊的等腰三角形.
特殊在哪儿?
的 三角形是等边三角形.
等
腰
三角形的基本元素是“边”和“角”.
思考方向
要探究判断方法,可以反思性质.
有 个角等于60°的等腰三角形是等边三角形.
一
探究新知
求证:有一个角等于60°的等腰三角形是等边三角形.
顶角
底角
分类讨论:
当顶角是60°时;
当底角是60°时。
探究新知
180-60
2
已知:△ABC中,AB=AC,且有一个角为60°.
求证:等腰△ABC为等边三角形.
A
B
C
∵AB=AC
∴∠B=∠C
∵∠A=60°
∴∠B=∠C=60°
∴∠B=∠C=∠A
∴等腰△ABC为等边三角形.
证明:①当∠A=60°时
60°
A
B
C
180-60
2
求证:有一个角等于60°的等腰三角形是等边三角形.
已知:△ABC中,AB=AC,且有一个角为60°.
求证:等腰△ABC为等边三角形.
∵AB=AC
∴∠B=∠C
∵∠A=60°
∴∠B=∠C=60°
∴∠B=∠C=∠A
∴等腰△ABC为等边三角形.
证明:①当∠A=60°时
求证:有一个角等于60°的等腰三角形是等边三角形.
A
B
C
∵AB=AC,∠B=60°
∴∠C=∠B=60°
∴∠A=60°
∴∠B=∠C=∠A
∴等腰△ABC为等边三角形.
60°
60°
180-60×2
②当∠B=60°(或∠C=60°)时.
定理:
做一做
如图,将矩形ABCD一个角沿AE折叠,使得∠BAE=30°,点B落在B’处,连接BB’ ,判断△ABB’的形状,并说明理由.
A
B
C
D
E
B’
30°
30°
先目测,再推理
探究:30°所对的直角边与斜边的关系。
30°
探究新知
等边三角形
探究:30°所对的直角边与斜边的关系。
探究新知
a
2a
2a
等边三角形
探究:30°所对的直角边与斜边的关系。
探究新知
A
B
C
D
已知:如图,△ABC是直角三角形,∠C=90°,∠A=30°.
求证:BC=AB.
证明:如图,延长BC至点D,使CD=BC,连接AD.
∵∠ACB=90°,∠BAC=30°
∴∠ACD=90°,∠B=60°
∵AC=AC
∴△ABC≌△ACD(SAS)
∴AB=AD
∴△ABD等边三角形
∴BC=AB.
构造全等
定理 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
如图,在Rt△ABC中,
∵∠A=30°
∴BC=AB.
A
B
C
探究新知
典型例题
求证:如果等腰三角形的底角为15°,那么腰上的高是腰长的一半.
例题
已知:如图,在△ABC中,AB=AC,∠B=15°,CD是腰上的高.
求证:CD=AB.
A
B
C
D
证明:在△ABC中,AB=AC,∠B=15°
∴∠ACB=∠B=15°
∴∠DAC=∠B+∠ACB=15°+15°=30°
∵CD是腰上的高,∴∠ADC=90°
∴CD=AC.
∴CD=AB.
课堂小结
三个角都相等的三角形是等边三角形.
定理一
有一个角等于60°的等腰三角形是等边三角形.
定理二
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
定理三
三角形
角
线
等腰三角形
等边三角形
判定
全等三角形
性质
轴对称
含30°角的直角三角形
边
思考
方向
课堂小结
课后作业
1. 完成学案课后作业习题.
2. 拓展作业:反思第一节这四堂课以来的学习内容,根据第一节等腰三角形的内容制作思维导图.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1 等腰三角形
第4课时 等边三角形的判定与含30°角的直角三角形的性质
1.能够证明等边三角形的判断方法及含30°直角三角形性质;感受几何语言的魅力;
2.能够运用上述三个定理解决问题.
学习目标
情境引入
情境引入
情境引入
看着像
60°
60°
60°
A
B
C
30°
有判断的
依据和办法
怎么判断一个三角形是等边三角形呢?
情境引入
探究新知
三边都相等的三角形是
等边三角形.
你有其它判断等边三角形的方法吗?
三角形的基本元素是“边”和“角”
思考方向:
角
______________的三角形是等边三角形.
探究新知
要探究判断方法,可以反思性质.
等边三角形的三个内角都相等,并且每个角都是60°.
三个角都相等
______________的三角形是等边三角形.
三个角都相等
命题证明:明确条件和结论=>画出图形=>书写证明过程.
探究新知
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC为等边三角形.
A
B
C
求证:三个角都相等的三角形是等边三角形.
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC为等边三角形.
A
B
C
证明:∵∠A=∠B
∴AC=BC
∵∠B=∠C.
∴AB=AC
∴AB=AC=BC
∴△ABC为等边三角形.
定理:
做一做
判断并说明理由:
1.有2个角是60°的三角形是等边三角形.( )
2.△ABC是等边三角形,作DE∥BC ,那么△ADE也是等边三角形. ( )
A
B
C
D
E
做一做
判断并说明理由:
3. △ABC是等边三角形,如果过它的三个顶点作对边的平行线得到一个新的△DEF,那么△DEF也是等边三角形. ( )
A
B
C
D
E
F
探究新知
等边三角形是特殊的等腰三角形.
特殊在哪儿?
的 三角形是等边三角形.
等
腰
三角形的基本元素是“边”和“角”.
思考方向
要探究判断方法,可以反思性质.
有 个角等于60°的等腰三角形是等边三角形.
一
探究新知
求证:有一个角等于60°的等腰三角形是等边三角形.
顶角
底角
分类讨论:
当顶角是60°时;
当底角是60°时。
探究新知
180-60
2
已知:△ABC中,AB=AC,且有一个角为60°.
求证:等腰△ABC为等边三角形.
A
B
C
∵AB=AC
∴∠B=∠C
∵∠A=60°
∴∠B=∠C=60°
∴∠B=∠C=∠A
∴等腰△ABC为等边三角形.
证明:①当∠A=60°时
60°
A
B
C
180-60
2
求证:有一个角等于60°的等腰三角形是等边三角形.
已知:△ABC中,AB=AC,且有一个角为60°.
求证:等腰△ABC为等边三角形.
∵AB=AC
∴∠B=∠C
∵∠A=60°
∴∠B=∠C=60°
∴∠B=∠C=∠A
∴等腰△ABC为等边三角形.
证明:①当∠A=60°时
求证:有一个角等于60°的等腰三角形是等边三角形.
A
B
C
∵AB=AC,∠B=60°
∴∠C=∠B=60°
∴∠A=60°
∴∠B=∠C=∠A
∴等腰△ABC为等边三角形.
60°
60°
180-60×2
②当∠B=60°(或∠C=60°)时.
定理:
做一做
如图,将矩形ABCD一个角沿AE折叠,使得∠BAE=30°,点B落在B’处,连接BB’ ,判断△ABB’的形状,并说明理由.
A
B
C
D
E
B’
30°
30°
先目测,再推理
探究:30°所对的直角边与斜边的关系。
30°
探究新知
等边三角形
探究:30°所对的直角边与斜边的关系。
探究新知
a
2a
2a
等边三角形
探究:30°所对的直角边与斜边的关系。
探究新知
A
B
C
D
已知:如图,△ABC是直角三角形,∠C=90°,∠A=30°.
求证:BC=AB.
证明:如图,延长BC至点D,使CD=BC,连接AD.
∵∠ACB=90°,∠BAC=30°
∴∠ACD=90°,∠B=60°
∵AC=AC
∴△ABC≌△ACD(SAS)
∴AB=AD
∴△ABD等边三角形
∴BC=AB.
构造全等
定理 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
如图,在Rt△ABC中,
∵∠A=30°
∴BC=AB.
A
B
C
探究新知
典型例题
求证:如果等腰三角形的底角为15°,那么腰上的高是腰长的一半.
例题
已知:如图,在△ABC中,AB=AC,∠B=15°,CD是腰上的高.
求证:CD=AB.
A
B
C
D
证明:在△ABC中,AB=AC,∠B=15°
∴∠ACB=∠B=15°
∴∠DAC=∠B+∠ACB=15°+15°=30°
∵CD是腰上的高,∴∠ADC=90°
∴CD=AC.
∴CD=AB.
课堂小结
三个角都相等的三角形是等边三角形.
定理一
有一个角等于60°的等腰三角形是等边三角形.
定理二
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
定理三
三角形
角
线
等腰三角形
等边三角形
判定
全等三角形
性质
轴对称
含30°角的直角三角形
边
思考
方向
课堂小结
课后作业
1. 完成学案课后作业习题.
2. 拓展作业:反思第一节这四堂课以来的学习内容,根据第一节等腰三角形的内容制作思维导图.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
