1.2.2 直角三角形全等的判定 课件(共22张PPT)
文档属性
| 名称 | 1.2.2 直角三角形全等的判定 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-14 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
2 直角三角形
第2课时 直角三角形全等的判定
学习目标
1.根据已知条件运用尺规作出规范图形.
2.经历探索、猜测、证明的过程,能够证明直角三角形全等“HL”判定定理.
3.会熟练应用“HL”解决相关的实际问题.
旧知回顾
一般三角形全等的判定方法:
公理
SSS:三边分别相等的两个三角形全等.
SAS:两边及其夹角分别相等的两个三角形全等.
ASA:两角及其夹边分别相等的两个三角形全等.
AAS:两角及其中一角的对边对应相等的两个三角形全等 .
推论
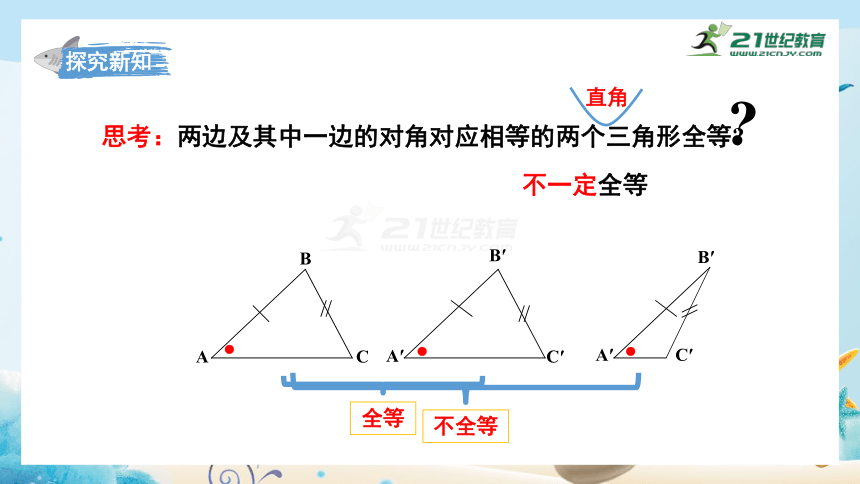
思考:两边及其中一边的对角对应相等的两个三角形全等
思考:两边及其中一边的对角对应相等的两个三角形全等
探究新知
不一定全等
A
B
C
A′
B′
C′
A′
B′
C′
●
●
●
全等
不全等
直角
尺规作图:
利用尺规作一个RtΔABC,∠C=90°,AB=5cm,CB=3cm.
依照步骤做一做:
(1)作∠MCN=90°;
(2)在射线CM上截取线段CB=3cm;
(3)以B为圆心,5cm为半径画弧,交射线CN于点A;
(4)连接AB.
猜想:两边及其中一边的对角对应相等的两个直角三角形全等.
思考:两边及其中一边的对角对应相等的两个三角形全等
直角
A
B
C
A′
B′
C′
已知:如图,在△ABC和△A′B′C′中,
AC=A′C ′,AB=A′B′,
∠C=∠C′=90°.
求证:△ABC≌△A′B′C′.
猜想:斜边和一条直角边分别相等的两个直角三角形全等.
可借助优教平台的“【探究动画】练习——三角形全等的判定HL”互动资源,动态、直观、辅助探究与发现.
证明:在△ABC中,
∵∠C=90°,∴BC2=AB2-AC2(勾股定理).
同理,B′C′2=A′B′2-A′C′2 .
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′(SSS).
A
B
C
A′
B′
C′
已知:如图,在△ABC和△A′B′C′中,
AC=A′C ′,AB=A′B′,
∠C=∠C′=90°.
求证:△ABC≌△A′B′C′.
猜想:斜边和一条直角边分别相等的两个直角三角形全等.
定理:
简称“HL”判定定理
A
B
C
A′
B′
C′
如图,在△ABC和△A′B′C′中,
∵AC=A′C ′,AB=A′B′,
∠C=∠C′=90°.
∴△ABC≌△A′B′C′.
一般三角形全等的判定 SSS SAS ASA AAS
直角三角形全等的判定 SSS SAS ASA AAS HL
灵活运用各种方法证明直角三角形全等
小结:
满足下列条件的两个三角形是否全等 为什么
(1)一个锐角及这个锐角的对边对应相等的两个直角三角形;
(2)一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形;
(3)两直角边对应相等的两个直角三角形;
(4)有两边对应相等的两个直角三角形.
做一做
满足下列条件的两个三角形是否全等 为什么
(1)一个锐角及这个锐角的对边对应相等的两个直角三角形;
做一做
全等 (AAS)
满足下列条件的两个三角形是否全等 为什么
(2)一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形;
做一做
全等 (ASA)
满足下列条件的两个三角形是否全等 为什么
(3)两直角边对应相等的两个直角三角形;
做一做
全等 (SAS)
满足下列条件的两个三角形是否全等 为什么
(4)有两边对应相等的两个直角三角形.
做一做
情况1:全等 (SAS)
情况2:全等 (HL)
典型例题
例 1 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:根据题意,可知∠BAC= ∠EDF=90°,
∴Rt△BAC≌Rt△EDF(HL),
∴∠B=∠DEF(全等三角形的对应角相等),
∵∠DEF+∠F=90°(直角三角形的两锐角互余),
∴∠B+∠F=90°.
1. 如图,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,还需要什么条件 把它们分别写出来.
跟踪训练
从添加角来说,可以添加∠CBA=∠DAB或∠CAB=∠DBA;
从添加边来说,可以是AC=BD,也可以是BC=AD.
2. 已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证:△ABC≌△BAD.
跟踪训练
AB=BA
BC=AD
HL
3. 如图,在△ABC≌△A'B'C'中,CD,C'D'分别分别是高,且AC=A'C',CD=C'D',∠ACB=∠A'C'B'.
求证:△ABC≌△A'B'C'.
跟踪训练
直角三角形全等的判定定理 SSS SAS ASA AAS HL
课堂小结
归纳:
两边对应相等的两个直角三角形全等.
一边及一个锐角对应相等的两个直角三角形全等.
注意:两边及其中一边的对角对应相等的两个三角形不一定全等.
课后作业
1. 完成学案课后作业习题.
2. 拓展作业:梳理三角形全等的判定定理,画出对应图形,做出知识导图.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
2 直角三角形
第2课时 直角三角形全等的判定
学习目标
1.根据已知条件运用尺规作出规范图形.
2.经历探索、猜测、证明的过程,能够证明直角三角形全等“HL”判定定理.
3.会熟练应用“HL”解决相关的实际问题.
旧知回顾
一般三角形全等的判定方法:
公理
SSS:三边分别相等的两个三角形全等.
SAS:两边及其夹角分别相等的两个三角形全等.
ASA:两角及其夹边分别相等的两个三角形全等.
AAS:两角及其中一角的对边对应相等的两个三角形全等 .
推论
思考:两边及其中一边的对角对应相等的两个三角形全等
思考:两边及其中一边的对角对应相等的两个三角形全等
探究新知
不一定全等
A
B
C
A′
B′
C′
A′
B′
C′
●
●
●
全等
不全等
直角
尺规作图:
利用尺规作一个RtΔABC,∠C=90°,AB=5cm,CB=3cm.
依照步骤做一做:
(1)作∠MCN=90°;
(2)在射线CM上截取线段CB=3cm;
(3)以B为圆心,5cm为半径画弧,交射线CN于点A;
(4)连接AB.
猜想:两边及其中一边的对角对应相等的两个直角三角形全等.
思考:两边及其中一边的对角对应相等的两个三角形全等
直角
A
B
C
A′
B′
C′
已知:如图,在△ABC和△A′B′C′中,
AC=A′C ′,AB=A′B′,
∠C=∠C′=90°.
求证:△ABC≌△A′B′C′.
猜想:斜边和一条直角边分别相等的两个直角三角形全等.
可借助优教平台的“【探究动画】练习——三角形全等的判定HL”互动资源,动态、直观、辅助探究与发现.
证明:在△ABC中,
∵∠C=90°,∴BC2=AB2-AC2(勾股定理).
同理,B′C′2=A′B′2-A′C′2 .
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′(SSS).
A
B
C
A′
B′
C′
已知:如图,在△ABC和△A′B′C′中,
AC=A′C ′,AB=A′B′,
∠C=∠C′=90°.
求证:△ABC≌△A′B′C′.
猜想:斜边和一条直角边分别相等的两个直角三角形全等.
定理:
简称“HL”判定定理
A
B
C
A′
B′
C′
如图,在△ABC和△A′B′C′中,
∵AC=A′C ′,AB=A′B′,
∠C=∠C′=90°.
∴△ABC≌△A′B′C′.
一般三角形全等的判定 SSS SAS ASA AAS
直角三角形全等的判定 SSS SAS ASA AAS HL
灵活运用各种方法证明直角三角形全等
小结:
满足下列条件的两个三角形是否全等 为什么
(1)一个锐角及这个锐角的对边对应相等的两个直角三角形;
(2)一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形;
(3)两直角边对应相等的两个直角三角形;
(4)有两边对应相等的两个直角三角形.
做一做
满足下列条件的两个三角形是否全等 为什么
(1)一个锐角及这个锐角的对边对应相等的两个直角三角形;
做一做
全等 (AAS)
满足下列条件的两个三角形是否全等 为什么
(2)一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形;
做一做
全等 (ASA)
满足下列条件的两个三角形是否全等 为什么
(3)两直角边对应相等的两个直角三角形;
做一做
全等 (SAS)
满足下列条件的两个三角形是否全等 为什么
(4)有两边对应相等的两个直角三角形.
做一做
情况1:全等 (SAS)
情况2:全等 (HL)
典型例题
例 1 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:根据题意,可知∠BAC= ∠EDF=90°,
∴Rt△BAC≌Rt△EDF(HL),
∴∠B=∠DEF(全等三角形的对应角相等),
∵∠DEF+∠F=90°(直角三角形的两锐角互余),
∴∠B+∠F=90°.
1. 如图,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,还需要什么条件 把它们分别写出来.
跟踪训练
从添加角来说,可以添加∠CBA=∠DAB或∠CAB=∠DBA;
从添加边来说,可以是AC=BD,也可以是BC=AD.
2. 已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证:△ABC≌△BAD.
跟踪训练
AB=BA
BC=AD
HL
3. 如图,在△ABC≌△A'B'C'中,CD,C'D'分别分别是高,且AC=A'C',CD=C'D',∠ACB=∠A'C'B'.
求证:△ABC≌△A'B'C'.
跟踪训练
直角三角形全等的判定定理 SSS SAS ASA AAS HL
课堂小结
归纳:
两边对应相等的两个直角三角形全等.
一边及一个锐角对应相等的两个直角三角形全等.
注意:两边及其中一边的对角对应相等的两个三角形不一定全等.
课后作业
1. 完成学案课后作业习题.
2. 拓展作业:梳理三角形全等的判定定理,画出对应图形,做出知识导图.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
