湘教版数学七年级下册 1.3 .2解决所列方程组中x、y系数不为1形式的实际问题 课件(共35张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 1.3 .2解决所列方程组中x、y系数不为1形式的实际问题 课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-15 11:39:32 | ||
图片预览








文档简介
(共35张PPT)
学习目标
1.学会运用二元一次方程组解决较复杂的实际问题;(重点、难点)
2.进一步经历和体验方程组解决实际问题的过程.
导入新课
生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
情景引入
列方程解决行程问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
讲授新课
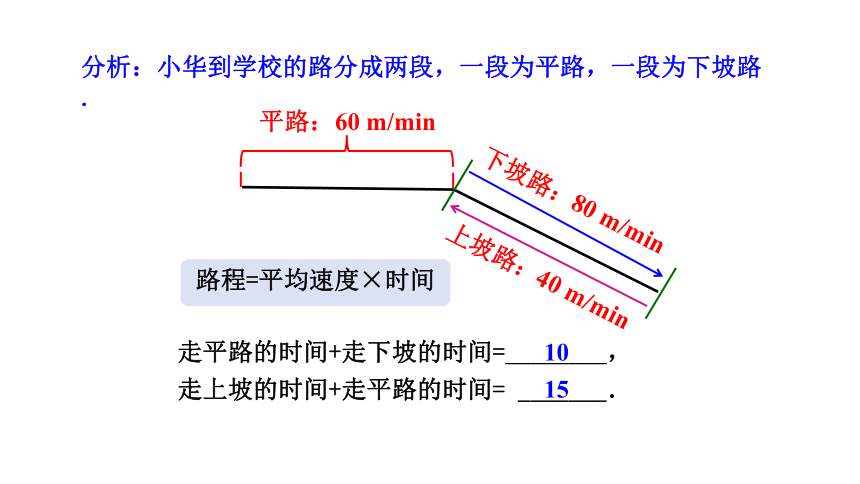
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡的时间=________,
走上坡的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
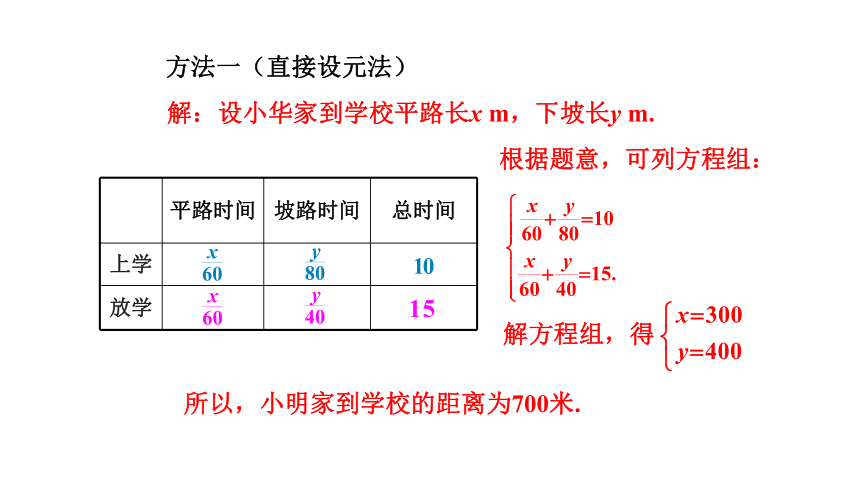
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
方法二(间接设元法)
平路距离 坡路距离
上学
放学
解:设小华下坡路所花时间为x min,上坡路所花时间为y min.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
故 平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
例1 甲、乙两地相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
典例精析
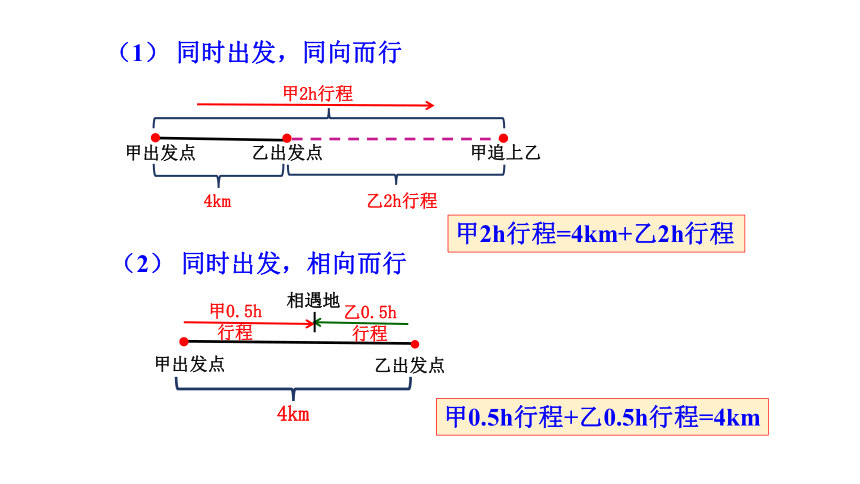
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
解:设甲、乙的速度分别为x km/h, y km/h.根据题意与分析中图示的两个相等关系,得
解方程组,得
答:甲的速度为5 km/h,乙的速度为3 km/h.
我国的长江由西至东奔腾不息,其中九江东至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/小时,
长江水的平均流速为y千米/小时.
答:轮船在静水中的速度为47.5千米/小时,
长江水的平均流速为2.5千米/小时.
练一练
例2:某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
甲说:“我乘这种出租车走了11km,付了17元.”
乙说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
起步价 超过3km后的费用 合计费用
甲
乙
x
x
(11-3)y
(23-3)y
17
35
例3 如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
·
长青化工厂
A
B
铁路120千米
铁路110千米
公路10千米
公路20千米
列方程组解决较复杂的实际问题
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
总结归纳
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
练一练
解:设甲、乙两种货车每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735.
例4. 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
作物品种 种植面积/hm2 需要人数 投入资金/万元
蔬菜 x 5x 1.5x
荞麦 y 4y y
合计 ----- 18 5
将题中出现的量在表格中呈现
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
解方程组,得:
故,承包田地的面积为: x+y=4 hm2
人员安排为为: 5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示.有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用.
运费表
单位:(元/台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
练一练
解:设从北京运往武汉x台,运往重庆(10-x)台,
设从上海运往武汉y台,运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
运费表
单位:(元/台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
例5 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
1. 某星期日,七年级与八年级分别有20,30人去颐和园参观,有30,15人去圆明园参观.七年级买门票花去450元,八年级买门票花去525元.试问:颐和园和圆明园的门票各多少元?
解:设颐和园门票为x元,园明园门票为y元,
根据等量关系得
解这个方程组得
答:颐和园门票为15元,园明园门票为5元.
当堂练习
2.王先生家厨房需更换地面瓷砖,他采用两种颜色的砖搭配使用,其中彩色地砖24元/块,单色地砖12元/块,购买的单色地砖数比彩色地砖数的2倍少15块,买两种地砖共花去2220元.求购买的彩色地砖数和单色地砖数.
解:设购买的彩色地砖数为x块,购买的单色地砖数为y块.
根据等量关系得
解这个方程组得
答:购买彩色地砖数为50块,购买单色地砖数为85块.
3. 某装订车间的工人要将一批书打包后送往邮局,其中每包书的数目相等.第一次他们领来这批书的 ,结果打了14个包还多35本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了11包. 那么这批书共有多少本?
解: 设这批书共有x本,每包书有y本.
根据等量关系得
解这个方程组得
答:这批书共有1500本.
隔壁听到人分银,
不知人数不知银。
每人五两多六两,
每人六两少五两。
多少人数多少银?
解:设有x个人,y两银,
由题意得:
5x+6=y
6x-5=y
4.古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得:
x=11
y=61
5.李大叔销售牛肉干,已知甲客户购买了12包五香味的和10包原味的共花了146元,乙客户购买了6包五香的和8包原味的共花了88元
(1)现在老师带了200元,能否买到10包五香牛肉干和20包原味牛肉干?
解:设五香味每包x元,原味每包y元.
依题意,可列方程组:
解方程组,得
所以老师带200元能买到所需牛肉干.
解:设刚好买五香味x包,原味y包.
(2)现在老师想刚好用完这200元钱,
你能想出哪些牛肉干的包数组合形式?
因为x,y为非负整数
5. 汽车在上坡时速度为28km/h,下坡时速度42km/h,从甲地到乙地用了4小时30分,返回时用了4小时40分,从甲地到乙地上、下坡路各是多少千米?(只列方程组)
知识拓展
分析:从甲地到乙地的上坡路和下坡路分别是从乙地到甲地的下坡路和上坡路.
解:设从甲地到乙地上坡路是x千米,下坡路是y千米.
依题意得
6.有大小两个两位数,在大数的右边写上一个0之后再写上小的数,得到一个五位数;在小数的右边写上大数,然后再写上一个0,也得到一个五位数,第一个五位数除以第二个五位数得到的商为2,余数为590.此外,二倍大数与三倍小数的和是72,求这两个两位数.
解:设大的两位数是x,小的两位数是y,则第一个
五位数是1000x+y,第二个五位数是1000y+10x,
由题意,得
解得
答:这两个两位数分别为21和10.
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
课堂小结
2.这种处理问题的过程可以进一步概括为:
问题
分析
抽象
方程(组)
求解
检验
解答
学习目标
1.学会运用二元一次方程组解决较复杂的实际问题;(重点、难点)
2.进一步经历和体验方程组解决实际问题的过程.
导入新课
生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
情景引入
列方程解决行程问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
讲授新课
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡的时间=________,
走上坡的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
方法二(间接设元法)
平路距离 坡路距离
上学
放学
解:设小华下坡路所花时间为x min,上坡路所花时间为y min.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
故 平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
例1 甲、乙两地相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
典例精析
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
解:设甲、乙的速度分别为x km/h, y km/h.根据题意与分析中图示的两个相等关系,得
解方程组,得
答:甲的速度为5 km/h,乙的速度为3 km/h.
我国的长江由西至东奔腾不息,其中九江东至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/小时,
长江水的平均流速为y千米/小时.
答:轮船在静水中的速度为47.5千米/小时,
长江水的平均流速为2.5千米/小时.
练一练
例2:某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
甲说:“我乘这种出租车走了11km,付了17元.”
乙说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
起步价 超过3km后的费用 合计费用
甲
乙
x
x
(11-3)y
(23-3)y
17
35
例3 如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
·
长青化工厂
A
B
铁路120千米
铁路110千米
公路10千米
公路20千米
列方程组解决较复杂的实际问题
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
总结归纳
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
练一练
解:设甲、乙两种货车每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735.
例4. 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
作物品种 种植面积/hm2 需要人数 投入资金/万元
蔬菜 x 5x 1.5x
荞麦 y 4y y
合计 ----- 18 5
将题中出现的量在表格中呈现
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
解方程组,得:
故,承包田地的面积为: x+y=4 hm2
人员安排为为: 5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示.有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用.
运费表
单位:(元/台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
练一练
解:设从北京运往武汉x台,运往重庆(10-x)台,
设从上海运往武汉y台,运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
运费表
单位:(元/台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
例5 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
1. 某星期日,七年级与八年级分别有20,30人去颐和园参观,有30,15人去圆明园参观.七年级买门票花去450元,八年级买门票花去525元.试问:颐和园和圆明园的门票各多少元?
解:设颐和园门票为x元,园明园门票为y元,
根据等量关系得
解这个方程组得
答:颐和园门票为15元,园明园门票为5元.
当堂练习
2.王先生家厨房需更换地面瓷砖,他采用两种颜色的砖搭配使用,其中彩色地砖24元/块,单色地砖12元/块,购买的单色地砖数比彩色地砖数的2倍少15块,买两种地砖共花去2220元.求购买的彩色地砖数和单色地砖数.
解:设购买的彩色地砖数为x块,购买的单色地砖数为y块.
根据等量关系得
解这个方程组得
答:购买彩色地砖数为50块,购买单色地砖数为85块.
3. 某装订车间的工人要将一批书打包后送往邮局,其中每包书的数目相等.第一次他们领来这批书的 ,结果打了14个包还多35本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了11包. 那么这批书共有多少本?
解: 设这批书共有x本,每包书有y本.
根据等量关系得
解这个方程组得
答:这批书共有1500本.
隔壁听到人分银,
不知人数不知银。
每人五两多六两,
每人六两少五两。
多少人数多少银?
解:设有x个人,y两银,
由题意得:
5x+6=y
6x-5=y
4.古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得:
x=11
y=61
5.李大叔销售牛肉干,已知甲客户购买了12包五香味的和10包原味的共花了146元,乙客户购买了6包五香的和8包原味的共花了88元
(1)现在老师带了200元,能否买到10包五香牛肉干和20包原味牛肉干?
解:设五香味每包x元,原味每包y元.
依题意,可列方程组:
解方程组,得
所以老师带200元能买到所需牛肉干.
解:设刚好买五香味x包,原味y包.
(2)现在老师想刚好用完这200元钱,
你能想出哪些牛肉干的包数组合形式?
因为x,y为非负整数
5. 汽车在上坡时速度为28km/h,下坡时速度42km/h,从甲地到乙地用了4小时30分,返回时用了4小时40分,从甲地到乙地上、下坡路各是多少千米?(只列方程组)
知识拓展
分析:从甲地到乙地的上坡路和下坡路分别是从乙地到甲地的下坡路和上坡路.
解:设从甲地到乙地上坡路是x千米,下坡路是y千米.
依题意得
6.有大小两个两位数,在大数的右边写上一个0之后再写上小的数,得到一个五位数;在小数的右边写上大数,然后再写上一个0,也得到一个五位数,第一个五位数除以第二个五位数得到的商为2,余数为590.此外,二倍大数与三倍小数的和是72,求这两个两位数.
解:设大的两位数是x,小的两位数是y,则第一个
五位数是1000x+y,第二个五位数是1000y+10x,
由题意,得
解得
答:这两个两位数分别为21和10.
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
课堂小结
2.这种处理问题的过程可以进一步概括为:
问题
分析
抽象
方程(组)
求解
检验
解答
